В работе изучается статистическое взаимодействие параллелных цилиндрических труб с грунтом.
In this calculation parallel cylindrical pumps’ and sand’s effect to each other is learned.
При определении давления грунта на трубы необходимо учитывать такие факторы, как количество ниток, рельеф насыпи, условия опирания труб и другие факторы, встречающиеся в проектной практике.
В качестве расчетной модели принимается весомая упругая среда, содержащая подкрепленные круговыми цилиндрами отверстия и другие включения. На внешнем контакте трубы со средой краевые условия имеют следующий вид:
‒ на вертикальных границах сдвигающие напряжения, горизонтальные перемещения либо равны нулю, либо эти границы свободные;
‒ на нижней горизонтальной границе, примыкающей к основанию насыпи, отсутствуют вертикальные и горизонтальные перемещения;
‒ верхняя поверхность либо свободна от внешних воздействий, либо загружена поверхностной нагрузкой.
Разбивку выбранной расчетной области проводим в виде тетраэдральных конечных элементов. При этом разбивочная сетка должна сгущаться по мере приближения к трубе, так как именно вокруг труб возникает наибольшая концентрация давления грунта. На основе метода конечных элементов разработан алгоритм и составлена программа на языке Фортран.
При оценке сходимости полученного приближенного решения, соответствующего данной разбивке, для точного решения необходимо производить более мелкую разбивку расчетной области. Затем следует провести сравнение решений, соответствующих обеим разбивкам. Если они отличаются друг от друга на величину, большую наперед заданной точности вычислений, то необходимо сделать еще более мелкую третью разбивку области и соответствующее ей решение сравнить с решением для второй разбивки и т. д.
Следует отметить, что при плотном расположении труб в местах их со- прикасания возникают “особые точки”, в малой окрестности которых нельзя добиться необходимой точности вычислений ни при какой самой мелкой разбивке (в этих точках теория упругости не применима). Такие же точки возникают в местах опирания труб на плоское основание. При определении давления грунта на жесткие круглые трубы, каковыми и являются в частности железобетонные трубы [1] эта трудность легко преодолевается следующим приемом: с помощью МКЭ определяется вертикальное и горизонтальное давление грунта во всех точках трубы, кроме особой; в особой точке прикладывается сосредоточенная сила, направленная вертикально в точке опирания труб или горизонтально в точке их со- прикасания, равная по величине площади эпюры соответственно вертикального и горизонтального давления грунта, действующего на трубы.
Собственный вес грунта насыпи распределяем согласно [2] по узлам разбивки следующим образом: в каждом узле данного треугольного конечного элемента прикладываем направленную вниз сосредоточенную силу, равную по величине весу части грунта, ограниченной этим элементом, деленной на число узлов. Поверхностная нагрузка распределяется по узлам верхней границы в виде сосредоточенных сил. Если же нужно получить матрицы влияния (функцию Грина), то необходимо провести расчеты на единичную сосредоточенную силу, прикладывая ее последовательно в каждом узле верхней границы. Моделирование материалов грунта, труб и других включений осуществляется с помощью соответствующих им значений упругих констант (Е,) и удельного веса. Это позволяет учитывать условия опирания труб, неоднородность и многослойность грунта насыпи и основания, многониточность укладки.
Вводимая информация содержит минимально необходимые данные высоты насыпи размеры труб, их количество и расстояние между ними: тип опирания труб; характеристики материала трубы и грунта насыпи: форма и положение поверхностной нагрузки.
Выводимая информация содержит величины вертикальных и горизонтальных перемещений узлов сетки, а также характеристики напряженного состояния внутри каждого элемента.
Для оценки достоверности полученных результатов было произведено тестирование программы МАС на задачах линейной теории упругости (плоская деформация), имеющих аналитическое решение:
а) растяжение пластинки с одним подкрепленным отверстием;
б) сжатие пластинки, с двумя подкрепленнымми круговыми отверстиями.
Расхождение результатов аналитических расчетов с результатами, полученными по МКЭ не превышает 3–5 %.
Кроме того, производилось сравнение с экспериментальными данными, полученными другими авторами для одиночной трубы. В этом случае расхождение составляет 15 %.
Далее, во втором параграфе, приведены численные результаты расчетов статического напряженно-деформированного состояния многониточных труб, находящихся в упругой среде.
Исследовано влияние количества ниток на напряженно деформированное состояние механических систем (рис. 1). Давление на крайние и средние трубы многониточной укладки (n
3) практически не зависит от количества ниток и для плотно уложенных труб составляет 15–20 %. Кроме того, с ростом коэффициента Пуассона грунта величина 
на крайнюю трубу снижается. При числе ниток n 4 величина 
на среднюю трубу практически не зависит от коэффициента 
. Результаты анализа максимального давления грунта на трубы двух и трех ниточной укладок в свету (d) между ними представлены на рис.1.
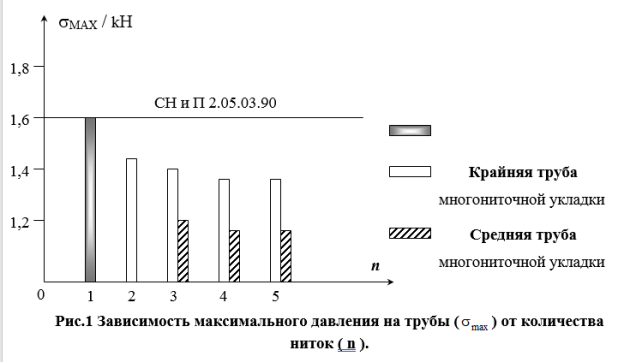
Рис. 1. Зависимость максимального давления на трубы () от количества ниток (n).
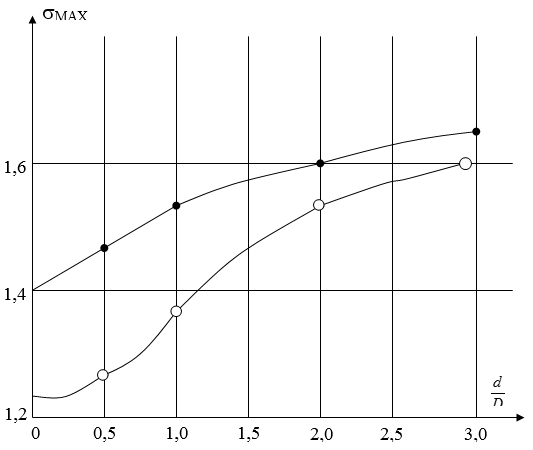
Рис. 2. Графики зависимости максимального давления грунта 
на трубы от расстояния в свету (d) между ним:
Графики на рис.2 показывают, что с увеличением расстояния между трубами величина возрастает. При 
увеличение 
незначительно (3 %), а при 
наблюдается существенный рост максимального давления грунта, затухающий при 
. При 
максимальное давление грунта на трубы, уложенные в несколько ниток, соответствует максимальному давлению на одиночно уложенную трубу и совпадает с величиной, определяемой по СНиП 2.05.03–90.
Таким образом, взаимное влияние труб многониточной укладки имеет место при расстоянии в свету между ними d<3D и приводит к снижению максимального давления грунта на них по сравнению с одиночно уложенной трубой.
Давление на среднюю и крайнюю трубу достигает минимального значения при d=0 труб, уложенных вплотную, и составляет соответственно 0,74 и 0,85 от максимального давления на одиночно уложенную трубу. На основе полученных зависимостей величины давления от расстояния между трубами выведены следующие формулы для определения коэффициентов давления грунта на трубы многониточной укладки при 
; 
,
при d/D>2.5
,
где 
коэффициенты, учитывающие снижение максимального давления грунта соответственно на крайнюю и среднюю трубу многониточной укладки по сравнению с одиночно уложенной трубой.
Также исследовано влияние расстояния между трубами на напряженно деформированное состояние механической системы.
Для более полного анализа давления грунта на трубы многониточной укладки рассмотрены эпюры радиальных 
и касательных (
) давлений грунта при различных параметрах укладки многониточных труб на плоское твердое основание.
Литература:
- И. И. Сафаров. Колебания и волны в диссипативно неоднородных средах и конструкциях. Ташкент: ФАН, 1992й., 250с.
- С. С. Каюмов, И. И. Сафаров. Распространение и дифракция волн в диссипативно-неоднородных цилиндрических деформируемых механических системах. Ташкент: ФАН, 2004й., 218с.
