В статье рассмотрены линейные колебания упругого полупространства при воздействии поверхностной волны Рэлея. Основной целью работы является исследование воздействия поверхностной волны Рэлея на цилиндрический слой. Определяется динамическое напряженное деформированное состояние цилиндрического слоя и окружающей его среды.
In this article there are considered the linear oscillations of the elastic half-space at effect of a surface wave of Rayleigh. The main purpose of this work is the research of effect of a surface wave of Rayleigh on cylindrical bed. There is determined the dynamic tight strained state of cylindrical bed and its environment.
Рассмотрим линейные колебания упругого полупространства при воздействии поверхностной волны Рэлея (Рис 1). Основной целью работы является исследование воздействия поверхностной волны Рэлея на цилиндрический слой. Определяется динамическое напряженное деформированное состояние цилиндрического слоя и окружающей его среды.
Предполагается, что связь между напряжением и деформацией полупространства и преграды удовлетворяет обобщенному закону Гука.
Математическая постановка задачи включает вариационное уравнение принципа возможных перемещений, по которому сумма работ всех активных сил, включая силы инерции, на возможном перемещении, удовлетворяющем геометрическим граничным условиям, равна нулю.
![]()
Здесь ![]() виртуальные работы внутренних напряжений, сил инерции и внешних сил, вычисляется по формулам
виртуальные работы внутренних напряжений, сил инерции и внешних сил, вычисляется по формулам
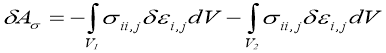
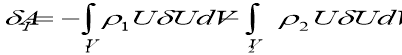
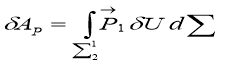
Ūj, ![]() ,
, ![]() — соответственно вектору перемещения компоненты тензоров напряжение и деформации; δ Ūj,
— соответственно вектору перемещения компоненты тензоров напряжение и деформации; δ Ūj, ![]() — вариации перемещения и деформации;
— вариации перемещения и деформации; ![]() ,
,![]() — плотность материала элементов рассматриваемой системы; ƒ — вектор массовых сил; ω — круговая частота; dV — элементное объем тело,
— плотность материала элементов рассматриваемой системы; ƒ — вектор массовых сил; ω — круговая частота; dV — элементное объем тело,
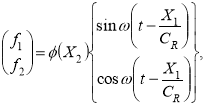
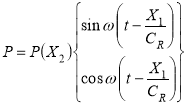
![]() (Х2) и Р(Х2) — известная функции координаты Х2.
(Х2) и Р(Х2) — известная функции координаты Х2.
До начала момента вращения ![]() точки рассматриваемой механической системы (рис. 1.) находятся в покое:
точки рассматриваемой механической системы (рис. 1.) находятся в покое:
![]() ;
; ![]() ;
;
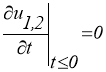
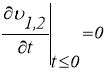
где — u1 и u2 перемещения частицы ![]() — по оси
— по оси ![]() ;
; ![]() и
и ![]() перемещения частицы —
перемещения частицы — ![]() по оси
по оси ![]() .
.
Внешние нагрузки, которые воздействует в цилиндрических преградах приняты как у плоской продольной упругой волны, которая задается в скоростях упругого смещения.
Предположим, что цилиндрический слой подкреплен в упругой среде. В этом случае должны выполняться условия непрерывности напряжений и перемещений на границе раздела ![]() :
:
Перемещение U точек рассматриваемой области находим в виде суммы:
![]() ,
,
где
![]()
![]()
![]()
![]() ,
,
Здесь U0 и V0- перемещения поверхностей полупространства при воздействии волны Рэлея; СR — скорости волны Рэлея. Задача решается методом конечных элементов [2].
При решении задач методом конечных элементов для не ограниченных областей необходимо из полуплоскости выделить (для исследования) расчетную область конечных размеров. Исследуемая область дискретизируется, причем возникает необходимость постановки таких условий на границе, которые бы не повлияли на результаты решения за счет отражения, что происходит при длительных динамических воздействиях.
В работе [1] были предложены граничные условия для конечной расчетной области, позволяющие моделировать бесконечную среду. Указанные граничные условия пропускают волну через границу расчетной области без отражения, т. е. получается так называемая стандартная вязкая граница (рис. 1). Задание стандартной вязкой границы осуществляется путем замены реакции не принимаемой во внимание части полуплоскости распределенными нагрузками σ и τ, вычисленными по формулам:
σ=α ρ CP![]() ; τ=βρСЅ
; τ=βρСЅ![]() ,
,
где ![]() и
и ![]() — скорости движения точек на границе тела соответственно по координатам Х1 и Х2; α и β — безразмерные параметры; ρ — плотность материала; CP и СЅ — скорости, соответственно продольных и поперечных волн.
— скорости движения точек на границе тела соответственно по координатам Х1 и Х2; α и β — безразмерные параметры; ρ — плотность материала; CP и СЅ — скорости, соответственно продольных и поперечных волн.
Дискретизация рассматриваемой области осуществляется с помощью треугольных элементов. Задача сводится к решению системы неоднородных алгебраических уравнений.
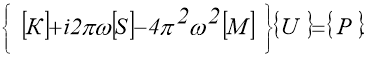
здесь {U} — вектор комплексных амплитуд колебаний системы; {Р}- вектор амплитуд внешней нагрузки; ω- частота внешней нагрузки. Система неоднородных комплексных алгебраических уравнений решалась методом Гаусса при следующих исходных данных:
ν1 = 0,20; ν2 = 0,33; Н/R=2,10; 15; Е1/Е2=0,1.
Результаты расчетов приведены на рис. 2. Произведен расчет на ЭВМ для 1020 треугольных конечных элементов. На рисунке 2 данные, представленные сплошной линией, получены в работе [3], а отмеченные звездочками получены по нашей методике при различных делениях расчетной области (1-N=45, 2-N=78, 3-N=144). Сравнение результатов, полученных по методы граничных элементов и методу конечных элементов, показывает, что максимальное различие между ними для кольцевых напряжений достигает 10–15 %.
Амплитуда перемещений на поверхности полупространства зависит от глубины залегания цилиндрической преграды. С ростом Н она экспоненциально затухает. Анализ этого решения позволяет сделать практический вывод. Протяженные подземные сооружения в сейсмически опасных районах являются как бы генераторами поверхностных волн при землетрясениях, преобразуя частично падающие сейсмические волны во вторичные поверхностные волны. Наличие на пути сейсмических волн такого рода неоднородностей влияет на формирование поверхностной волны Рэлея. Форма поперечного сечения цилиндрических тел не имеет принципиального значения для этого явления.
В области длинных волн глубина заложения особенно сильно влияет на напряженно — деформированное состояние. С увеличением глубины заложения (Н/α→∞) значения численных результатов стремятся к результатам решения задачи дифракции волн на теле, находящемся в безграничной среде.
![]()
![]()
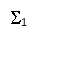
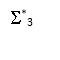
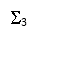
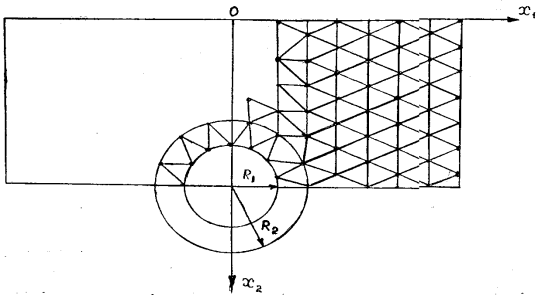
Рис. 1. Расчетная схема
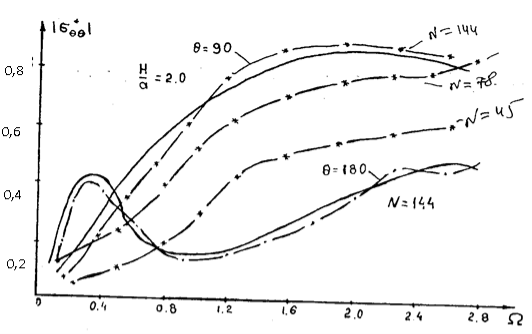
Рис. 2. Изменение кольцевого напряжения в зависимости от частоты внешних возмущений
Литература:
- Сафаров И. И. Мубораков Я. Н. Оценка сейсмонапряженного состояния подземных сооружений методом волновой динамики //сейсмодинамика зданий и сооружений. Ташкент: Фан,1988, с. 114–122.
- Сафров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях. Ташкент: Фан, 1992, с. 250.
- Митчелл Э., Уэйт Р., Метод конечных элементов для уравнений с частными производными. М., Мир, 1981, 329 с.

