В настоящее время при расчете различных железобетонных конструкций широкое развитие получает деформационная модель.
В современных нормах предложен подход к расчету прочности, жесткости и трещиностойкости железобетонных элементов с использованием нелинейной деформационной модели и диаграмм состояния бетона, т. е. зависимостей напряжения от деформации.
Учет в расчете железобетонных конструкций диаграмм деформирования, к которым применяются математические зависимости, позволяют учесть физические представления о работе бетона и арматуры, описать деформирование непрерывной кривой, получить хорошее совпадение опытных и расчетных данных и использовать полученные аналитические зависимости для составления алгоритмов при проектировании железобетонных конструкций с применением средств программирования.
На сегодняшний день, ввиду совершенствования теории железобетона, всесторонне исследуется нелинейная деформационная модель расчета, которая основана на использовании диаграмм деформирования бетона и арматуры. Эти диаграммы определяются за счет свойств материала, а также не зависят от геометрических размеров самой железобетонной конструкции.
На основе нелинейной деформационной модели предложен метод расчета железобетонного элемента, усиливаемого присоединением стальных элементов (уголков). Данный метод основан на первоначальных допущениях и предпосылках нелинейной деформационной модели при видоизменении выражений, которые являются определяющими для характеристик жесткости сечения, нормального к продольной оси элемента. Характеристиками жесткости учитываются такие показатели элементов усиливаемой железобетонной конструкции как площадь арматуры, ее положение в поперечном сечении, физико-механические свойства и бетона, и арматуры. Осуществление данного расчета рекомендуется проводить с использованием итерационного метода с учетом дальнейшего приближения окончательного результата вычислений. Плюс применения нелинейной деформационной модели состоит в том, что существует возможность применения новейших компьютерных технологий при ведении расчетов, а также непосредственное использование диаграмм деформирования бетона и стали арматуры без включения дополнительных упрощений и допущений.
Цель: разработка метода расчета железобетонной конструкции, которая усилена присоединением стальных элементов (уголков), на основе нелинейной деформационной модели.
Ключевые слова: усиление, присоединение стальных элементов (уголков), деформационная модель, железобетонный элемент, характеристики жесткости
Применение диаграммного метода расчета при проектировании и проведении научных исследованиях получает широкое распространение [2, 3]. Диаграммы деформирования материалов включены не только в нормативные документы на территории Российской Федерации, но и в странах ближнего и дальнего зарубежья.
В сводах правил по проектированию железобетонных конструкций указано следующее — расчет усиливаемых железобетонных конструкций необходимо производить по общим правилам расчета железобетонных конструкций. Данный момент является не противоречивым при использовании диаграммного метода расчета при усилении конструкций присоединением стальных элементов (уголков).
Основа принципа осуществления нелинейной модели — условное разделение расчетного сечения, нормального к продольной оси элемента, на элементарные участки малой площади. Распределение деформаций по элементарным участкам бетона и арматуры происходит по линейному закону, таким образом, справедлива гипотеза плоских сечений.
Величина внутренних усилий есть произведение матрицы жесткости элемента на значение общих деформаций (кривизны и относительной деформации продольной оси):
(1)
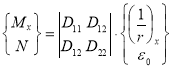(2)
где 
— это вектор-столбец внутренних усилий (изгибающего момента 
и продольной силы N); 
— вектор столбец общих деформаций (кривизны 
и относительной деформации продольной оси 
); 
— матрица жесткости сечения, нормального к продольной оси элемента.
Возможность видоизменения записи выражений для расчета компонентов матрицы жесткости 
(в общем случае i, j — 1, 2) предопределяет широкую применимость нелинейной деформационной модели на основе диаграмм деформирования материалов [4], в том числе к расчету железобетонных элементов, усиливаемых присоединением стальных элементов (уголков).
Изгибная жесткость плоскости изгиба:
(3)
Жесткость, которая обусловлена влиянием приращения момента на удлинение (или укорочение) продольной оси:
(4)
Жесткость, связанная с удлинением (или укорочением) элемента:
(5)
При расчете усиливаемых железобетонных элементов выражения характеристик жесткости
состоят из трех составляющих, которые учитывают бетон и арматуру усиливаемого элемента (по площадям участков бетона 
и стали арматуры 
), а также металл присоединенных стальных элементов (уголков) 
. Приведенные обозначения сохраняют единство с нормативными документами [1], индекс a несет информацию об усиливающей конструкции «каркас из стальных уголков» (рисунок 1).
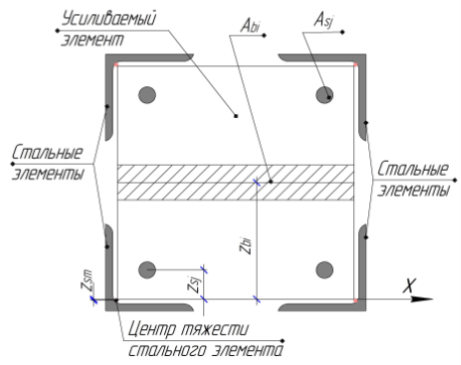
Рис. 1. Расчетная схема нормального сечения железобетонного элемента, усиленного присоединением стальных элементов (уголков)
Нумерация условных участков бетона ведется с индексом i, арматуры с индексом j, а усиливающего стального элемента m.
При осуществлении нелинейной деформационной модели, в уравнениях, записанных в форме матрицы, появляются две неизвестные: матрица жесткости 
и вектор-столбца общих деформаций
. Эти неизвестные функционально взаимосвязаны между собой.
Как было указано выше осуществление данного расчета, то есть расчета с применением деформационной модели, рекомендуется проводить с использованием итерационного метода с учетом дальнейшего приближения окончательного результата вычислений. Диаграммный метод выполняется путем постепенного итерационного уточнения коэффициентов упругопластических деформаций материалов по элементарным участкам разбиения, при этом контролируя результаты по величинам вектора-столбца общих деформаций элемента.
Вывод: рассмотренныйметод расчета усиления железобетонных конструкций путем присоединения стальных элементов (уголков) сохраняет все первоначальные плюсы деформационной модели, а именно учет нелинейных свойств материалов непосредственно через диаграммы деформирования бетона и арматуры, и определяются уровнем относительных деформаций; возможность автоматизирования процесса итерации окончательных результатов; оценка усиливаемой железобетонной конструкции по двум группам предельных состояний (по несущей способности и пригодности к эксплуатации).
Литература:
- СП 63.13330.2012. Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52–01–2003.
- Ерышев В. А., Тошин Д. С., Бондаренко А. С., Саратов Н. В., Тихонова Е. П. Диаграммный метод оценки деформаций изгибаемых железобетонных элементов при разгрузке // Вестник Волжского регионального отделения Российской академии архитектуры и строительных наук. — 2009. — № 12. — С. 182–188.
- Тошин Д. С., Анисимова М. П. Поиск оптимального способа реализации итерационного приближения при расчете по деформационной модели // Научное обозрение. — 2016. — № 17. — С. 25–29.
- Тошин Д. С. Прикладные возможности деформационной модели железобетона // Молодой ученый. — 2016. — № 29 (133). — С. 164–166.
