Приведен метод расчета железобетонного элемента, усиленного наращиванием (увеличением) сечения. Описываемый подход базируется на использовании нелинейной деформационной модели и гипотезе плоских сечений. В связи со сложившимися различиями напряженно-деформационного состояния усиленной и усиливающей частей, а также характеристик использованных материалов, элемент нельзя рассчитывать как единое целое. В алгоритм расчета вводятся прочностные и деформативные характеристики отдельно каждой части конструкции. Дальнейший расчет ведется итерационным способом с последовательными приближениями искомых величин. Данный метод позволяет рассчитать усиливаемый железобетонный элемент с учетом предыдущих нагружений и накопленных ранее деформаций, что в свою очередь дает более точную оценку работы конструкции после выполнения наращивания.
Ключевые слова: железобетон, нелинейная деформационная модель, наращивание сечения, железобетонный элемент, усиление, диаграммный метод
Традиционно усиленные конструкции рассчитываются методом предельных усилий так же, как и не усиленные. Однако в последние годы наблюдается тенденция перехода к расчету конструкций диаграммным методом, основанным на использовании диаграмм деформирования бетона и арматуры и реализуемом на основе деформационной модели. Этот метод давно и широко используется в зарубежных нормах [1]. В Российские нормативные документы [2] деформационный метод только начинает внедряться. Так в СП всесторонне не раскрыта тема, касающаяся расчета усиленных железобетонных элементов. Указывается лишь на то, что расчет в этих случаях производится по общим правилам проектирования железобетонных конструкций, но при условии обязательного учета напряженно-деформированное состояние конструкции до усиления. Однако метод расчета по предельным усилиям не дает оценку напряженно-деформированному состоянию конструкции до усиления, а также влияния начальных напряжений и деформаций на работу конструкции после ее усиления. А между тем, усиливаемая конструкция в процессе эксплуатации формирует некоторую историю нагружения, включая воздействия усилий различного происхождения и величины. Учитывая упругопластический характер деформирования материалов, в конструкции происходит накопление неупругих деформаций. Очевидно, что необходимы новые решения и методы расчета для усиливаемых конструкций, наиболее перспективные из которых базируются на использовании нелинейных диаграмм материалов и деформационной модели железобетона [3, 4].
Применение в расчетах диаграмм деформирования, выраженных математическими зависимостями «напряжение — деформация», позволяет учесть физические представления о работе конструкции. Связь между напряжением и деформациями описывается непрерывной кривой, которая используется при составлении алгоритмов и программ для автоматизации проектирования конструкций усиления.
Метод расчета по деформационной модели основывается на гипотезе плоских сечений, т. е. предположении линейного распределения деформаций бетона и арматура по высоте сечения.
В СП приведена запись выражения, характеризующего связь внутренних усилий с деформациями элемента:
{M}= [D]·{Ɛ}(1)
Либо следующим образом:
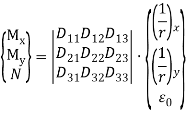 (2)
(2)
где {M} — столбец внутренних усилий; [D] — матрица жесткости сечения, нормального к продольной оси элемента; {Ɛ} — столбец общих деформаций.
В расчете для этого случая рассматриваются следующие физические зависимости:
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Жесткостные характеристики для этих выражений определяются при помощи численного интегрирования сечения, разделенного на ряд участков с координатами Zbx(y)i, Zsx(y)j и площадью Abi, Asj, соответственно:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (11)
(11)
Эти выражения справедливы для не усиленных элементов, на которые действует изгибающие моменты в двух взаимно перпендикулярных плоскостях, а также продольная сила от внешней нагрузки.
В случае расчета конструкций, усиливаемых наращиванием, к сечению добавляется дополнительный элемент, характеристики материалов которого могут отличаться от характеристик усиливаемого элемента. Кроме того к моменту наращивания усиливаемый элемент находится под нагрузкой, что определяет различия в напряженно-деформированном состоянии усиливаемой и усиливающей части сечения. Это приводит к тому, что элемент усиления нельзя рассчитывать как единый с основной усиливаемой конструкцией.
В предлагаемой методике предполагается, что гипотеза плоских сечений, принятая до усиления, справедлива для железобетонного элемента также после усиления. В математических записях жесткостных характеристик усиливаемый элемент учитывают отдельными слагаемыми, включающими характеристики и размеры наращивания:
![]() (12)
(12)
![]() (13)
(13)
![]()
![]() (14)
(14)
![]() (15)
(15)
![]()
![]() (16)
(16)
![]() (17)
(17)
Таким образом, последние два слагаемых, имеющие индекс ad относятся к усиливающей части конструкции — для бетона и арматуры. Индекс p характеризует порядковый номер элементарной площадки бетона, а индекс t — номер арматурного стержня в наращиваемой части элемента.
Реализация вычислительного алгоритма происходит с использованием итерационного метода расчета: искомые величины находятся путем последовательного приближения. При этом расчетное сечение разделяется на некоторое количество элементарных площадок [5], количество которых зависит от требуемой точности расчета, и возрастает при значительном градиенте деформаций.
Предложенный метод расчета усиливаемых элементов обладает рядом преимуществ: возможность автоматизации расчетов с использованием программных комплексов для удобства и простоты вычислений; единство сразу для двух групп предельных состояний; учет напряженно-деформированного состояния конструкции до усиления.
Литература:
- ENV 1992–1-1, Eurocode 2: Design of Concrete Structures. Part 1: General Rules and Rules for Building. — Brussels: European Committee for Standardization, 1992.
- СП 63.13330.2012 Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52–01–2003 (с Изменениями № 1, 2).
- Ерышев В. А., Тошин Д. С. Методика расчета нормального сечения изгибаемого железобетонного элемента при разгрузке // Известия высших учебных заведений. Строительство. — 2009. — № 6. — С. 97–104.
- Тошин Д. С. Прикладные возможности деформационной модели железобетона // Молодой ученый. — 2016. — № 29 (133). — С. 164–166.
- Тошин Д. С. О дискретизации нормального сечения железобетонного элемента с неоднородными свойствами бетона при расчете по нелинейной деформационной модели // Молодой ученый. — 2016. — № 27 (131). — С. 172–174.







