Целью научного исследования является формализация задач о построении оптимальных выпуклых тел в форме задач оптимального управления и нелинейного программирования, исследование свойств полученных задач, разработка, реализация и сравнение численных методов их решения.
Ключевые слова: опорная функция, поверхность вращения, радиус кривизны, нелинейное программирование, дискретная аппроксимация
Геометрические задачи о нахождении тел, максимальной или минимальной площади и объема с определенными ограничениями на ширину фигуры, широко распространены не только в математике, но и в практических приложениях. Такого рода задачи применяются в технике, производстве, задачах раскроя и упаковки, при размещении груза и объектов на различных транспортах. Знакомые задачи: Зедонора, в которой среди n-угольников, имеющих заданный периметр, требуется найти n-угольник максимальной площади; Архимеда, в которой необходимо найти шаровой сегмент, вмещающий наибольший объем среди всех сегментов, обладающей определенной площадью; Евклида и многие многие другие, решались еще в далеком прошлом. Поэтому решение экстремальных задач геометрии актуально и немаловажно не только с теоретической, но и с практической точки зрения. Формализовав задачуонахождения выпуклой, пространственной, центрально симметричной фигуры вращения максимальной площади поверхности при заданных ограничениях на ее ширину, как задачу математической теории оптимального управления. В работе при помощи программных средств рассматриваются и сравниваются результаты применения численных методов при построении «подозрительной на оптимальность» поверхности вращения.
Для описания свойств ограниченного замкнутого выпуклого множества используется его опорная функция, определяемая выражением:
![]() (1)
(1)
где ![]() — единичный вектор направления в сферической системе координат.
— единичный вектор направления в сферической системе координат.
С помощью опорной функции определяется ширина поверхности вращения: ![]() , диаметр: D=
, диаметр: D=![]() [2] и толщина множества:
[2] и толщина множества: ![]() Использование данного подхода позволяет формализовать ограничения на ширину рассматриваемых фигур, выразить такие характеристики, как периметр, площадь, объем, а также получить аналитическое выражение условий выпуклости. В частности, в случае плоской фигуры при введении полярной системы координат опорная функция является функцией полярного угла
Использование данного подхода позволяет формализовать ограничения на ширину рассматриваемых фигур, выразить такие характеристики, как периметр, площадь, объем, а также получить аналитическое выражение условий выпуклости. В частности, в случае плоской фигуры при введении полярной системы координат опорная функция является функцией полярного угла ![]() . При этом радиус кривизны фигуры в каждой точке вычисляется по формуле:
. При этом радиус кривизны фигуры в каждой точке вычисляется по формуле: ![]() , и в силу выпуклости фигуры, неотрицателен. Для вычисления периметра и площади могут быть использованы соотношения (2)-(3):
, и в силу выпуклости фигуры, неотрицателен. Для вычисления периметра и площади могут быть использованы соотношения (2)-(3):
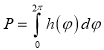 (2)
(2)
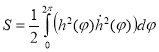 (3)
(3)
В работе приведенные соотношения служат основой для формализации рассматриваемых задач, решение которых сводится к определению опорной функции.
Задача о построении выпуклой фигуры ![]() , имеющей максимальную площадь поверхности S(F)
, имеющей максимальную площадь поверхности S(F)
Требуется найти выпуклую фигуру вращения максимальной площади поверхности:
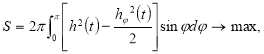 (4)
(4)
опорная функция![]() , которой удовлетворяет условиям:
, которой удовлетворяет условиям:
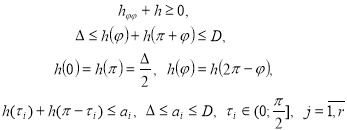 (5)
(5)
Введем функции ![]()
![]() , и обозначим независимую переменную через
, и обозначим независимую переменную через ![]() .
.
В новых обозначениях задача является задачей оптимального управления с фазовыми и промежуточными ограничениями
минимизировать функционал:
![]() (6)
(6)
при ограничениях:
![]() (7)
(7)
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,(8)
,(8)
![]() ,
, ![]() ,
,
![]()
![]() (9)
(9)
Дискретная аппроксимация
Разобьем равномерно отрезок интегрирования ![]() точками
точками ![]() ,
, ![]() , полагая
, полагая ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Обозначим
. Обозначим ![]()
![]()
![]() .
.
Используя формулы Эйлера аппроксимации производных: ![]() ,
, ![]() с учетом (7), получаем рекуррентные соотношения:
с учетом (7), получаем рекуррентные соотношения: ![]() При этом
При этом ![]() ,
, ![]() ,
, ![]() . Пусть
. Пусть ![]()
![]() — номера точек отрезка разбиения, соответствующих точкам
— номера точек отрезка разбиения, соответствующих точкам ![]() , отрезка
, отрезка ![]() . Дополнительные ограничения на ширину принимают вид:
. Дополнительные ограничения на ширину принимают вид: ![]()
![]() [5].
[5].
Метод левых прямоугольников
Расчёт интеграла в целевом функционале проводим по формуле левых прямоугольников. Дискретная задача, аппроксимирующая (6)-(9) с точностью ![]() , имеет вид:
, имеет вид:
минимизировать функцию
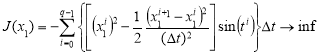 (10)
(10)
при ограничениях:
![]() (11)
(11)
![]()
![]()
![]() ,(12)
,(12)
![]()
![]() .(13)
.(13)
При такой постановке задачи становится доступным широкий спектр методов математического программирования с высокой скоростью сходимости. В частности, для решения рассматриваемой задачи применен метод градиентного спуска. Ограничения на переменные учитываются с помощью проекции градиента. Для определения направления приближения к экстремуму применяется наискорейший спуск.
В методе наискорейшего спуска шаг градиентного спуска ![]() выбираем из условий:
выбираем из условий: ![]() ,
, ![]() . На каждой итерации данная одномерная задача оптимизации решается методом дихотомии с заданным интервалом изменения
. На каждой итерации данная одномерная задача оптимизации решается методом дихотомии с заданным интервалом изменения ![]() , равным
, равным ![]() , и точностью определения решения
, и точностью определения решения ![]() . Градиент минимизируемой функции вычисляем по формулам [5]:
. Градиент минимизируемой функции вычисляем по формулам [5]:
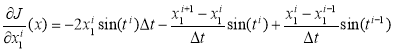
![]() (14)
(14)
Метод Симпсона
Для вычисления интеграла в целевом функционале можем использовать формулу Симпсона. Дискретная задача, аппроксимирующая исходную задачу с использованием схемы Симпсона, имеет вид: минимизировать функционал
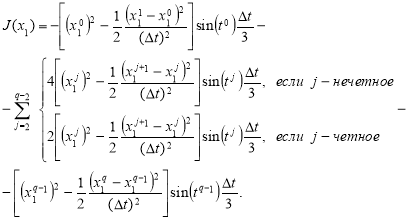 (15)
(15)
при ограничениях:
![]()
(16)
![]()
![]()
![]() ,(17)
,(17)
![]()
![]() .(18)
.(18)
Градиент минимизируемой функции вычисляем по формулам:
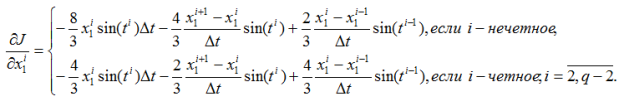 (19)
(19)
Сравнительный анализ интегральных методов
Приведем результаты решения задачи в таблице 1 методом градиентного спуска с помощью формул левых прямоугольников и формулы Симпсона рис.1 и 2. Построено оптимальное решение задачи при наборах параметров: 1) q=500, ![]() =0,9,D=1,
=0,9,D=1, ![]() =
=![]() =
=![]() и 2) q=2000,
и 2) q=2000, ![]() =0,9,D=1,
=0,9,D=1, ![]() =
=![]() =
=![]() .
.
Таблица 1
Сравнительный анализ интегральных методов
|
Параметры: q=500
|
Методы |
Параметры: q=2000
|
Методы | |||
|
Левых прямоуго-льников |
Симпсона |
Левых прямоуго-льников |
Симпсона | |||
|
Количество итерации |
27357 |
256 |
Количество итерации |
22098 |
213 | |
|
Время расчетов, мин |
22 |
2 |
Время расчетов, мин |
20 |
1 | |
|
Достигнутая точность |
|
|
Достигнутая точность |
|
| |
|
Значение минимизируе-мой функции |
-3,1229 |
-3,1169 |
Значение минимизируе-мой функции |
-3,1265 |
-3,1158 | |
Построено численное решение (15)-(18) при следующих значениях параметров: q=500, ![]() =0,9,
=0,9,![]() =
=![]() =
=![]() . На рис.1. приведены графики функций
. На рис.1. приведены графики функций ![]() , и сечение фигуры полученных методом проекции градиента.
, и сечение фигуры полученных методом проекции градиента.
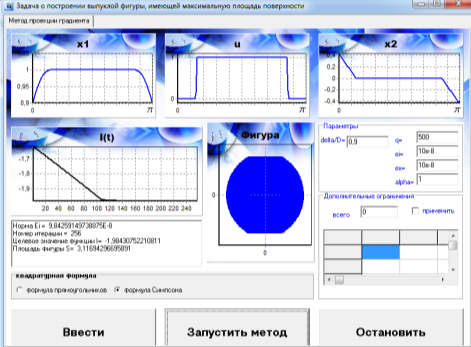
Рис. 1. Экранная форма интегральных методов без ограничений на ширину
Приведем результаты решения задачи (15)-(18) методом проекции градиента с одним активным дополнительным ограничением. Построено оптимальное решение задачи при значениях параметров: q=500, ![]() =0,9,D=1,
=0,9,D=1, ![]() =
=![]() =
=![]() . На рис.2 представлена экранная форма программного продукта, построены графики
. На рис.2 представлена экранная форма программного продукта, построены графики ![]() и сечение фигуры, соответствующих оптимальным решениям задачи.
и сечение фигуры, соответствующих оптимальным решениям задачи.
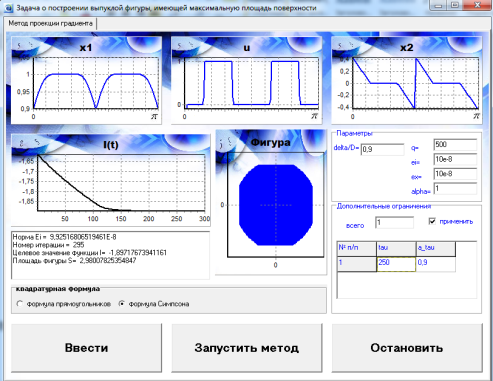
Рис. 2. Экранная форма интегральных методов при одном дополнительном ограничении
Сравнительный анализ градиентных методов
Для определения направления приближения к экстремуму в методе градиентного спуска применим метод Ньютона. Гессиан минимизируемой функции вычисляем по формулам [2], [5]:
![]() ,
, ![]()
![]() ,
,![]()
![]() ,
, ![]() (20)
(20)
Приведём сравнительный анализ численных решений рассматриваемой задачи, полученных методом градиентного спуска, наискорейшего спуска, сопряженных градиентов, Ньютона, Флетчера-Ривза. Результаты численных экспериментов и анализ эффективности методов при решении задачи для 500 и 2000 точек разбиения приведены, соответственно, в табл. 2 и 3. Метод Ньютона сходится быстрее и позволяет получить более точное решение, если начальная точка, из которой запускается численный процесс оптимизации, находится в некоторой окрестности одной из точек минимума. В качестве такой точки целесообразно выбирать решение, полученное методом наискорейшего спуска.
Таблица 2
Сравнительный анализ градиентных методов
|
Параметры: q=500
|
Методы | ||||
|
Градиентного спуска |
Наискорей-шего спуска |
Флетчера-Ривза |
Сопряжен-ных градиентов |
Ньютона | |
|
Количество итерации |
27357 |
16458 |
1745 |
18 |
10 |
|
Время расчетов, мин |
22 |
12 |
8 |
0,08 |
0,009 |
|
Достигнутая точность |
|
|
|
|
|
|
Значение минимизируемой функции |
-3,1229 |
-3,1238 |
-3,1241 |
-3,1245 |
-3,1239 |
Таблица 3
Сравнительный анализ градиентных методов
|
Параметры: q=2000
|
Методы | ||||
|
Градиентного спуска |
Наискорей-шего спуска |
Флетчера- Ривза |
Сопряжен- ных градиентов |
Ньютона | |
|
Количество итерации |
22098 |
57814 |
1689 |
17 |
11 |
|
Время расчетов, мин |
20 |
23 |
7 |
0,09 |
0,008 |
|
Достигнутая точность |
|
|
|
|
|
|
Значение минимизируемой функции |
-3,1265 |
-3,1263 |
-3,1264 |
-3,1265 |
-3,1265 |
Результаты, полученные в работе численно, соответствуют аналитическому решению данной задачи, приведенные во многих работах Андреевой Е. А. [2], Цветковой Е. Г. [5], Красноженова Г. Г. [4] и других.
Литература:
- Andreeva E. A., Klötzler R. Zur analytischen Lösung geometrischer Optimierungsaufgaben mittels Dualität bei Steuerungstheorie // ZAMM. 1984.
- Андреева Е. А., Цирулева В. М. Численные методы решения экстремальных задач. Тверь, 2002.
- Евтушенко Ю. Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.:Наука, 1982.
- Красноженов Г. Г. Применение численных методов к решению экстремальных задач геометрии. Диссертация канд. ф.м. наук. Тверь, ТвГУ, 2001.
- Цветкова Е. Г. Решение экстремальных задач геометрии методами оптимального управления и нелинейного программирования // Математика. Информационные технологии. Образование: Сборник научных трудов. Оренбург: ОГУ, 2008. С.103–106.
- Цветкова Е. Г. Применение методов нелинейного программирования к решению экстремальных геометрических задач// Математические методы управления: Сборник научных трудов. Тверь: ТвГУ, 2009. С. 97–108.

