Пусть –трехмерный тор. Рассмотрим функцию вида

,

где –вещественнозначная условно отрицательно определенная функция на и следовательно, является четным и имеет единственный минимум в точке .

Отметим, что комплекснозначная ограниченная функция называется условно отрицательно определенным, если и

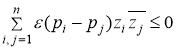
для любых и , а также для любого удовлетворяющего условию .

Положим

,

,

и

.

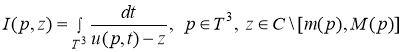Основным результатом настоящей работы является следующая теорема.

Теорема 1. Функция имеет максимум в точке такое, что для некоторого имеет место нижняя оценка

.

Доказательство. Сначала напомним, что вещественнозначная четная условно отрицательно определенная функция представляется в виде [1]

,

которое эквивалентно тому, что коэффициенты Фурье с условием являются неотрицательными, т. е.

и ряд сходится абсолютно.

Так как является четной функцией, также является четной. Следовательно, из равенства

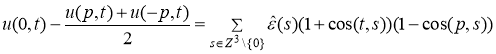
следует, что

,

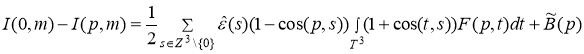где

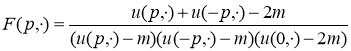
и

.

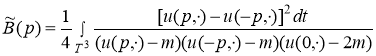Положим

.

Запишем функцию как сумма двух функций

и

.

Пусть –характеристическая функция множества . Положим . Тогда для любых и функция строго положительно. Так как функция имеет единственный минимум в точке , функция принадлежит Банахово пространство . Тогда для некоторого (достаточно большого) , достаточно малого и для всех имеет место неравенство

.

Из леммы Римана-Лебега следует, что

при .

Из непрерывности функции

в компактном множестве следует, что для всех и верна .

Положим . Тогда при всех имеет место . Таким образом, из , следует, что , . Следовательно,

.

Отсюда и следует доказательство теоремы 1.

Литература:

1. C.Berg, J. P. R. Christensen and P. Ressel. Harmonic analysis on semigroups. Theory of positive definite and related functions. Graduate Texts in Mathematics. Springer-Verlag, New York, 1984, 289 pp.