Введение
Задача портфельной оптимизации состоит в том, чтобы выбрать из совокупности различных портфелей тот, который по результатам наблюдений принесёт инвестору в течение некоторого периода наилучший результат. Два основных параметра, по которым инвестор принимает окончательное решение о вложении капитала – это риск и доходность. Сравнивая и оценивая эти показатели, потенциальный инвестор делает вывод о привлекательности объекта. Многие исследователи формируют интегральные показатели, которые учитывают оба фактора и называют их также мерами риска. Исторически первой такой функцией является функция Марковица [1]:
|
D[U]-aE[U], |
(1) |
где U - случайная величина - будущая доходность портфеля, D и E - соответстенно дисперсия и математическое ожидание. Положительный параметр a характеризует склонность инвестора к риску: чем больше a, тем более инвестор склонен к риску.
В рамках данной работы предлагается использовать комплексный показатель, сочетающий в себе квантильные меры риска (VaR-CVaR) [3] и асимметрию распределения доходности. Квантильные меры риска и асимметрия основаны на принципиально разных подходах к пониманию и оценке риска. Квантильные меры рассматривают риск как минимальную границу доходности с некоторым уровнем достоверности, асимметрия - это мера отклонения распределения от симметричности. Совмещение этих двух подходов позволит учесть различные характеристики распределения доходности.
Портфель ценных бумаг
Пусть рассматриваются n видов ценных бумаг. Под портфелем будем понимать вектор 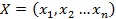 , где
, где 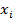 - доля i-ой акции в портфеле, т.е.
- доля i-ой акции в портфеле, т.е. 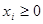 ,
, 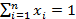
Пусть 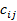 – цена (курс, котировка)
– цена (курс, котировка) 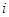 -й акции в
-й акции в 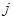 -й день
-й день 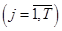
Наблюдения над ценами акций образуют матрицу:
|
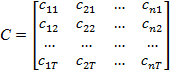
размеров
|
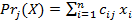
Для сопоставимости доходности различных инструментов для каждой ценной бумаги определяется отношение стоимости ценной бумаги в момент времени 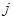 (
(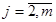 ) к стоимости этой бумаги в начальный момент времени
) к стоимости этой бумаги в начальный момент времени 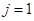 .
.
|
|
|
(2) |
Здесь величина в знаменателе равна начальной стоимости портфеля.
Пусть рассматривается некоторое семейство мер риска Yr(X), зависящих от портфеля X и векторного параметра r. Например, у меры Марковица (1) параметр r одномерный (коэффициент склонности к риску a). При выборе меры риска, которую следует использовать инвестору с учетом его индивидуальных предпочтений, модель необходимо калибровать, т.е. подобрать параметр r, обеспечивающий формирование оптимального портфеля. Методика калибровки модели описана в [4].
Методика калибровки модели
Пусть по наблюдениям за курсами акций на временном промежутке длительностью T инвестор желает сформировать портфель на последующий короткий временной промежуток t, причем эффективность портфеля X инвестор оценивает значением некоторой функции jt(X). Для этого целесообразно по историческим данным проанализировать эффективность портфелей, минимизирующих меру риска Yr,T(X) при различных значениях параметра r из некоторой области R и попытаться выбрать значения, при которых получена максимальная эффективность полученного портфеля. Тем самым, необходимо решить следующую двухэтапную оптимизационную задачу:
|
|
(3) |
|
|
(4) |
Здесь 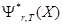 - статистическая оценка меры риска, вычисленная по историческим данным на временном промежутке T.
- статистическая оценка меры риска, вычисленная по историческим данным на временном промежутке T.
Если удается в результате решения оптимизационной задачи (3) - (4) при сдвиге исторических временных интервалов T, t выделить множество
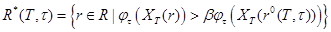 ,
,
где число b достаточно близко к 1 (0,95; 0,99), то значения параметров из множества 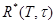 можно рекомендовать к использованию при формировании оптимального портфеля.
можно рекомендовать к использованию при формировании оптимального портфеля.
Меры риска
В работе рассматриваются индексные меры риска, основанные на мерах VaR и CVaR.
|
|
(5) |
|
|
(6) |
Здесь X – портфель, V(X) – случайная величина – доходность портфеля X, P – вероятность, a - достаточно малое положительное число (0,1; 0,05; 0,01), E – математическое ожидание, распределение доходности предполагается непрерывным. VaR является 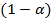 - квантилем распределения доходности. Поскольку наряду с левыми рассматриваются и правые хвосты, то величины, определенные равенствами (5) и (6) далее будут обозначаться
- квантилем распределения доходности. Поскольку наряду с левыми рассматриваются и правые хвосты, то величины, определенные равенствами (5) и (6) далее будут обозначаться 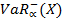 и
и 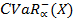 . Тогда аналогичные характеристики для правого хвоста распределения доходности:
. Тогда аналогичные характеристики для правого хвоста распределения доходности:
|
|
(7) |
|
|
(8) |
Наряду с этими величинами в рассматриваемые меры риска включается коэффициент асимметрии 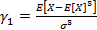 , где s - стандартное отклонение.
, где s - стандартное отклонение.
Исследуются две новые меры риска:
- линейная комбинация индексной меры VaR и коэффициента асимметрии:
|
|
(9) |
- линейная комбинация индексной меры CVaR и коэффициента асимметрии:
|
|
(10) |
Отношения квантильных мер риска аналогично индексу Рачева [5], идея использования коэффициента асимметрии в качестве показателя риска сформулирована там же.
Коэффициент α позволяет изменять длину «хвостов». Чем больше α, тем длиннее «хвосты» и тем ближе VaR к среднему значению случайной величины X. Если α слишком мало, то «хвосты» не дают адекватной оценки поведения X. В то же время, если α велико, то полученные значения малоинформативные. Как можно убедиться, инвестору выгодно уменьшать первое слагаемое в выражениях (9) и (10).
Экономический смысл коэффициента асимметрии заключается в следующем: если он имеет положительное значение (положительный скос), то более высокие доходы (правый “хвост”) являются более вероятными, чем низкие и наоборот. Понятно, что чем он больше, тем лучше выбран портфель. Положительный коэффициент β позволяет изменять влияние 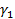 при вычислении комплексной меры риска. Из приведенных соображений, как и было сформулировано ранее, меры (9) и (10) целесообразно уменьшать.
при вычислении комплексной меры риска. Из приведенных соображений, как и было сформулировано ранее, меры (9) и (10) целесообразно уменьшать.
Наряду с указанными для сравнительного анализа применялся индекс Шарпа с нулевой безрисковой ставкой [2]:
|
|
(11) |
По сравнению со стандартным подходом в (11) добавлен знак «-» для того, чтобы в соответствии с предыдущим выражением меру риска надо было минимизировать.
Меры риска M1, M2, M3 для дальнейшего описаны аналитически.
Пусть P1(X)£P2(X)£…£PT(X) - упорядоченная по возрастанию последовательность доходностей портфеля X за T дней наблюдения, l=α T. Тогда
|
|
(12) |
|
|
(13) |
Из представлений (12), (13) с использованием стандартных выражений для статистических оценок получается:
|
|
(14) |
|
|
(15) |
Поскольку значение T предполагается достаточно большим, для упрощения записи при вычислении стандартного отклонения используется знаменатель T вместо T-1.
Мера M3 вычисляется аналогично. Доходности Pi(X) выражаются через компоненты вектора X по формуле (2).
|
Алгоритм решение задачи (3) при фиксированных параметрах (α и β) в мерах риска M1 и M2 описан ниже.
1. Генерируется случайная точка, случайно распределенная в симплексе xi³0, 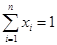
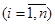 в соответствии с нормальным законом распределения.
в соответствии с нормальным законом распределения.
2. Далее применяется градиентный метод в форме Франка-Вульфа [7], в качестве начального принимается портфель X(0)= (x1,…,xn), сгенерированный на первом этапе.
Приближение X(k+1) строится следующим образом. На симплексе
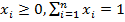 минимизируется линейная функция
минимизируется линейная функция 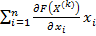 , где в качестве функции F принимается та или иная мера риска (9)-(11). Пусть решение этой задачи Y(k). Принимается X(k+1)= X(k)+l(Y(k)-X(k)), где l - шаг вычислений. Если точка оказывается вне симплекса, то уменьшается шаг так, чтобы точка X(k+1) оказалась на границе симплекса.
, где в качестве функции F принимается та или иная мера риска (9)-(11). Пусть решение этой задачи Y(k). Принимается X(k+1)= X(k)+l(Y(k)-X(k)), где l - шаг вычислений. Если точка оказывается вне симплекса, то уменьшается шаг так, чтобы точка X(k+1) оказалась на границе симплекса.
Построение продолжается, пока не получим нулевого градиента, точку на границе или не будет достигнуто неравенство, 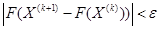 , где e - принятая точность вычислений.
, где e - принятая точность вычислений.
3. Шаги 1 и 2 повторяются, пока не будет достигнута стабилизация рекордного значения функции F. В частности, критерием стабилизации является неулучшаемость рекордного значения при 10 повторениях шагов 1-2.
Результаты вычислительного эксперимента
Вычислительная схема реализована в среде Delphi. Информационную базу данных составили архивы котировок акций, размещенные на сайтах Российской торговой системы [7] и РИА «РосБизнесКонсалтинг» [8]. Для анализа были взяты котировки по 19 акциям и 1 облигации за период с 01.08.2006 по 31.07.2009 (около 3 лет). Период T (см. (3) составил 27 месяцев - 1094 торговых сессии. В качестве функции j принимались доходность, промежуток t принимался равным одному месяцу (июль 2009 года), одной неделе (последняя неделя июля 2009 года), одному дню (31 июля 2009 года).
Для мер M1, M2 задача (4) решалась на сетке: параметр α изменялся в интервале [0,01;0,4] с шагом 0,01; а параметр β в интервале [1;5] с шагом 1.
Оказалось, что для всех трех временных промежутков значения параметров α, β, при которых получен оптимальный портфель, очень близки. Результаты численного эксперимента приведены в таблице 1.
Таблица 1.
|
Мера риска |
Сравнение с индексом Шарпа и характеристики портфелей при различных комбинациях α, β |
Оптимальные значения параметров |
|
|
1. При α>0,3 доходность ниже, чем при использовании индекса Шарпа при любом 2. При увеличении коэффициента |
α: от 0,15 до 0,25 β: от 1 до 3 |
|
|
1. При любом 2. Доходность при увеличении |
α: от 0,2 до 0,3 β=2, β=4. |
Заключение
В работе предложены новые индексные меры финансового риска, исследована эффективность их применения при формировании портфелей, произведена калибровка соответствующих портфелей.
Результаты анализа вычислительного эксперимента показали следующее.
1. Использование индексной меры, основанной на CVaR и асимметрии, приводит к формированию более эффективного портфеля, нежели при использовании индекса Шарпа и меры, основанной на VaR.
2. Уровень диверсифицированности оптимальных портфелей, построенных на базе предложенных мер, весьма высок. Диверсифицированность высока как по видам ценных бумаг, так и по отраслям.
Литература
1. Markowitz H.M. Portfolio Selection The Journal of Finance. 1952, v.7 (1): 77–91.
2. Sharpe W.F. Mutual Fund Performance Journal of Business (January), 1966, p. 119-138.
3. Uryasev S: VaR vs CVaR in Risk Management and Optimization. Tutorial. 2008.
5. Rachev S.T., Menn C., Fabozzi F.J. Fat-Tailed and Skewed Asset Return Distribution. // Wiley Finance, 2005
6. Акулич И.Л. Математическое программирование в примерах и задачах. // Высшая школа, 1986
7. www.rts.ru
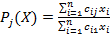 .
.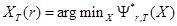 ,
,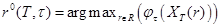 .
.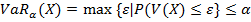 ,
,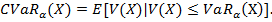
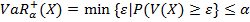 ,
,
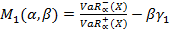 ,
,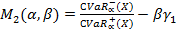 .
.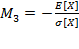 .
.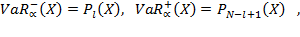
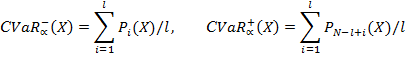
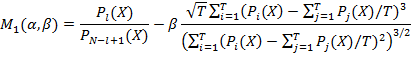
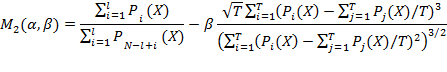
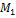
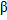 .
.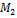
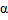 доходность выше, чем при использовании индекса Шарпа.
доходность выше, чем при использовании индекса Шарпа.
