Работа выполнена при поддержке гранта № МК-5098.2016.8
Аэродинамическим экспериментом называют моделирование течений воздуха и их взаимодействие с исследуемыми объектами с целью изучения. При решении задач аэродинамики теоретические методы не всегда позволяют получить достоверные результаты, поскольку математические модели явлений несовершенны. Поэтому наряду с законами подобия используется аэродинамический эксперимент для наиболее надежного определения аэродинамических характеристик среды и исследуемого объекта. В данной статье рассмотрены методы аэродинамического эксперимента.
Ключевые слова: аэродинамический эксперимент, аэродинамическая труба, ракетная тележка, баллистическая установка, ротативная машина.
Аэродинамический эксперимент можно разделить на две группы в зависимости от относительного движения воздушной среды и исследуемого объекта:
1) исследуемый объект движется с определенной скоростью в неподвижной воздушной среде;
2) неподвижный исследуемый объект в воздушной среде, движущейся с определенной скоростью.
К первой группе относятся такие эксперименты как летные испытания, баллистическая установка, ротативная машина и ракетная тележка. Ко второй же относятся аэродинамические трубы.
Баллистическая установка
Для исследования взаимодействия свободнолетящего тела с обтекающим его газом используется баллистическая установка. Целью таких исследований является изучение аэродинамического сопротивления и устойчивости движения тела, звукового удара и т.д.
Состоит баллистическая установка из метательного устройства, сообщающего скорость исследуемому телу, баллистической трассы вдоль траектории полёта тела, оборудованной измерительной аппаратурой, и устройства для торможения тела. В качестве метательного устройства используется пороховая пушка или двухступенчатая пушка, называемая легкогазовой (см. рис.1). Она представляет собой два ствола, в первом пороховой заряд движет поршень, сжимающий легкий газ во втором стволе до больших давлений. Когда давление достигает заданного экспериментом значения, срабатывает спусковое устройство и модель приводится в движение. Скорость метания таких пушек достигает 11 км/ч.
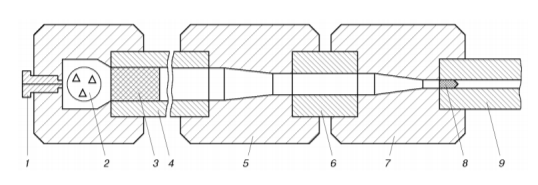
Рис. 1. Схема легкогазовой установки с составным коническим переходником:
1 — запальная пробка, 2 — пороховая камера, 3 — поршень, 4 — камера сжатия, 5 — первая секция конического переходника, 6 — цилиндрическая вставка, 7 — вторая секция конического переходника, 8 — метаемый элемент, 9 — ствол
Ротативная машина
Ротативную машину применяют в экспериментах, где исследуемому телу придают вращательное движение относительно неподвижной среды. Основным элементом ротативной машины является брус, который вращается вокруг оси, не совпадающей с главной осью самого рычага. С одного конца бруса устанавливается исследуемый объект, с другой стороны устанавливается противовес для уравновешивания массы и момента инерции исследуемого тела. Иногда около исследуемого тела устанавливается круговой экран с прорезью для прохождения бруса, который позволяет убрать влияние на исследуемый объект спутной струи, которая вызывается вращающимися частями установки.
Ракетная тележка
Совершенствование методов испытаний новых образцов ракетной и оборонной техники привело к созданию специальных высокоскоростных железных дорог, которые были названы ракетными треками. Первые сведения об испытания при помощи ракетных тележек были опубликованы в 1957 году в журнале Jet Propulsion. Ракетные треки представляют собой закрепленные на двух, связанных фундаментом, жестких балках направляющие с ширеной колеи 1-2 м и протяженностью до 11 км. Близкие к натуральным условия движения испытуемых образцов на дозвуковой и сверхзвуковой скоростях, воспроизводятся с помощью специальных тележек, которые движутся по ракетным трекам под действие реактивной тяги пороховых реактивных двигателей. Ракетные тележки имеют скользящие опоры, называемые башмаками, которые огибают головку рельса своими нижними захватами. Это позволяет воспринимать момент сил относительно центра масс движущейся системы. Широкое распространение на ракетных треках получили испытания головных частей ракет, парашютных систем, взрывательных устройств, стекол кабин самолетов на птицестойкость и т.п. [1].
Летные испытания
Летные испытания широко применяются при создании и сертификации самолета и включают исследования на стендах, летающих лабораториях и сертифицируемом самолете [2]. Но хоть летные испытания дают наиболее достоверные зависимости между изучаемыми параметрами, такие испытания очень сложны и требуют больших затрат труда, средств и времени. Если бы исследования начинались с натурных условий, летный эксперимент мог бы привести к непоправимым последствиям. Исходя из данных соображений, опыты в натуральных условиях обычно проводятся на заключительном этапе во всем ряде расчетно-теоретических работ, экспериментов на моделях, часто дополняют и завершают эксперимент в аэродинамических трубах.
Аэродинамические трубы
Аэродинамические трубы являются основными в исследовании различных параметров на моделях и отдельных элементах летательного аппарата. Чтобы перейти от лабораторной модели к настоящему летательному аппарату нужно выдержать равенство некоторых безразмерных параметров. Эти безразмерные параметры называют критериями подобия. Аэродинамические трубы позволяют создать такой поток воздуха, который отвечает определенному критерию подобия. Аэродинамическая труба представляет собой замкнутый воздушный канал (см. рис. 2); в рабочей части трубы 1 на аэродинамических весах 2 установлена испытываемая модель 3. По замкнутому воздушному каналу вентилятор 6, который приводится в движение электромотором 7, прогоняет воздух. Пройдя через спрямляющую решетку 9, служащую для создания равномерного поля скоростей по всему сечению трубы, и сужающуюся часть трубы (конфузор) 10, где воздух разгоняется до необходимой скорости, воздушный поток входит в рабочую часть трубы. После прохождения воздушного потока через рабочую часть трубы, он попадает в расширяющуюся часть трубы (диффузор) 4, где плавно тормозится, что снижает сопротивление движению воздуха по каналу и в поворотных лопатках и увеличивает КПД вентилятора. Лопасти вентилятора защищены прочной сеткой 5 от повреждений на случай возможного разрушения испытываемой модели. Система поворотных лопаток 8 обеспечивает плавное течение воздушного потока по каналу трубы.
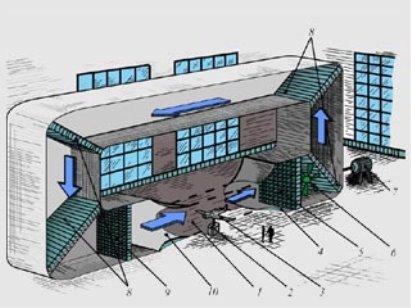
Рис. 2. Принципиальная схема аэродинамической трубы
Аэродинамические трубы классифицируют по диапазону возможных скоростей потока (дозвуковые, трансзвуковые, сверхзвуковые, гиперзвуковые), размеру и типу рабочей части (открытая, закрытая), а также поджатию — соотношению площадей поперечных сечений сопла трубы и форкамеры. Также существуют отдельные группы аэродинамических труб:
- Высокотемпературные— дополнительно позволяют изучать влияние больших температур и связанных с ними явлений диссоциации и ионизации газов.
- Высотные— для исследования обтекания моделей разреженным газом (имитация полёта на большой высоте).
- Аэроакустические— для исследования влияния акустических полей на прочность конструкции, работу приборов и т.п.
Дозвуковая аэродинамическая труба постоянного действия состоит из рабочей части, в виде цилиндра с поперечным сечением в форме круга или прямоугольника (иногда эллипса или многоугольника). Рабочая часть может быть, как закрытой, так и открытой. При этом если необходимо создать аэродинамическую трубу с открытой рабочей частью, статическое давление в которой не равно атмосферному, струю в рабочей части отделяют от атмосферы высотной камерой или камерой Эйфеля. Существенной особенностью дозвуковых аэродинамических труб является возможность изменения скорости газа в рабочей части за счёт изменения перепада давления.
В общих чертах схемы сверхзвуковой и дозвуковой аэродинамических труб аналогичны. Для получения сверхзвуковой скорости газа в рабочей части применяют сопло Лаваля, которое представляет собой сначала сужающийся, а затем расширяющийся канал. В сужающейся части скорость потока увеличивается и в наиболее узкой части сопла достигает скорости звука. В расширяющейся части сопла скорость становится сверхзвуковой и увеличивается до заданного значения, соответствующего числу махав рабочей части. Каждому числу маха отвечает определённый контур сопла. Поэтому в сверхзвуковых аэродинамических трубах для изменения числа маха в рабочей части применяют сменные сопла или сопла с подвижным контуром, позволяющим менять форму сопла.
Высокоэнтальпийные установки кратковременного режима (см. рис. 3) позволяют воспроизводить натуральные давления и температуры в широком диапазоне сверх- и гиперзвуковых скоростей и высот полета летательных аппаратов. Такие установки называются импульсными аэродинамическими трубами [3]. Рабочий газ заключен в канал с внутренним диаметром 70 мм и длиной 6 м. Электрический подогреватель, охватывающий канал снаружи, нагревает газ до заданной температуры. В конце канала последовательно размещаются диафрагмы, профилированное сопло, рабочая часть диаметром 0.5 м и выхлопная система. Имеются профилированные сопла, рассчитанные на числа Маха М = 5, 6, 8 и 10. После разрыва диафрагмы происходит стационарное истечение газа из канала в рабочую часть. Его продолжительность (до 40 мс) определяется временем пробега волны разрежения от сопла до противоположного конца канала и обратно до сопла [4].
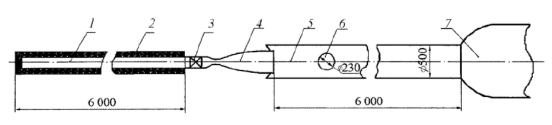
Рис. 3. Схема ударной аэродинамической трубы УТ-1М в виде трубы Людвига:
1 — тепловая камера; 2— электрический подогреватель; 3 — диафрагменный отсек; 4 — сверхзвуковое сопло; 5 — рабочая часть; 6 — оптическое окно; 7 — вакуумная емкость
Литература:
- Балакин В. А. Высокоскоростное трение на ракетном треке // Трение и износ. – 2005. – Т. 26. –№ 3. – С. 255-260.
- Ахметшин. Т. Ф. Сертификация авиационной техники //Вестник УГАТУ. – 2013, с 10-18.
- Маслов А. А., Шумский В. В., Ярославцев М. И. Импульсная аэродинамическая труба с комбинированным нагревом и стабилизацией параметров //Прикладная механика и техническая физика. – 2012. – С 3-10.
- Боровой В. Я., Бражко В. Н., Егоров И. В., Зайцев Е. Г., Скуратов А. С. Диагностика и численное моделирование течения в гиперзвуковых аэродинамических трубах импульсного действия // Ученые записки ЦАГИ. – 2013. – С. 28-38.
- Сафронов А. И., Зоркин В. А., Потапенко В. В. Анализ и баллистическое проектирование лабораторной установки малого калибра с присоединенными камерами подгона // Вестник Самарского государственного аэрокосмического университета. – 2011. – С 266 – 270.

