В данной работе представлены результаты исследований закона обратных квадратов. На примере закона всемирного тяготения логически проанализирован характер закона обратных квадратов. Экспериментальное подтверждение закона реализовано с помощью исследований интенсивности светового и воздушного потоков. Целью работы также являлось вовлечение студентов СПО в научную проектную деятельность; знакомство с планированием и организацией научных экспериментов, с методами обработки и оформления их результатов. Показано, что при наличии относительно простого оборудования (даже в домашних условиях) можно проводить достаточно серьезные физические эксперименты.
Ключевые слова: закон обратных квадратов, закон всемирного тяготения, гравитация, поток, интенсивность потока, освещенность, давление, люксметр, анемометр, ветромер, метод наименьших квадратов, MathCAD.
В качестве источника света использовался фонарик смартфона. Приемник (измеритель) — люксметр TASI TA8120, определяющий интенсивность светового потока (освещенность) до 10000 Лк.
Источником воздушного потока являлся бытовой вентилятор. Приемник (измеритель) — анемометр (ветромер) Benetech GM816, позволяющий измерять скорость газового потока до 30 м/с.
Для построения графиков использовался математический пакет MathCAD. Угловой коэффициент и свободный член в линеаризованных зависимостях рассчитывались с помощью метода наименьших квадратов.
Закон всемирного тяготения
На примере закона всемирного тяготения рассмотрим характер закона обратных квадратов [1]. Жизненный опыт (или знание второго закона Ньютона) подсказывает нам, что величина силы, требуемой для изменений в состоянии движения (покоя) тела массой m , пропорционально ее величине. Здесь речь, конечно, об инерционной массе. Однако, очевидно, что и для массы гравитационной (тождественной инерционной), такая зависимость справедлива. СилаF ГР притяжения между телами пропорциональна как массе первого тела m 1 , так и массе второго m 2 . Т. е. F ГР ~ m 1 и F ГР ~ m 2 . Обобщив, получаем, что
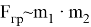
Данная пропорциональность не позволяет рассчитать значение силы, но помогает ответить, например, на вопрос: «Во сколько раз сила притяжения некоторого тела к телу массой 3 m больше силы притяжения к телу массой m ?». Из соотношения (1) следует ответ: «В три раза».
Сила притяжения зависит, очевидно, также и от расстояния
r
между телами и должна уменьшаться по мере увеличения расстояния между ними. Сила, таким образом, обратна пропорциональна расстоянию —
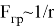
Волна, образовавшаяся на поверхности воды от брошенного камня, расходится от точки падения (центра волны) кругами. Энергия (кинетическая) камня, преобразованная в волну (энергию колебаний), распределяется по окружности радиуса r . Длина окружности равна 2π r . Чем дальше находится рассматриваемая точка от места падения камня, тем больше длина окружности, и, следовательно, меньше энергия колебаний в этой точке. Делаем вывод : воздействие обратно пропорционально расстояниюr .
Однако, гравитационное взаимодействие распределяется в пространстве во всех возможных направлениях (3D), а не в плоскости (2D). Рассмотрим следующую ситуацию. Пусть имеется точечный источник звука. Энергия, излучаемая источником (в виде звуковых волн), распределяется в этом случае по сфере радиуса r . Т. к. площадь S пропорциональна квадрату линейных размеров тела (для квадрата со стороной r — S=r 2 , для окружности радиуса r — S=πr 2 и т. п.), то плотность энергии, принесенной волной в данную точку пространства будет убывать обратно пропорционально квадрату расстояния от источника [2]. Таким образом, воздействие ослабевает пропорционально квадрату расстояния от точечного источника . Обобщив данный вывод на гравитационное взаимодействие, заключаем, что
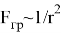
Объединив пропорциональности (1) и (2), получаем:
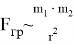
Таким образом, можно видеть, что гравитационное взаимодействие подчиняется закону обратных квадратов.
Проверка размерностей в соотношении (3) показывает, что коэффициент пропорциональности, который нужно в него ввести (чтобы «превратить его в полноценную формулу») должен иметь размерность Н·м 2 /кг 2 . Определить численное значение этого коэффициента теоретические невозможно, т. к. он является фундаментальной физической постоянной. Этот коэффициент определен экспериментально, равен G =6,67·10– 11 Н·м 2 /кг 2 , и называется гравитационной постоянной . В итоге закон всемирного тяготения имеет вид:

Закон обратных квадратов для светового потока
В данном разделе описаны результаты эксперимента по проверке закона обратных квадратов для светового потока, идущего от фонарика смартфона. Измерение интенсивности потока (освещенность) измерялась люксметром марки TASI TA8120. Схема эксперимента приведена на рисунке 1. Результаты измерений внесены в таблицу 1.
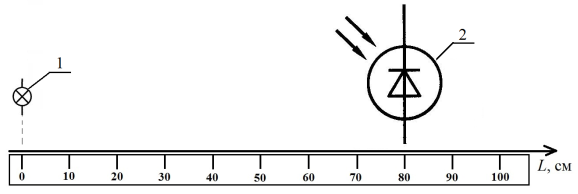
Рис. 1. Схема эксперимента по исследованию зависимости интенсивности светового потока (освещенности) от расстояния: 1 — источник света (фонарик смартфона), 2 — фотоприемник (люксметр)
Таблица 1
Результаты измерений
|
№ измерения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Расстояние L , см |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
Освещенность, Лк |
90,2 |
165,3 |
93,5 |
61,8 |
39,8 |
28,2 |
21,2 |
16,7 |
11,9 |
9,4 |
Сразу же обращает на себя внимание результат измерения при расстоянии между источником и приемником, равным 10 см. Он явно «выпадает» из общей тенденции к уменьшению освещенности при увеличении расстояния. Предполагается, что это связано с тем, что при таком близком расстоянии фронт светового потока падает не на всю «рабочую» поверхность фотоприемника, а только на его часть. Очевидно, каждая единица площади фоточувствительной поверхности люксметра обладает максимальным пороговым значением интенсивности светового потока на нее падающего. При малых расстояниях от источника площадь сферического светового фронта еще мала и освещенность превышает пороговые значения для данного люксметра, поэтому его показания оказываются меньше реальной величины интенсивности. В дальнейшем результат этого измерения при обработке учитывать не будем.
График зависимости светового потока от расстояния между источником и приемником представлен на рисунке 2.
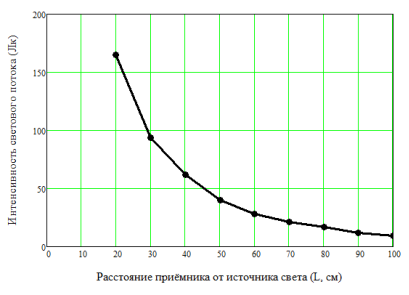
Рис. 2. Зависимость освещенности от расстояния между источником и приемником
Чтобы убедиться в справедливости закона обратных квадратов, необходимо построить график в координатах «интенсивность — обратный квадрат расстояния», т. е. график зависимости освещенности от 1/ L 2 (рис. 3).
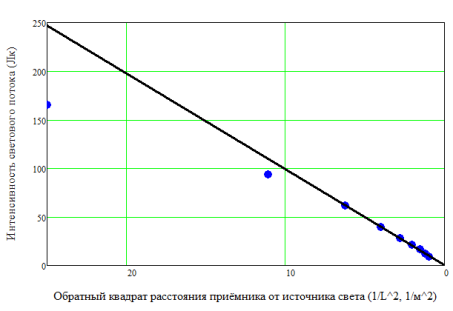
Рис. 3. Линеаризованный график зависимости освещенности от расстояния (угловой коэффициент и свободный член линейной зависимости, рассчитанные по методу наименьших квадратов, равны a =9,86 Лк·м 2 и b =0,43 Лк, соответственно)
Из графика (рис. 3) можно видеть, что экспериментальные точки, со значениями обратного квадрата меньше 10 (соответствует расстояниям от источника до приемника от 40 см и более), «укладываются» на прямую. Это означает, что, при расстояниях L приблизительно от 40 см и более, размером источника света можно пренебрегать (он становится материальное точкой, т. е. точечным источником) и начинает «работать» закон обратных квадратов.
Закон обратных квадратов для воздушного потока
Раздел содержит результаты исследования зависимости скорости воздушного потока от расстояния между его источником (вентилятор) и приёмником (анемометр Benetech GM816) (см. фото). Схема эксперимента представлена на рисунке 5. Результаты измерений внесены в таблицу 2.

Рис. 4. Источник и приёмник воздушного потока, измерение расстояние между ними
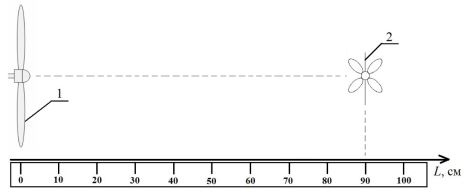
Рис. 5. Схема эксперимента по исследованию зависимости скорости газового потока от расстояния до источника: 1 — источник воздушного потока (вентилятор), 2 — анемометр (ветромер)
Таблица 2
Результаты измерений скорости воздушного потока при различных расстояниях
|
№ измерения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Расстояние L , см |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
Скорость потока, м/с |
3,5 |
3,3 |
3,1 |
2,5 |
2,2 |
1,8 |
1,6 |
1,5 |
1,4 |
1,2 |
График зависимости воздушного потока от расстояния между источником и приемником представлен на рисунке 6.
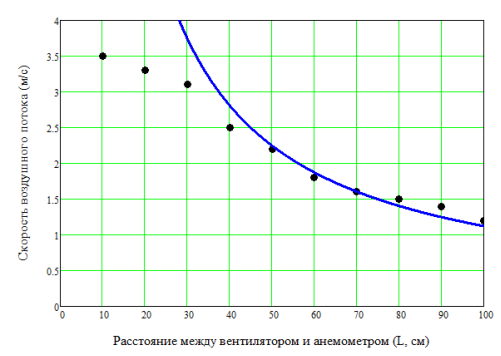
Рис. 6. Зависимость скорости потока от расстояния между источником и приемником
На графике (рис. 6) точками нанесены результаты экспериментальных измерений (табл. 2). Сплошной линией изображена аппроксимирующая кривая, о которой будет сказано ниже.
Можно видеть (рис.6), что с увеличением расстояния между источником и приемником скорость потока падает. Результат, конечно, очевидный и предсказуемый. Характер зависимости явно нелинейный. Проверка на линейность зависимости скорости v от обратного квадрата расстояния 1/ L 2 дала отрицательный результат (зависимость v от 1/ L 2 — нелинейная).
Конечно, при малых расстояниях вентилятор (источник газового потока) еще не нельзя считать материальной точкой (точечным источником). Однако, при расстояниях от 30 см и выше начинает наблюдаться некоторая закономерность в поведении зависимости (см. экспериментальные точки на рис. 6). Исследование показало, что зависимость скорости от расстояния при расстояниях от 30 см хорошо аппроксимируется зависимостью вида:
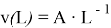
Для кривой, представленной на графике (рис. 6) А =0,89 м 2 /с.
Как объяснить подобную зависимость? Известно, что давление, создаваемое газами (вспомните, например, основное уравнение молекулярно-кинетической теории газов), пропорционально квадрату скорости молекул ( p ~ v 2 ). В данном случае давление, создаваемого воздушным потоком, должно быть пропорционально квадрату его скорости. С другой стороны, давление обратно пропорционально площади, по которой распределена его сила ( p ~1/ S ). Площадь же пропорциональна квадрату расстояния L 2 . Таким образом, давление обратно пропорционально квадрату расстояния ( p ~1/ L 2 ) и мы снова имеем дело с законом обратных квадратов .
Согласно сделанным выше рассуждениям, заключаем что скорость v должна быть пропорциональна L -1 . Это согласуется с ранее упомянутой хорошей аппроксимацией зависимости скорости о расстояния (см. график на рис. 6) функцией вида (5).
Чтобы окончательно убедиться в справедливости вывода о том, что скорость воздушного потока обратно пропорциональна расстоянию от его источника , проведем линеаризацию зависимости скорости от расстояния (на интервале от 40 см до 100 см). Воспользовавшись методом наименьших квадратов для связи переменных v и 1/ L , получили значения углового коэффициента a =0,856 м 2 /с и свободного члена b =0,402 м/с. График линеаризованной зависимости приведен на рис. 7.
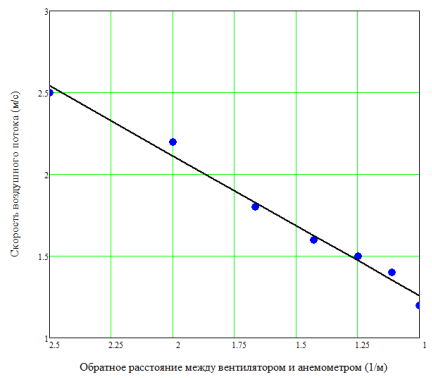
Рис. 7. Линеаризованная зависимость скорости потока от расстояния до источника
Можно видеть, что гипотеза о линейной зависимости скорости газового потока от обратного расстояния до источника подтвердилась. Следовательно, выполненные выше рассуждения о подчинении давления потока закону обратных квадратов справедливы.
Заключение
В ходе выполнения данной работы авторы (студенты) закрепили, полученные ранее [2], навыки
1) по планированию, организации и выполнению физических экспериментов;
2) использованию метода наименьших квадратов при линеаризации функциональных зависимостей;
3) оформлению результатов исследовательской работы в виде научной статьи.
Также студенты познакомились с такими физическими приборами, как люксметр и анемометр. Получили представление об аппроксимации как способе обработки массивов экспериментальных данных.
По результатам проведенных исследований можно сделать следующие выводы.
- При расстояниях от фонарика смартфона более 40 см его можно считать точечным источником света. Зависимость интенсивности светового потока (освещенности) от расстояния подчиняется в этом случае закону обратных квадратов.
- При расстояниях от бытового вентилятора более 40 см его можно считать точечным источником газового потока. Зависимость давления потока от расстояния подчиняется в этом случае закону обратных квадратов, а скорость потока уменьшается пропорционально увеличению расстояния.
Литература:
- Кириллов А. М. Методы решения физических задач [Электронный ресурс] // Фестиваль педагогических идей «Открытый урок». 2010. URL: http://festival.1september.ru/articles/587075/ (дата обращения: 11.02.2023).
- Кириллов А. М., Култышев А. Д., Григорьев. В. Ю. Распространение звука и звукоизоляция // Молодой ученый. — 2023. — № 3 (450).

