Переменные, входящие в состав модели общего вида, удобно группировать и рассматривать по трем основным признакам:
1) с точки зрения роли, которую они играют по отношению к объекту моделирования;
2) c точки зрения характера и механизмов их изменчивости;
3) с точки зрения их информативности, прежде всего наблюдаемости и возможности измерения.
Основные типы переменные, упорядоченные в соответствии с этими тремя признаками, представлены на схеме (рис.1).
Входные и выходные переменные, как мы уже выяснили выше, характеризуют учитываемые в модели связи среда- объект и объект — среда соответственно. В прямых модельных задачах, когда по данным о входах и внутренних свойствах объекта исследуется его «поведение» в тех или иных условиях и режимах, входные переменные представляют собой главный результат решения задачи. Иногда задача модельного исследования ставится иначе: входные и выходные переменные наперед известны (доступны для измерения и исследования), а определению подлежат неизвестные внутренние свойства, в общем случае- структура и параметры объекта моделирования. Этот класс обратных задач, которые принято характеризовать как задачи идентификации объекта, мы рассмотрим ниже в отдельной главе.
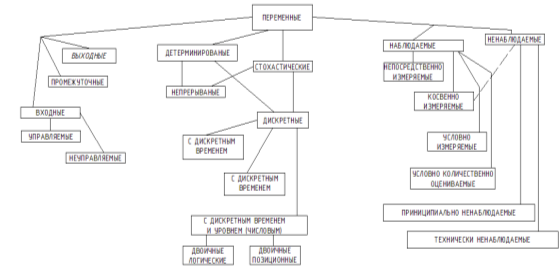
Рис. 1. Основные классы модельных переменных
Помимо входных и выходных на рис.1 выделены в отдельный класс промежуточные переменные (в дальнейшем они будут обозначаться буквой у), которые характеризуют связи между компонентами объекта в тех случаях, когда в модели учитывается сложная внутренняя структура последнего, например в иерархических системах.
Входные переменные разделяются на два существенно различных подкласса рис.2: управляемые, или управления (и), и неуправляемые или возмущения (U).
Значения первых в принципе поддаются целенаправленному изменению, позволяя, таким образом, воздействовать на объект и приближать его состояние к желаемому или оптимальному по некоторому критерию.
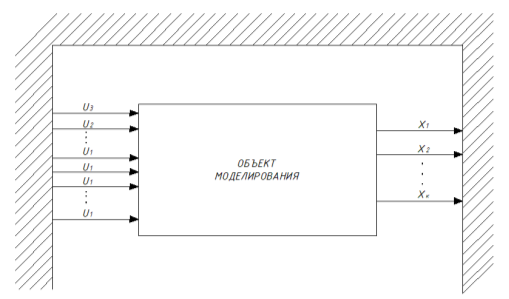
Рис. 2. Объект моделирования и среда.
Естественно, что для реализации этой возможности необходим, вообще говоря, лежащий вне объекта специальный орган управления, который формирует управляемые переменные и совместно с объектом, прямыми и обратными связями, а также вспомогательными техническими средствами (датчиками и др.), образует систему управления.
Неуправляемые входные переменные изменяют свои значения состояния объекта. Характеристики возмущающих переменных часто носят стохастический характер и поддаются оцениванию только на вероятностной мере. Поэтому исследование и описание возмущающих переменных в процессе построения модели представляет собой не только ответственную, но часто и достаточно сложною задачу, связанную с необходимостью проведения специальных экспериментов, сбора и статистической обработки больших объемов исходных данных.
Весьма существенно деление возмущающих переменных на наблюдаемые и ненаблюдаемые воздействиям, однако первые могут быть наблюдены, измерены, а, следовательно, и непосредственно скомпенсированы соответствующими изменениями управляющих воздействий (так называемое управление по возмущениям). Вторые, по принципиальным или техническим причинам недоступные для наблюдения и контроля, проявляют себя только через изменения состояний объекта. Компенсация ненаблюдаемых возмущений в принципе возможно только опосредованно, в системах управления с обратными связями.
Характеристики изменчивости модельных переменных достаточно пестры и многообразны. Однако важнейшим признаком, определяющим возможные методы исследования и описания, а также адекватные математические образы и аппарат, является деление переменных на детерминированные и стохастические.
По существу, на этих предложениях, обеспечивающих возможность формализованного статистического описания случайной величины или процесса, зиждется все информационное «качество» стохастических модельных переменных — степень достоверности их усредненных характеристик. В то же время общих методов, которые позволяли бы априорно убедиться в статистической устойчивости и стационарности подлежащего исследованию и описанию реального случайного процесса, не существует.
В некоторых случаях, например в задачах молекулярной и ядерной физики, в ряде задач радиотехники и теории связи, в статистической звездной астрономии, постулировать стационарность удается, исходя из практически достоверных теоретических соображения, основанных главным образом на законе больших чисел.
Литература:
- Неуймин Я. Г. Модели в науке и технике. История, теория, практика. — Л.: Наука, 1984. — 189 с.
- Эгамов Н. М. О методах моделирования и модельных представлений. Молодой ученый: Ежемесячный научный журнал. — Казань, 2016. — 8 (112). — С.363–365.

