Рассмотрим класс человеко-машинных (эргатических) систем [1…4], описываемых уравнениями движения:
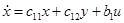
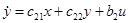 ;
;
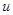 - управляющие движения оператора [5] (для короткопериодической составляющей продольного движения самолета
- управляющие движения оператора [5] (для короткопериодической составляющей продольного движения самолета 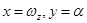 ).
).
В конечных разностях имеем:
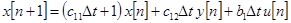
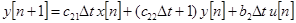 ,
,
или:
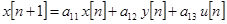
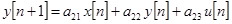 .
.
где 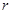 - число измерений
- число измерений 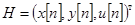 .
.
Параметры, доставляющие минимум функционалам качества [1] 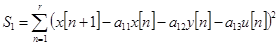 и
и 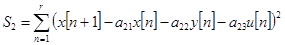 , определятся из систем уравнений в матричной форме соответственно:
, определятся из систем уравнений в матричной форме соответственно:
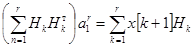 , (1)
, (1)
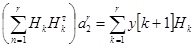 , (2)
, (2)
где
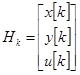
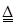
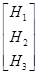 ,
, 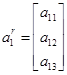 ,
, 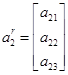
(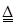 — равенство по определению).
— равенство по определению).
Введем
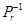
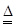
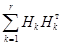 , (3)
, (3)
Тогда из (1) следует:
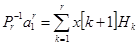 ,
, 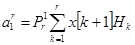 ; (4)
; (4)
а из (4) и (1):
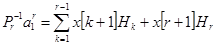 , (5)
, (5)
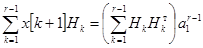 .
.
Справедливо:
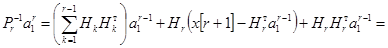
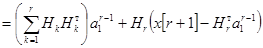 .
.
Последняя формула легко приводится к виду
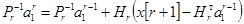 .
.
Получим рекуррентную формулу для оценки 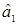 при r-ом измерении через оценку при (r-1)-ом измерении
при r-ом измерении через оценку при (r-1)-ом измерении
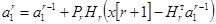 . (6)
. (6)
Аналогично получили бы формулу для оценки 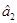 :
:
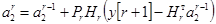 . (7)
. (7)
Оценку 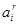 можно получить рекуррентно по предыдущей оценке
можно получить рекуррентно по предыдущей оценке 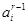 и по измерениям
и по измерениям 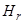 ,
,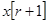 , если матрица
, если матрица 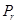 так же получена последовательно.
так же получена последовательно.
По (3) имеем:
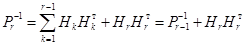 . (8)
. (8)
Пусть известно начальное значение матрицы 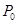 .
.
Тогда, умножая (8) слева на 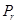 , получим:
, получим:
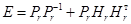 ; (9)
; (9)
а умножив на 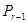 (9) справа, получим:
(9) справа, получим:
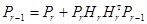 . (10)
. (10)
Из(10), умножая на 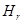 справа, получим:
справа, получим:
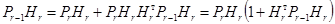 .
.
Умножая далее справа на 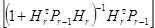 , получим:
, получим:
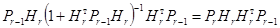 . (11)
. (11)
Подставив 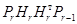 в (10) из (11), получим
в (10) из (11), получим
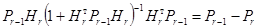 .
.
Таким образом, получили окончательный вид рекуррентной формулы:
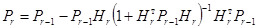 . (12)
. (12)
(принималось 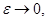
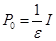 ; вообще говоря, начальная оценка может быть произвольной).
; вообще говоря, начальная оценка может быть произвольной).
При расчетах использовалась формула (11) в развернутом виде:
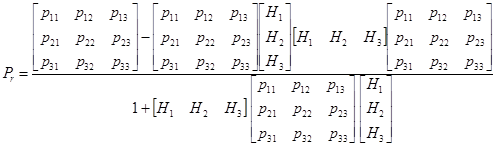 .
.
Алгоритм идентификации непосредственно вытекает из соотношений
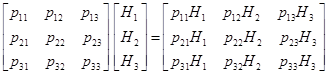
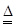
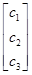 ,
,
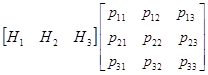
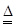
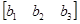 ,
,
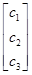
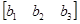
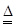
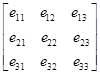 ,
,
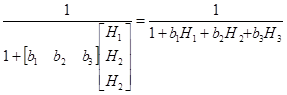
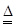 q.
q.
Приведенный алгоритм широко и эффективно использовался при разработке тренажных и обучающих комплексов для различных отраслей промышленности [5…7]. Для рассматриваемого класса систем можно принять:
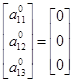 ,
, 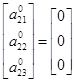 ;
; 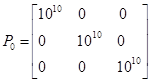 .
.
Литература:
1. Авиационные тренажеры модульной архитектуры: монография; под редакцией Лапшина Э. В., д.т.н., проф. Данилова А. М. — Пенза: ИИЦ ПГУ. — 2005. — 146 с.
2. Планирование эксперимента. Обработка опытных данных: монография / И. А. Гарькина [и др.]; под ред. проф. А. М. Данилова. — М.: Палеотип. — 2005. — 272 с.
3. Данилов А. М., Гарькина И. А. Сложные системы: идентификация, синтез, управление. — Пенза: ПГУАС. — 2011. — 308 с.
4. Данилов А. М., Гарькина И. А., Домке Э. Р. Математическое и компьютерное моделирование сложных систем. — Пенза: ПГУАС. — 2011. — 296 с.
5. Данилов А. М., Домке Э. Р., Гарькина И. А. Формализация оценки оператором характеристик объекта управления / Известия ОрелГТУ. Информационные системы и технологии. — 2012. — № 2 (70). — С.5–11.
6. Хнаев О. А., Данилов А. М. Методы планирования эксперимента в аппроксимации функций многих переменных / Молодой ученый. — 2014. — № 4. — С.295–297.
7. Будылина Е. А., Гарькина И. А., Данилов А. М., Пылайкин С. А. Аналитическое определение имитационных характеристик тренажных и обучающих комплексов // Фундаментальные исследования. — 2014. — № 6 (часть 4). — С. 698–702.

