Математическое моделирование динамических систем является естественным и одним из основных способов их изучения. Усложнение задач анализа динамики систем и расширение класса исследуемых динамических объектов требуют последующего развития и усовершенствования методов математического моделирования, разработки новых эффективных методов и средств компьютерной реализации математических моделей реальных физических объектов и процессов.
В процессе решения задач динамики, в том числе при исследовании и проектировании динамических систем, важным методом проявления их специфических свойств и возможностей численной реализации является представление моделей в различных близких друг другу формах, что приводит к необходимости поиска и развития методов эквивалентного преобразования моделей. Часто получение модели, исходя из ее физических свойств, удобно в одной форме, а ее численная реализация в другой, эквивалентной исходной.
Следующим этапом после определения оптимального типа математической модели и приведения ее к виду удобному для моделирования на ЭВМ, является собственно ее компьютерная реализация.
Пусть задана задача Коши для дифференциального уравнения с переменными коэффициентами
(1)
она имеет эквивалентное представление в виде интегрального уравнения [1]
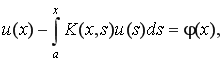
где
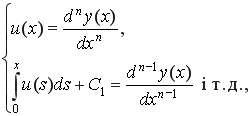(2)
,
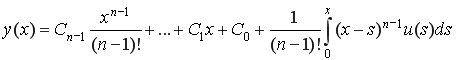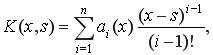(3)
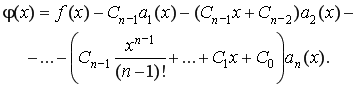
При получении данных выражений выполняется интегрирование выражений (2) и используется формула
.
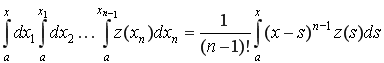Можно увидеть, что задача (1) эквивалентна интегральному уравнению Вольтерра ІІ рода с частичным видом ядра (3). Выбор одной из двух эквивалентных форм записи задачи Коши зависит от самой постановки решаемой задачи и от ее свойств при численном решении.
Одной из лучших форм описания динамических систем являются интегро-дифференциальные уравнения, однако их анализ является одной из наименее исследованных областей математического моделирования. Во время применения интегро-дифференциальных моделей важное прикладное значение для исследователя имеет их эквивалентное аналитическое преобразование к моделям в виде интегральных уравнений, методы численной реализации которых достаточно хорошо разработанные и имеют ряд преимуществ: стойкость решения, меньшую чувствительность от возмущений, погрешностей входных данных и т. д. Кроме того, такое преобразование позволяет расширить класс используемых численных методов, в частности, позволяет использовать быстросходимые итерационные методы и методы владеющие высокой стойкостью решения интегральных уравнений, например, модифицированный метод Ньютона-Канторовича [2]. Рассмотрим нелинейное интегро-дифференциальное уравнение вида [3]:
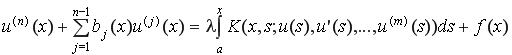, (4)
с нулевыми начальными условиями
,
и 
— непрерывные функции, 
.
Пусть 
— фундаментальная система решений однородного дифференциального уравнения
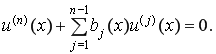
Тогда общее решение неоднородного дифференциального уравнения
,
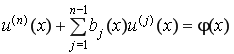можно записать в виде
.(5)
Согласно метода вариации постоянных, коэффициенты определяются за формулой [4]
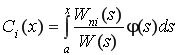, (6)
где
,
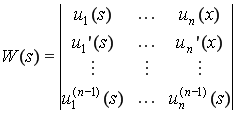— минор элемента 
-ой строки 
-го столбца определителя 
.
С учетом (6) выражение (5) примет вид
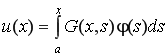, (7)
где
, 
.
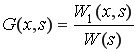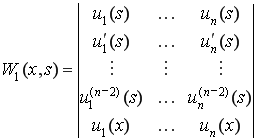Учитывая выражение (7), уравнение (4) можно привести к виду [5]:
,
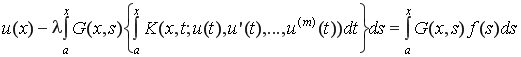а потом, выполнив замену 
, преобразовать к эквивалентному интегральному уравнению
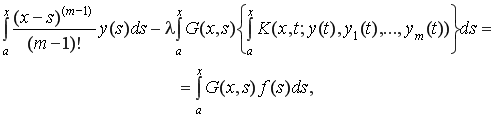
где
.
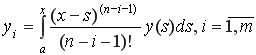В случае ненулевых начальных условий 
, заменой переменных
,
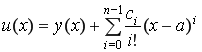задача сводится к задаче с нулевыми условиями.
Переход от интегральных уравнений к дифференциальным, как один из подходов к решению линейных и нелинейных интегральных уравнений Вольтерра, возможен лишь в частичном случае, что являются следствием высокой универсальности уравнений Вольтерра ІІ рода как формы описания задачи Коши. Одним из таких частичных, но распространенных случаев является случай вырожденного, или близкого к нему, ядра. Такой подход может быть вполне аргументированным как при математической постановке задачи, так и при их развязывании, поскольку методы развязывания дифференциальных уравнений достаточно хорошо разработанные и широко применяются.
При решении практических задач часто представляется удобным приближенно заменять дифференциальные уравнения в частных производных дифференциальными уравнениями в обыкновенных производных. Это представляется возможным при использовании метода конечных разностей или как его часто называют метод прямых, а также при помощи методов, основанных на замене функций многих переменных суммой произведений функции, каждая из которых представляет функцию только одной переменной.
Использование эквивалентных форм математических моделей динамических систем является общепринятым подходом. Рассмотренные в работе методы позволяют получать модели, исходя из ее физических свойств, в одной форме, а ее численную реализацию проводить в другой, эквивалентной исходной.
Литература:
- Верлань А. Ф., Сизиков В. С. Интегральное уравнение: Методы, алгоритмы, программы. — К.: Наукова думка, 1986. — 542 с.
- Канторович Л. В., Акилов Г. П. Функциональный анализ, второе издание. — М.: Наука, 1977. — 744 с.
- Верлань А. Ф. Некоторые особенности интегрального метода математического моделирования / А. Ф. Верлань // Электроника и моделирование, 1975, вып. № 5, С. 82–86.
- Бенькович Е. С. Практическое моделирование сложных динамических систем / Е. С. Бенькович, Ю. Б. Колесов, Ю. Б. Сениченков — СПб.: БХВ, 2001. — 401 с.
- Верлань А. Ф. Математическое моделирование непрерывных динамических систем / А. Ф. Верлань, С. С. Москалюк. — К.: Наук. думка, 1988. — 287 с.
