Методы и технологии моделирования технических систем
Даненова Гульмира Тулендиевна, кандидат технических наук, доцент;
Зияшева Айжан Манарбековна, магистрант;
Альжанова Алмагуль Ураловна, магистрант;
Жарилхасинова Динара Кунисбаевна, магистрант
Карагандинский государственный технический университет (Казахстан)
Компьютерное моделирование осуществляется в различных формах и термин приобрел много значений в различных областях. Родственным термином, который часто используется взаимозаменяемо с компьютерной симуляцией является компьютерное моделирование. Вообще говоря, компьютерная симуляция является широким термином, который включает в себя практику получения входов от имитируемых пользователей, а затем передать эти значения в реальные компьютерные программы (эту практику иногда называют эмуляцией). Например, летныесимуляторы могут имитировать полетные операции,контролируя фактический перелет программного обеспечения. Компьютерное моделирование сужает область применения и включает в себя все аспекты системы представленые с помощью компьютера.
Компьютерные симуляторы успешно используются во многих областях, включая инженерию, производство, менеджмент, бизнес, науку, технологию, архитектуру, развлекательный, правительственный, военные области и область логистики/транспортировки. Несколько типов компьютерного моделирования широко изучены для использования в инженерных и бизнес-средах. Они включают в себя непрерывное, Монте-Карло, дискретно-событийное и агентное моделирование. Хотя многие представители власти считают дискретные события в виде симулятора Монте-Карло, они будут оцениваться отдельно, поскольку, как показывает практика, каждое из них рассматривается индивидуально и для разных приложений.
Непрерывное моделирование
Непрерывное моделирование относится к моделированию системы уравнений, представляющей систему, работающую в течение долгого времени. Эта система может состоять из алгебраических систем, теоретико-игровых моделей, статистических моделей или дифференциальных уравнений, установленных таким образом, чтобы изменить непрерывное представление входных и выходных параметров, связанных с состоянием системы. Примером непрерывного моделирования является модель полноприводной системы подвески, в которой может быть исследована динамика работы над различными местностями.
Непрерывное моделирование часто используется в сочетании с АР (Автоматизированная разработка) систем или в математическом моделировании пакетов программного обеспечения.
Другим примером непрерывного моделирования является модель конкуренции двух популяций. Биологические модели этого типа известны в качестве моделей хищник-жертва. Среда состоит из двух популяций, которые взаимодействуют друг с другом. Хищники зависят от добычи в качестве источника пищи. Если количество хищников растет слишком быстро, добыча будет уменьшаться, а хищники будут голодать. Если количество хищников падает, количество добычи будет увеличиваться. Эта взаимосвязь может быть проанализирована непрерывным моделированием с использованием частных производных. Математика этой системы двух видов была разработана известным теоретиком Вольтерром. Он показал, что без внешнего вмешательства, результатом будет пульсирующее отношение похожее на график показанный на рисунке 1.
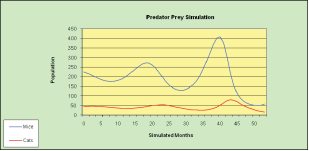
Рис. 1.Имитационная модель «хищник-жертва»
Рост населения, рост городов, прогнозирование ураганов и погоды, распространение болезни являются подходящими примерами систем для непрерывных имитационных моделей. Термин «динамика системы» впервые использованный Джей У. Форрестером в 1950, также используется, чтобы описать непрерывное имитационное моделирование. В общем, динамика системы описывает поведение системы, как взаимосвязаные, взаимодействующие обратные связи, каждый из которых может прямо или косвенно повлиять на другой.
Непрерывные симуляторы обычно разработаны с использованием электронных таблиц, специализированного математического программного обеспечения как MATLAB или Mathematica, специализированного программного обеспечения моделирования Simulink MATLAB, либо разработаны с использованием традиционных языков программирования, таких как Visual Basic или C ++. [1, с. 15]
Моделирование Монте-Карло
Название Монте-Карло вызывает мысли об играх, азартных играх и шансе. Джон фон Нейман использовал кодовое название «Монте-Карло» для своих опытов, основанных на использовании случайных чисел, проведенных в Лос-Аламосе во время первоначальной разработки атомной бомбы. Название стало популярным и сейчас используется, чтобы представить результаты моделирования, как «схему с использованием случайных чисел, которая используется для решения некоторых стохастических или детерминированных задач, в которых ход времени не играет никакой роли».Последняя часть этого определения (например, определения временем) отличает Монте-Карло от дискретно-событийного моделирования. Монте-Карло вообще исключает время из модели, тогда как дискретно-событийное моделирование основано на течении времени. Использование генераторов случайных чисел дает моделированию методом Монте-Карло характеристики не распространенные для непрерывного моделирования.
Рассмотрим следующее моделирование игры пейнтбола написанное в форме моделирования методом Монте-Карло.
Эта модель предсказывает число красных и синих членов команды,чтобы выжить в матче с учетом предположений, перечисленных ниже:
1) Матч проводится на дальней дистанции. Любой пейнтболист может попасть в случайно выбранного противника с одинаковой легкостью.
2) Нет двух пейнтболистов выбирающих одну и ту же цель.
3) Матч продолжается, пока одна сторона полностью не уничтожена или пока не выстрелено 100 шаров.
4) Каждый пейнтбольный шар, который попадает в члена команды соперников убирает его из конкурентов.
5) В контексте моделирования методом Монте-Карло, весь матч проходит в нулевом имитируемом времени.
6) Вероятность того, «какая сторона следующая выстрелит шарами» базируется на процентах красного и синего членов команды, которые в настоящее времяактивны и являются частью матча.
7) Размеры начальной команды разнообразны и записаны.
8) Средние размеры завершения команды базируются на 1000 матчах.
Модель может быть запущена на 1000 матчей для каждого из сценариев. Чем больше количество запусков, тем ближе количество оставшихся игроков будет сходиться к точному решению. Значением этого типа моделирования является то, что несколько минут работы на компьютере дает ответ, который будет сложно оценить в реальной жизненной ситуации. Еще одно преимущество присущее этой имитации является та легкость, с которой параметры могут быть изменены и запущены в различных экспериментах.
Дискретно-событийное компьютерное моделирование
Дискретно-событийное моделирование характеризуется прохождением блоков времени, в течение которых ничего не происходит, перемежаются события, которые изменяют состояние системы. Примером может служить простая система очереди, состоящая из клиентов банкомата. Клиенты приходят, если банкомат находится в использовании, ждут обслуживания, получают услугу, а затем уходят. Могут быть сделаны следующие предположения:
- Прибывающие клиенты ждутперед банкоматом (если он используется) в одной очереди.

-
 Время между прибывающими:
Время между прибывающими:
|
1 мин |
5 % прибывающих |
6 мин |
20 % прибывающих |
|
2 мин |
7 % прибывающих |
7 мин |
10 % прибывающих |
|
3 мин |
8 % прибывающих |
8 мин |
8 % прибывающих |
|
4 мин |
10 % прибывающих |
9 мин |
7 % прибывающих |
|
5 мин |
20 % прибывающих |
10 мин |
5 % прибывающих |
- Время обслуживания банкоматом:
|
1 мин |
10 % прибывающих |
4 мин |
25 % прибывающих |
|
2 мин |
25 % прибывающих |
5 мин |
10 % прибывающих |
|
3 мин |
30 % прибывающих |
Моделирование может быть написано в GPSS World, который является дискретно-событийным языком моделирования Minuteman Software.
Целью данного моделирования является определение максимальной длины очереди клиентов, среднее время ожидания обслуживания, и время использования банкомата в процентах.
Моделирование будет выполняться в течение1000 часов моделируемого времени.
Если процент использования имитации банкомата будет близок к 100 %, определяется необходимость установки дополнительного банкомата. Это моделирование также можно перенастроить для определения работы банкомата в пиковые моменты. Например, если в пятницу на крупном близлежащем заводе был день зарплаты, может ожидаться большой приток клиентов банкомата. Данные показывающие такой приток могут быть введены в имитационную модель и проанализированы для оценки влияния на коэффициент использования банкомата и времени очереди. [2, с. 35]
Агентное Моделирование
Агентное моделирование рассматривает одновременно взаимодействия нескольких агентов для имитации, воссоздания, изучения и прогнозирования сложного явления. Понятие агентного моделирования заключается в том, что в целом поведение возникает через взаимодействия отдельных агентовна микроуровне. Основным предположением является то, что простые местные поведения генерируют поведения сложного верхнего уровня. Индивидуальные агенты моделируются с учетом индивидуальных особенностей и их, как правило, принято считать рациональными, действущими в своих собственных интересах, которые могут быть экономического или социального происхождения. Модель будет использовать локальные эвристики и простые правила принятия решений, которые создают более широкое окружение.
Большинство агентных моделей содержит следующие элементы:
- несколько агентов смоделированных и масштабированных с различными уровнями детализации (гранулярности)
- правила и эвристики принятия решений
- адаптивное поведение или обучение
- правила или топология взаимодействия
- среда для взаимодействия, часто состоящая из ограниченных ресурсов
Агентное моделирование, начало набирать популярность в 1990-х годах и нашла применение в различных бизнес, социальных и технических областях. Агентные модели были применены для подачи цепных проблем потребительского поведения, социального взаимодействия, управления персоналом, анализа фондового рынка, пандемии групповых моделей, схем движения, и т. д.
Рассмотренные типы компьютерного моделирования широко изучаются и используются в инженерных и бизнес-средах
Литература:
- Understanding computer simulation. Roger McHaney. — 2009.
- Шеннон Р. Имитационное моделирование систем. Искусство и наука. — М.: Мир, 1978
- Технология системного моделирования / Под ред. С. В. Емельянова. — М. 1989.

