Группа аналитических математических моделей чрезвычайно обширна и разнообразна. Она включает в себя огромное множество абстрактных математических объектов вместе с операциями, определенными над этими объектами: все виды функциональных зависимостей, алгебраические, дифференциальные и интегро-дифференциальные уравнения с их конечноразностными эквивалентами, векторы и векторные пространства, матричные формы, тензоры и т. д. Вместе с тем принадлежность модели к этой группе предполагает, что не только описание объекта моделирования, но и весь процесс его исследования осуществляется аналитическими методами, т. е. в общем виде, а не численно: интегралы берутся в квадратурах, дифференциальные уравнения имеют решения, в форме функциональных зависимостей и т. д. Подобное требования является весьма жестким: на опыте хорошо известно, что прикладная задача, поддающаяся хотя бы не вполне строгому (с аппроксимацией функций конечными рядами и другими допущениями), но общему решению, представляют собой чрезвычайно приятное, что столь же редкое исключение из общего правила. До появления ЭВМ -это обстоятельство служило главным препятствием для решения математическими методами огромного большинства прикладных задач, ибо заставляло исследователя идти на такие упрощения, при которых вместе с водой выплескивается из ванной и ребенок. Сегодня эта ситуация в корне изменилась. Невозможность или просто излишняя сложность аналитического решения модельной задачи означает лишь необходимость перейти к численным методам математического исследования с использованием ЭВМ и соответственно преобразовать аналитическую математическую модель в алгоритмическую (численную).
Группа алгоритмических моделей, либо получаемых в результате преобразования из аналитических форм, либо получаемых в результате преобразования из аналитических форм, либо синтезируемых непосредственно, представляет собой наиболее универсальное средства математического моделирования. Единственным практически важным ограничением здесь является размерность модельной задачи, которая должна соответствовать возможностям (памяти, быстродействию и другим характеристикам) используемой ЭВМ. С учетом указанного ограничения и некоторых дополнительных требования в части математической корректности задачи (например, при обращении плохо обусловленных матриц) алгоритмические модели в принципе допускают решение любых, в том числе существенно нелинейных, модельных задач, но только в численной форме. При этом каждый прогон, или результат применения алгоритма к исходным данным, дает информацию о каком- то одном, вполне конкретном состоянии объекта. Для того чтобы исследовать объект при различных значениях параметров, начальных и граничных условий, внешних воздействий и т. п. необходимо столько повторений вычислительного процесса, сколько точек, характеризующих возможные состояния объекта, мы считаем необходимым получить. Поэтому реализация численной алгоритмической модели, вообще говоря, требует несравненно большего объема вычислительной работы, чем любая аналитическая модель, позволяющая исследовать свойства и характеристики объекта в общем виде, т. е. сразу во всех возможных состояниях. Эта особенность численных моделей носит принципиальный характер и может рассматриваться как своего рода плата за их универсальность. К счастью, в наше время сложность модельного алгоритма, громоздкость и большой объем вычислений, необходимых для исследования модели, как правило, не является серьёзным препятствием. Современные ЭВМ с их техническими возможностями, а также совершенные системы программно- математического обеспечения ЭВМ, автоматизирующие не только сам вычислительный процесс, но и процедуры его программирования, позволяют успешно решать подавляющее большинство возникающих в науке и практике модельных задач, которые поддаются математической формализации. Именно это обстоятельства служит главным стимулом исключительно высоких темпов развития и все более широкого распространения методов математического моделирования. Есть все основания полагать, что и впредь в обозримой оставаться самым универсальным и потому наиболее популярным подклассом вполне формализованных моделей.
Информационные модели, относящиеся к последней группе подкласса вполне формализованных моделей, в настоящее время также весьма многочисленны и разнообразны как по характеру задач (информационного-поисковые системы различных видов, банки данных, АСУ и др.), так и с точки зрения используемых специальных информационно-логических языков (ЛИСП, «Симск-рипт», «Симула», «Кобол» и т. п.). Общей особенностью информационных моделей являются относительно несложные, главным образом логического характера алгоритмы (такие как поиск и выборка данных по некоторым признакам, всевозможные сортировки данных, актуализация информации и др.), которые осуществляются над очень большими по объему массивами данных. Информационные модели, как правило, достаточно узко специализированы, в связи с чем далее они не рассматриваются. Подробные сведения о моделях этой группы можно найти в специальной литературе, в настоящее время уже весьма обширной.
Особое место среди идеальных моделей занимают показанные в правой нижней части рисунка и получившие развитие лишь в последние годы комбинированные модели, которые мы выше условно назвали эвристикой-алгоритмическими имитационными.
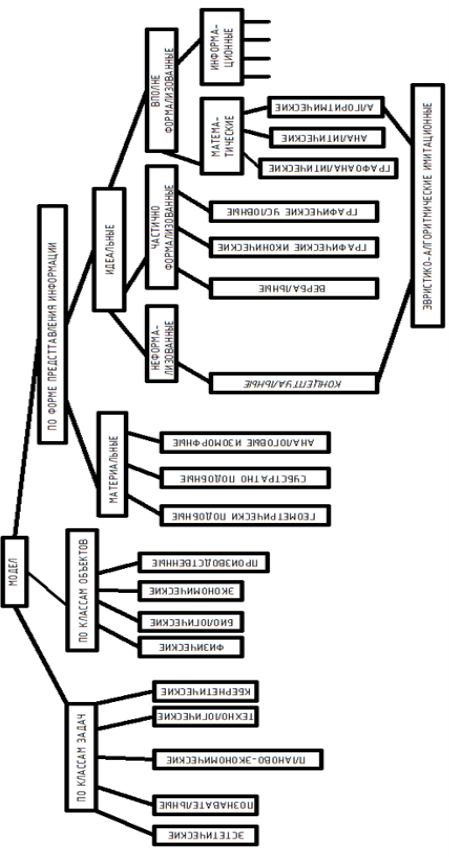
Рис. Основы классификации моделей
Алгоритмические математические модели, предусматривающие реализацию в численной форме с помощью ЭВМ, универсальны в том смысле что в силу абстрактности математических образов и методов не связаны с конкретной природой моделируемых объектов. Однако в информационном отношении возможности моделей этого класса не безграничны. Во-первых, исследуемый объект (процесс) должен поддаваться если не целостному, то хотя бы поэлементному математическому описанию, что влечет за собой требования достаточной изученности объектов и полноты исходной информации. Во-вторых, как мы уже отмечали выше, в ряде исследовательских и прикладных модельных задач их размерность и сложность превосходит возможности не только современных, но и перспективных ЭВМ. Наконец, существуют алгоритмического моделирования неприменима.
Ограниченные возможности алгоритмических математических моделей, как мы отмечали выше, в главе 1, стали особенно заметно проявляться на практике в последние десятилетие — полтора, когда жизнь выдвинула на первый план целый ряд системных задач, связанных с производством, экономикой, рациональным использованием ресурсов, социальной экологией и др., причем не только оптимальное но хотя бы удовлетворительное решение каждой из них практически неисчерпаемых творческих возможностей человеческого мозга с информационного — вычислительными возможностями современных ЭВМ, которое реализуется в так называемых диалоговых человеко- машинных системах, обеспечивающих непосредственный оперативный контакт и «общение» между человеком исследователем и информационно-вычислительной системой. Таким образом, мы являемся свидетелями рождения принципиально нового, чрезвычайно интересного в методологическом отношении типа человеко- машинных моделей, подробное рассмотрение которых выходит за рамки этой работы. На рисунке нашли отражение не все классификационные признаки моделей. За пределами схемы и нашего рассмотрения осталось подразделение моделей на статические (квазистатические) и динамические, на непрерывные, непрерывные дискредитированные и дискретные, на жестко детерминированные и стохастические.
Литература:
- Неуймин Я. Г. Модели в науке и технике. История, теория, практика. — Л.: Наука, 1984. — 189 с.
- Эгамов Н. М. О методах моделирования и модельных представлений. Молодой ученый: Ежемесячный научный журнал. — Казань, 2016. — 8 (112). — С.363–365.

