Математическая модель САР скорости системы «АИН ШИМ - линейный асинхронный двигатель»



Математическая модель САР скорости системы «АИН ШИМ - линейный асинхронный двигатель»

Емельянов Александр Александрович, доцент;

Бесклеткин Виктор Викторович, ассистент;

Прокопьев Константин Васильевич, студент;

Ситенков Александр Александрович, студент;

Бурхацкий Владимир Владимирович, студент;

Мальцев Никита Васильевич, студент

Российский государственный профессионально-педагогический университет (г. Екатеринбург)

Главной целью данной работы является использование идеи векторного управления для линейного асинхронного двигателя (ЛАД) в доступной для понимания студентами форме. Поэтому, вначале рассмотрим главный канал системы без обратных связей (рис. 1).

Целесообразно выделить 10 уровней, так как в некоторых из них имеются повторяющиеся элементы с одинаковой структурой программ.

Программирование каждого уровня с одним или множеством элементов производим в Script таким образом, чтобы каждые последующие продукты программ включали предыдущие. В этом случае мы увидим процесс влияния элементов предыдущих уровней на результаты последующих. Только имея представление о роли каждого элемента в главном канале можно переходить к завершающей стадии – введению обратных связей. В основу данной работы положены математические модели линейного асинхронного двигателя, рассмотренные в работах [1] и [2].

Из многочисленных публикаций по векторному управлению, на наш взгляд, необходимо отметить работы [3], [4], [5]. Кроме того, необходимо рассмотреть все наши статьи за последний год, относящиеся к данной теме.

Элементы системы управления (ЗИ, фильтры, регуляторы) «привязаны» к вращающейся системе координат, а математическая модель линейного асинхронного двигателя к неподвижной трехфазной системе индуктора, поэтому здесь необходимо обеспечить двухэтапное преобразование напряжений:

 u_x, u_y → u_α, u_β – из вращающейся системы, связанной с циклической частотой питающего напряжения к неподвижной декартовой системе α, β;

 u_α, u_β → U_a, U_b, U_c – из неподвижной системы α, β переход к трехфазной системе a, b, c.

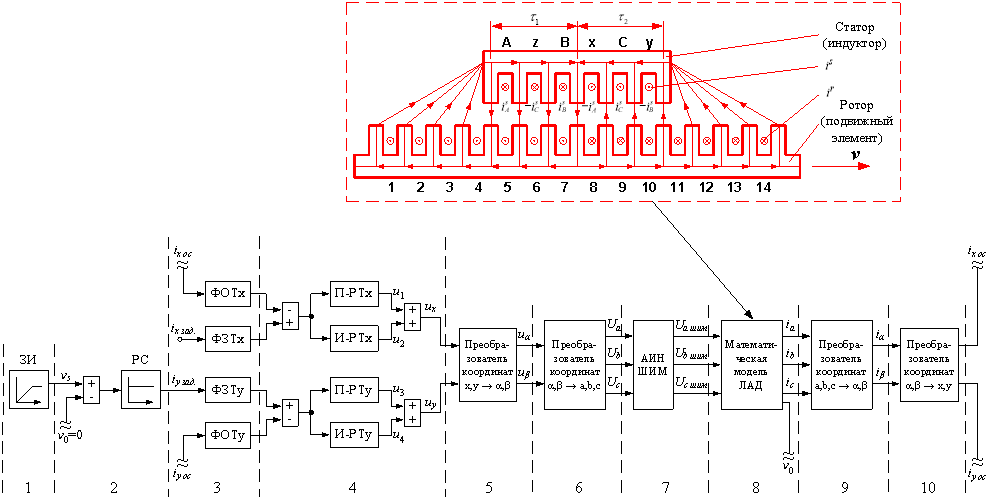Рис. 1. Главный канал разомкнутой системы

Далее токи i_a,b,c линейного асинхронного двигателя проходят также двухэтапное преобразование: i_a,b,c → i_α,β и далее i_α,β → i_xoc,yoc. Сигналы i_xoc, i_yoc далее в замкнутой системе уже можно подать на сравнивающие устройства с сигналами задания.

Циклическая частота вращения системы координат равна циклической частоте подаваемого напряжения на двигатель, т.е. ω_к = ω_s. Связь циклической частоты ω_к = ω_s с линейной скоростью поля .

Поэтому наиболее перспективным представляется рассмотрение следующей схемы: все процессы в отношении к циклической частоте ω_к = ω_s, в том числе задатчик интенсивности, задавать не в системе v_s = f(t), а в системе ω_к = ω_s = f(t), но тогда линейную скорость подвижной части необходимо преобразовать в ω = f(v₀). На выходе математической модели ЛАД необходимо установить преобразователь линейной скорости в циклическую ω = ω_s∙(1-s), где .

Тогда все регуляторы рассчитываются по классическим формулам для векторных систем с АД [3], [4], [5]. Причем за базовую принимаются паспортные данные асинхронного двигателя с близкими по характеристикам к ЛАД (r_s, r_r, L_s, L_r) и по ним определяются постоянные времени Т_э и Т_r, лежащие в основе определения коэффициентов в регуляторах скорости и тока, и далее производится их корректировка с учетом тормозных моментов от продольного краевого эффекта. В соответствии с исследованиями, например [6], можно предположить, что в многополюсных ЛАД такой корректировки не понадобится. По-видимому, в дальнейшем встанет задача компенсации краевого эффекта на уровне систем управления. Причем компенсация возможна как на уровне вращающейся системы координат (x, y), так и в неподвижной системе a, b, c.

Условимся, что если преобразование из неподвижной системы статора (индуктора) с переменными a, b, c идет в направлении системы координат с переменными α, β и далее во вращающуюся систему с переменными x, y, то будем называть это прямым преобразованием, т.е.

a, b, c → α, β → x, y – прямое преобразование,

Тогда

x, y → α, β → a, b, c – обратное преобразование.

По данной схеме преобразования все сигналы с задатчика интенсивности (ЗИ), фильтров (ФЗТ, ФОТ), регуляторов (П, И) идут во вращающейся системе координат, а математическая модель линейного асинхронного двигателя (ЛАД) сделана в неподвижной системе координат (a, b, c), поэтому необходимо произвести двухэтапное преобразование сигналов.

Уровень 1. На этом уровне расположен задатчик интенсивности ЗИ. Он задает линейную синхронную скорость поля:

,

где τ – полюсное деление линейного асинхронного двигателя (рассмотрим двухполюсную машину);

f_c – частота питающего напряжения нарастающего по линейному закону до времени t_k, затем остающегося постоянным до конца времени переходного процесса.

% Программирование задатчика интенсивности Matlab-Script

dt=0.0005; tz=9.769*10^-3;

tau=3*tz; tk=5;

K=input('Длительность цикла k=');

for k=1:(K+1)

if ((k*dt >= 0) && (k*dt <= tk))

fc=k*dt*50/tk;

end;

if (k*dt > tk)

fc=50;

end;

vs=2*tau*fc;

mass_t(k)=k*dt;

mass_vs(k)=vs;

end;

% Построение графиков

figure(1);

plot(mass_t,mass_vs);

grid on;

Результат первого уровня приведен на рис. 2.

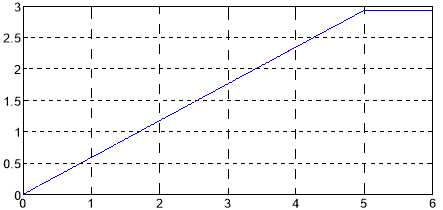
Рис. 2. Сигнал задатчика интенсивности

Уровень 2. Сигнал задания v_s поступает на регулятор скорости, на выходе которого получаем сигнал задания по проекции yi_{sy задания}. Регулятор скорости принимаем пропорциональным.

Уровень 3. Фильтры в цепи заданий и обратных связей по проекциям имеют одинаковую структуру, поэтому дадим общий вывод.

Пусть задана передаточная функция фильтра с постоянной T_μ в Simulink (рис. 3):

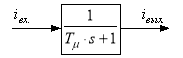
Рис. 3. Передаточная функция фильтра

Переведем это выражение в Script:

.

Перейдем от изображения к оригиналу:

;

.

Решаем дифференциальные уравнения методом конечных разностей Эйлера:

.

Конкретно к проекциям x и y:

;

.

Уровень 4. Пропорциональные и интегральные части регуляторов тока по проекциям одинаковы.

Пропорциональная часть K_Ix = K_Iy.

Интегральная часть:

 Проведем переход из Simulink в Script (рис. 4):

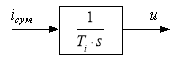
Рис. 4. Передаточная функция интегральной части регулятора тока

 Переходим к оригиналу:

 Выражаем через конечные разности:

;

;

;

;

;

;

;

;

.

Математическое моделирование u_x и u_y производится в Script. Результаты расчета даны на рис. 5.

% Программирование ux, uy в Matlab-Script

dt=0.0005; tz=9.769*10^-3; tau=3*tz;

tk=5; kc=6; Tm=0.005;

ixzad(1)=0; iyzad(1)=0; ixb=3;

Ki=1; Ti=0.48;

K=input('Длительность цикла k=');

for k=1:(K+1)

if ((k*dt >= 0) && (k*dt <= tk))

fc=k*dt*50/tk;

end;

if (k*dt > tk)

fc=50;

end;

vs=2*tau*fc;

vsum=vs;

iyb=vsum*kc;

ixzad(k+1)=ixzad(k)+(ixb-ixzad(k))*dt/Tm; %Фильтр ФЗТ x

iyzad(k+1)=iyzad(k)+(iyb-iyzad(k))*dt/Tm; %Фильтр ФЗТ y

ixsum(k+1)=ixzad(k+1);

iysum(k+1)=iyzad(k+1);

u1(k+1)=ixsum(k+1)*Ki; %Пропорциональная часть x

u2(k+1)=u2(k)+ixsum(k+1)*dt/Ti; %Интегральная часть x

ux=u1(k+1)+u2(k+1);

u3(k+1)=iysum(k+1)*Ki; %Пропорциональная часть y

u4(k+1)=u4(k)+iysum(k+1)*dt/Ti; %Интегральная часть y

uy=u3(k+1)+u4(k+1);

mass_t(k)=k*dt;

mass_ux(k)=ux;

mass_uy(k)=uy;

end;

% Построение графиков

figure(2);

plot(mass_t,mass_ux,'b',mass_t,mass_uy,'r');

grid on;

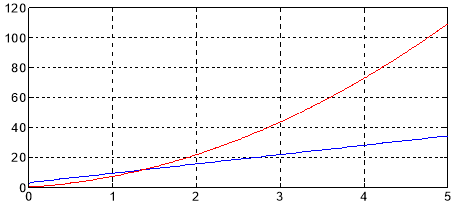
Рис. 5. Напряжения u_x, u_y на выходе регуляторов тока

Уровень 5. На этом уровне необходимо произвести математическое моделирование по обратному преобразованию из вращающейся системы x, y в неподвижную α, β. В соответствии с [3]:

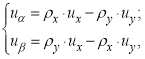
где определяется по следующим зависимостям:

- угловая скорость вращения системы координат;

- угол поворота.

В конечных разностях Эйлера:

или .

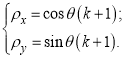
Так как главной задачей является изложение материала в понятной форме широкой аудитории студентов, математическое моделирование дадим с небольшой конечной частотой f_c = 1 Гц, при которой на рисунке (особенно в черно-белом изображении) были бы видны все графики переменных.

% Программирование ualfa, ubeta в Matlab-Script

dt=0.001; tz=9.769*10^-3; tau=3*tz; tk=8;

kc=6; Tm=0.005; ixzad(1)=0; iyzad(1)=0;

Ki=1; Ti=0.48; u2(1)=0; u4(1)=0;

ixb=3; teta(1)=0;

K=input('Длительность цикла k=');

for k=1:(K+1)

if ((k*dt >= 0) && (k*dt <= tk))

fc=k*dt*1/tk;

end;

if (k*dt > tk)

fc=1;

end;

vs=2*tau*fc;

vsum=vs;

iyb=vsum*kc;

wk=vs*pi/tau;

teta(k+1)=teta(k)+wk*dt;

ixzad(k+1)=ixzad(k)+(ixb-ixzad(k))*dt/Tm; %Фильтр ФЗТ x

iyzad(k+1)=iyzad(k)+(iyb-iyzad(k))*dt/Tm; %Фильтр ФЗТ y

ixsum(k+1)=ixzad(k+1);

iysum(k+1)=iyzad(k+1);

u1(k+1)=ixsum(k+1)*Ki; %Пропорциональная часть x

u2(k+1)=u2(k)+ixsum(k+1)*dt/Ti; %Интегральная часть x

ux=u1(k+1)+u2(k+1);

u3(k+1)=iysum(k+1)*Ki; %Пропорциональная часть y

u4(k+1)=u4(k)+iysum(k+1)*dt/Ti; %Интегральная часть y

uy=u3(k+1)+u4(k+1);

rox=cos(teta(k+1));

roy=sin(teta(k+1));

% 1 ступень обратного преобразования x,y -> alfa,beta

usalfa=rox*ux-roy*uy;

usbeta=roy*ux+rox*uy;

mass_t(k)=k*dt;

mass_usalfa(k)=usalfa;

mass_usbeta(k)=usbeta;

end;

% Построение графиков

figure(3);

plot(mass_t,mass_usalfa,'b',mass_t,mass_usbeta,'r');

grid on;

Результаты пятого уровня представлены на рис. 6.

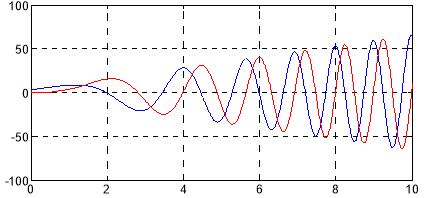
Рис. 6. Напряжения u_α, u_β на выходе регуляторов тока

Уровень 6. На этом уровне необходимо преобразовать сигналы u_α, u_β в трехфазную систему U_a, U_b и U_c, непосредственно подаваемых в математическую модель АИН ШИМ.

Уравнения преобразования, в соответствии с [3], имеют следующий вид:

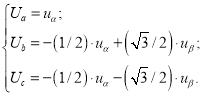
% Программирование Ua, Ub, Uc в Matlab-Script

dt=0.001; tz=9.769*10^-3; tau=3*tz; tk=8;

kc=6; Tm=0.005; ixzad(1)=0; iyzad(1)=0;

Ki=1; Ti=0.48; u2(1)=0; u4(1)=0;

ixb=3; teta(1)=0;

K=input('Длительность цикла k=');

for k=1:(K+1)

if ((k*dt >= 0) && (k*dt <= tk))

fc=k*dt*1/tk;

end;

if (k*dt > tk)

fc=1;

end;

vs=2*tau*fc;

vsum=vs;

iyb=vsum*kc;

wk=vs*pi/tau;

teta(k+1)=teta(k)+wk*dt;

ixzad(k+1)=ixzad(k)+(ixb-ixzad(k))*dt/Tm; %Фильтр ФЗТ x

iyzad(k+1)=iyzad(k)+(iyb-iyzad(k))*dt/Tm; %Фильтр ФЗТ y

ixsum(k+1)=ixzad(k+1);

iysum(k+1)=iyzad(k+1);

u1(k+1)=ixsum(k+1)*Ki; %Пропорциональная часть x

u2(k+1)=u2(k)+ixsum(k+1)*dt/Ti; %Интегральная часть x

ux=u1(k+1)+u2(k+1);

u3(k+1)=iysum(k+1)*Ki; %Пропорциональная часть y

u4(k+1)=u4(k)+iysum(k+1)*dt/Ti; %Интегральная часть y

uy=u3(k+1)+u4(k+1);

rox=cos(teta(k+1));

roy=sin(teta(k+1));

% 1 ступень обратного преобразования x,y -> alfa,beta

usalfa=rox*ux-roy*uy;

usbeta=roy*ux+rox*uy;

% 2 ступень обратного преобразования alfa,beta -> a,b,c

Ua=usalfa;

Ub=-(1/2)*usalfa+(sqrt(3)/2)*usbeta;

Uc=-(1/2)*usalfa-(sqrt(3)/2)*usbeta;

mass_t(k)=k*dt;

mass_Ua(k)=Ua;

mass_Ub(k)=Ub;

mass_Uc(k)=Uc;

end;

% Построение графиков

figure(4);

plot(mass_t,mass_Ua,'b',mass_t,mass_Ub,'r',mass_t,mass_Uc,'g');

grid on;

Результаты шестого уровня представлены на рис. 7.

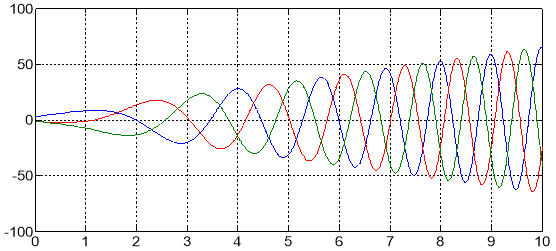
Рис. 7. Напряжения U_a, U_b, U_c

Уровень 7. Математическая модель инвертора напряжения с широтно-импульсной модуляцией в Script приведена ниже.

% Программирование Uashim, Ubshim, Ucshim в Matlab-Script

dt=0.00001; tz=9.769*10^-3; tau=3*tz; tk=8; kc=6;

Tm=0.005; ixzad(1)=0; iyzad(1)=0; Ki=1; Ti=0.48;

u2(1)=0; u4(1)=0; ixb=3; teta(1)=0; kinv=380;

tau1=0; time=0; u0p(1)=1; pwm=-1; f_triangle=1000;

K=input('Длительность цикла k=');

for k=1:(K+1)

if ((k*dt >= 0) && (k*dt <= tk))

fc=k*dt*1/tk;

end;

if (k*dt > tk)

fc=1;

end;

vs=2*tau*fc;

vsum=vs;

iyb=vsum*kc;

wk=vs*pi/tau;

teta(k+1)=teta(k)+wk*dt;

ixzad(k+1)=ixzad(k)+(ixb-ixzad(k))*dt/Tm; %Фильтр ФЗТ x

iyzad(k+1)=iyzad(k)+(iyb-iyzad(k))*dt/Tm; %Фильтр ФЗТ y

ixsum(k+1)=ixzad(k+1);

iysum(k+1)=iyzad(k+1);

u1(k+1)=ixsum(k+1)*Ki; %Пропорциональная часть x

u2(k+1)=u2(k)+ixsum(k+1)*dt/Ti; %Интегральная часть x

ux=u1(k+1)+u2(k+1);

u3(k+1)=iysum(k+1)*Ki; %Пропорциональная часть y

u4(k+1)=u4(k)+iysum(k+1)*dt/Ti; %Интегральная часть y

uy=u3(k+1)+u4(k+1);

rox=cos(teta(k+1));

roy=sin(teta(k+1));

% 1 ступень обратного преобразования x,y -> alfa,beta

usalfa=rox*ux-roy*uy;

usbeta=roy*ux+rox*uy;

% 2 ступень обратного преобразования alfa,beta -> a,b,c

Ua(k+1)=usalfa;

Ub(k+1)=-(1/2)*usalfa+(sqrt(3)/2)*usbeta;

Uc(k+1)=-(1/2)*usalfa-(sqrt(3)/2)*usbeta;

% Система АИН ШИМ

if ((k*dt >= 0) && (k*dt <= 0.1))

U0=k*dt*abs(sqrt((usalfa^2)+(usbeta^2)))/0.1;

end;

if (k*dt > 0.1)

U0=abs(sqrt((usalfa^2)+(usbeta^2)));

end;

tau1(k+1)=tau1(k)+dt*f_triangle;

time(k+1)=time(k)+dt;

if tau1(k+1)>=1

tau1(k+1)=tau1(k+1)-1;

end;

if (tau1(k+1)>=0) && (tau1(k+1)<0.5)

f1(k)=1-4*tau1(k+1);

else

f1(k)=4*tau1(k+1)-3;

end;

u0p(k+1)=U0*f1(k);

if (Ua(k+1)>=u0p(k+1))

pwm(k+1)=1;

else

pwm(k+1)=-1;

end;

if (Ub(k+1)>=u0p(k+1))

pwm_2pi3(k+1)=1;

else

pwm_2pi3(k+1)=-1;

end;

if (Uc(k+1)>=u0p(k+1))

pwm_4pi3(k+1)=1;

else

pwm_4pi3(k+1)=-1;

end;

Uashim(k+1)=kinv*(1/2)*((2*(pwm(k+1)))/3-(pwm_2pi3(k+1))/3-(pwm_4pi3(k+1))/3);

Ubshim(k+1)=kinv*(1/2)*(-pwm(k+1)/3+(2*pwm_2pi3(k+1))/3-pwm_4pi3(k+1)/3);

Ucshim(k+1)=kinv*(1/2)*(-pwm(k+1)/3-pwm_2pi3(k+1)/3+(2*pwm_4pi3(k+1))/3);

mass_t(k)=k*dt;

mass_u0p(k)=u0p(k+1);

end;

% Построение графиков

figure(5);

plot(mass_t,mass_u0p,'b');

grid on;

На рис. 8 показан результат расчета опорного напряжения u_оп с частотой f_triangle = 1000 и изменяющейся амплитудой.

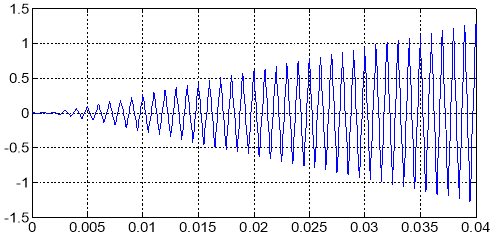
Рис. 8. Опорное напряжение u_оп, с которым сравниваются напряжения U_a, U_b, U_c на выходе преобразователя координат (α, β → a, b, c)

Остальные уровни в разомкнутой системе проводятся аналогично статье [2].

Наконец, приступим к главной части – замыканию всех обратных связей.

Математическое моделирование САР скорости системы «АИН ШИМ – ЛАД».

САР скорости системы «АИН ШИМ – ЛАД» показана на рис. 9.

% Математическая модель САР скорости системы АИН ШИМ - ЛАД с укладкой статорной обмотки классическим способом (z=6) с нулевым проводом

% Исходные данные асинхронного двигателя

Rb=0.1003*10^7; rs=9.5; LsA=0.037; LsB=0.038; LsC=0.035; rr=4.6345*10^-5; Lr=0.0372*10^-5; dt=0.00001; As=rs+LsA/dt; Bs=rs+LsB/dt;

Cs=rs+LsC/dt; tz=9.769*10^-3; tau=3*tz; m=15.2; v0=0; wn=200; UA=wn/dt; F=0; tk=0.5; kc=40;

Tm=0.005; ixzad(1)=0; iyzad(1)=0; ix(1)=0; iy(1)=0; Ki=10; Ti=0.24; u4(1)=0; ixb=5; u2(1)=0;

teta(1)=0; Fc=40; um=0.5; kinv=380; tau1=0; time=0; u0p(1)=1; pwm=-1; f_triangle=1000;

X=zeros(18,1);

K=input('Длительность цикла k=');

for k=1:(K+1)

if ((k*dt >= 0) && (k*dt <= tk))

fc=k*dt*40/tk;

end;

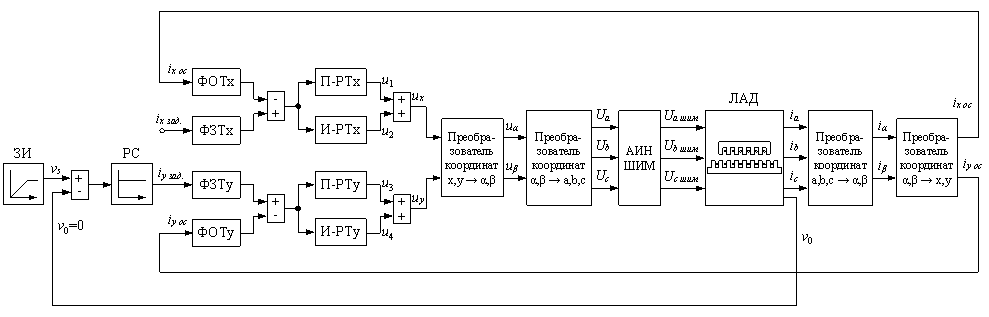Рис. 9. САР скорости системы «АИН ШИМ – ЛАД»

if (k*dt > tk)

fc=40;

end;

v(1,k)=v0; % Создание вектор-строки для графика скорости

f(1,k)=sum(F); % Создание вектор-строки для графика усилия

i0(1,k)=X(18);

i_a(1,k)=X(15);

i_b(1,k)=X(17);

i_c(1,k)=X(16);

vs=2*tau*fc;

vsum=vs-v0;

iyb=vsum*kc;

wk=vs*pi/tau;

teta(k+1)=teta(k)+wk*dt;

rox=cos(teta(k+1));

roy=sin(teta(k+1));

% 1 ступень прямого преобразования a,b,c -> alfa,beta

i_alfa=(1/3)*(2*i_a(1,k)-i_b(1,k)-i_c(1,k));

i_beta=(1/sqrt(3))*(i_b(1,k)-i_c(1,k));

% 2 ступень прямого преобразования alfa,beta -> x,y

ixoc(k)=rox*i_alfa+roy*i_beta;

iyoc(k)=-roy*i_alfa+rox*i_beta;

ixoc1(k+1)=ixoc(k)+(ix-ixoc(k))*dt/Tm; %Фильтр ФОТ x

ixzad(k+1)=ixzad(k)+(ixb-ixzad(k))*dt/Tm; %Фильтр ФЗТ x

iyoc1(k+1)=iyoc(k)+(iy-iyoc(k))*dt/Tm; %Фильтр ФОТ y

iyzad(k+1)=iyzad(k)+(iyb-iyzad(k))*dt/Tm; %Фильтр ФЗТ y

ixsum(k+1)=ixzad(k+1)-ixoc1(k+1);

iysum(k+1)=iyzad(k+1)-iyoc1(k+1);

u1(k+1)=ixsum(k+1)*Ki; %Пропорциональная часть x

u2(k+1)=u2(k)+ixsum(k+1)*dt/Ti; %Интегральная часть x

ux=u1(k+1)+u2(k+1);

u3(k+1)=iysum(k+1)*Ki; %Пропорциональная часть y

u4(k+1)=u4(k)+iysum(k+1)*dt/Ti; %Интегральная часть y

uy=u3(k+1)+u4(k+1);

% 1 ступень обратного преобразования x,y -> alfa,beta

usalfa=rox*ux-roy*uy;

usbeta=roy*ux+rox*uy;

% 2 ступень обратного преобразования alfa,beta -> a,b,c

Ua(k+1)=usalfa;

Ub(k+1)=-(1/2)*usalfa+(sqrt(3)/2)*usbeta;

Uc(k+1)=-(1/2)*usalfa-(sqrt(3)/2)*usbeta;

% Система АИН ШИМ

if ((k*dt >= 0) && (k*dt <= 0.1))

U0=k*dt*abs(sqrt((usalfa^2)+(usbeta^2)))/0.1;

end;

if (k*dt > 0.1)

U0=abs(sqrt((usalfa^2)+(usbeta^2)));

end;

tau1(k+1)=tau1(k)+dt*f_triangle;

time(k+1)=time(k)+dt;

if tau1(k+1)>=1

tau1(k+1)=tau1(k+1)-1;

end;

if (tau1(k+1)>=0) && (tau1(k+1)<0.5)

f1(k)=1-4*tau1(k+1);

else

f1(k)=4*tau1(k+1)-3;

end;

u0p(k+1)=U0*f1(k);

if (Ua(k+1)>=u0p(k+1))

pwm(k+1)=1;

else

pwm(k+1)=-1;

end;

if (Ub(k+1)>=u0p(k+1))

pwm_2pi3(k+1)=1;

else

pwm_2pi3(k+1)=-1;

end;

if (Uc(k+1)>=u0p(k+1))

pwm_4pi3(k+1)=1;

else

pwm_4pi3(k+1)=-1;

end;

Uashim(k+1)=kinv*(1/2)*((2*(pwm(k+1)))/3-(pwm_2pi3(k+1))/3-(pwm_4pi3(k+1))/3);

Ubshim(k+1)=kinv*(1/2)*(-pwm(k+1)/3+(2*pwm_2pi3(k+1))/3-pwm_4pi3(k+1)/3);

Ucshim(k+1)=kinv*(1/2)*(-pwm(k+1)/3-pwm_2pi3(k+1)/3+(2*pwm_4pi3(k+1))/3);

% Формирование матрицы А

A=zeros(18);

B=2*Rb*(rr+Lr/dt)+1/dt;

B1=6*Rb*(rr+Lr/dt)+(-4*Rb)*Lr*v0/(2*tz)+1/dt;

B2=55*Rb*(rr+Lr/dt)+(-45*Rb)*Lr*v0/(2*tz)+1/dt;

B3=550*Rb*(rr+Lr/dt)+(-450*Rb)*Lr*v0/(2*tz)+1/dt;

B4=1000*Rb*(rr+Lr/dt)+1/dt;

B5=550*Rb*(rr+Lr/dt)+450*Rb*Lr*v0/(2*tz)+1/dt;

B6=55*Rb*(rr+Lr/dt)+(45*Rb)*Lr*v0/(2*tz)+1/dt;

B7=6*Rb*(rr+Lr/dt)+(4*Rb)*Lr*v0/(2*tz)+1/dt;

C=-Rb*(rr+Lr/dt)+(2*Rb*Lr+1)*v0/(2*tz);

C1=-Rb*(rr+Lr/dt)+(6*Rb*Lr+1)*v0/(2*tz);

C2=-5*Rb*(rr+Lr/dt)+(55*Rb*Lr+1)*v0/(2*tz);

C3=-50*Rb*(rr+Lr/dt)+(550*Rb*Lr+1)*v0/(2*tz);

C4=-500*Rb*(rr+Lr/dt)+(1000*Rb*Lr+1)*v0/(2*tz);

C5=-500*Rb*(rr+Lr/dt)+(550*Rb*Lr+1)*v0/(2*tz);

C6=-50*Rb*(rr+Lr/dt)+(55*Rb*Lr+1)*v0/(2*tz);

C7=-5*Rb*(rr+Lr/dt)+(6*Rb*Lr+1)*v0/(2*tz);

D=-Rb*Lr*v0/(2*tz);

D1=5*D;D2=50*D;D3=500*D;

E=-Rb*(rr+Lr/dt)-(2*Rb*Lr+1)*v0/(2*tz);

E1=-5*Rb*(rr+Lr/dt)-(6*Rb*Lr+1)*v0/(2*tz);

E2=-50*Rb*(rr+Lr/dt)-(55*Rb*Lr+1)*v0/(2*tz);

E3=-500*Rb*(rr+Lr/dt)-(550*Rb*Lr+1)*v0/(2*tz);

E4=-500*Rb*(rr+Lr/dt)-(1000*Rb*Lr+1)*v0/(2*tz);

E5=-50*Rb*(rr+Lr/dt)-(550*Rb*Lr+1)*v0/(2*tz);

E6=-5*Rb*(rr+Lr/dt)-(55*Rb*Lr+1)*v0/(2*tz);

E7=-Rb*(rr+Lr/dt)-(6*Rb*Lr+1)*v0/(2*tz);

T=-wn*Lr*v0/(2*tz);

Y=-wn*(rr+Lr/dt);

W1=-wn*Lr/dt;

P=-Rb*Lr/dt;

Q=(2*Rb*Lr+1)/dt;

Q1=(6*Rb*Lr+1)/dt;

Q2=(55*Rb*Lr+1)/dt;

Q3=(550*Rb*Lr+1)/dt;

Q4=(1000*Rb*Lr+1)/dt;

for n=1:3

A(n+3,n+14)=(-1)^(n+1)*T;

A(n+4,n+14)=(-1)^(n+1)*Y;

A(n+5,n+14)=(-1)^n*T;

A(n+6,n+14)=(-1)^n*T;

A(n+7,n+14)=(-1)^n*Y;

A(n+8,n+14)=(-1)^(n+1)*T;

end;

for n=1:3

A(18,n+14)=1;

end;

A(18,18)=-1;

for n=1:6

A(n+4,n+4)=B;

A(n+5,n+4)=E;

A(n+3,n+4)=C;

end;

for n=1:7

A(n+2,n+4)=D;

A(n+5,n+3)=-D;

end;

A(1,1)=B4; A(1,2)=C5; A(1,3)=D2; A(2,1)=E4; A(2,2)=B5; A(2,3)=C6; A(2,4)=D1; A(3,1)=-D3; A(3,2)=E5; A(3,3)=B6;

A(3,4)=C7; A(4,2)=-D2; A(4,3)=E6; A(4,4)=B7; A(5,3)=-D1; A(5,4)=E7; A(10,11)=C1; A(10,12)=D1; A(11,11)=B1; A(11,12)=C2;

A(11,13)=D2; A(12,11)=E1; A(12,12)=B2; A(12,13)=C3; A(12,13)=D3; A(13,11)=-D1; A(13,12)=E2; A(13,13)=B3; A(13,14)=C4; A(14,12)=-D2;

A(14,13)=E3; A(14,14)=B4; A(15,5)=UA; A(16,7)=UA; A(17,9)=UA; A(15,8)=-UA; A(16,10)=-UA; A(17,6)=-UA; A(15,15)=As; A(16,17)=Bs; A(17,16)=Cs;

% Матрица свободных членов

S=[ Q4*X(1)+P*( 500*X(2)); %1

Q3*X(2)+P*(500*X(1)+50*X(3)); %2

Q2*X(3)+P*(50*X(2)+5*X(4)); %3

Q1*X(4)+P*(5*X(3)+X(5)); %4

W1*X(15)+Q*X(5)+P*(X(4)+X(6)); %5

(-1)*W1*X(16)+Q*X(6)+P*(X(5)+X(7)); %6

W1*X(17)+Q*X(7)+P*(X(6)+X(8)); %7

(-1)*W1*X(15)+Q*X(8)+P*(X(7)+X(9)); %8

W1*X(16)+Q*X(9)+P*(X(8)+X(10)); %9

(-1)*W1*X(17)+Q*X(10)+P*(X(9)+X(11)); %10

Q1*X(11)+P*(X(10)+5*X(12)); %11

Q2*X(12)+P*(5*X(11)+50*X(13)); %12

Q3*X(13)+P*(50*X(12)+500*X(14)); %13

Q4*X(14)+P*500*X(13); %14

UA*(X(5)-X(8))+(LsA/dt)*X(15)+Uashim(k+1); %15

UA*(X(7)-X(10))+(LsB/dt)*X(17)+Ubshim(k+1); %16

UA*(X(9)-X(6))+(LsC/dt)*X(16)+Ucshim(k+1); %17

0]; %18

% Решение методом Гаусса-Жордана

Z=rref([A S]); %Приведение расширенной матрицы к треугольному виду

X=Z(1:18,19:19); %Выделение последнего столбца из матрицы

% Ток в роторе

Ir=[ 1000*Rb*X(1)-Rb*(500*X(2)); %1

550*Rb*X(2)-Rb*(500*X(1)+50*X(3)); %2

55*Rb*X(3)-Rb*(50*X(2)+5*X(4)); %3

6*Rb*X(4)-Rb*(5*X(3)+X(5)); %4

-wn*X(15)+2*Rb*X(5)-Rb*(X(4)+X(6)); %5

(-1)*(-wn)*X(16)+2*Rb*X(6)-Rb*(X(5)+X(7)); %6

-wn*X(17)+2*Rb*X(7)-Rb*(X(6)+X(8)); %7

(-1)*(-wn)*X(15)+2*Rb*X(8)-Rb*(X(7)+X(9)); %8

-wn*X(16)+2*Rb*X(9)-Rb*(X(8)+X(10)); %9

(-1)*(-wn)*X(17)+2*Rb*X(10)-Rb*(X(9)+X(11)); %10

6*Rb*X(11)-Rb*(X(10)+5*X(12)); %11

55*Rb*X(12)-Rb*(5*X(11)+50*X(13)); %12

550*Rb*X(13)-Rb*(50*X(12)+500*X(14)); %13

1000*Rb*X(14)-Rb*(500*X(13))]; %14

% Электромагнитное усилие

F(1)=X(2)*Ir(1)/(2*tz);

for n=1:12

F(n+1)=(X(n+2)-X(n))*Ir(n+1)/(2*tz);

end;

F(14)=-X(13)*Ir(14)/(2*tz);

% Скорость

v0=v0+((sum(F)-Fc)/m)*dt;

mass_t(k)=k*dt;

mass_vs(k)=vs;

mass_v0(k)=v0;

mass_ixb(k)=ixb;

mass_iyb(k)=iyb;

mass_ixoc(k)=ixoc(k);

mass_iyoc(k)=iyoc(k);

mass_i_a(k)=i_a(1,k);

mass_i_b(k)=i_b(1,k);

mass_i_c(k)=i_c(1,k);

mass_i_alfa(k)=i_alfa;

mass_i_beta(k)=i_beta;

% Построение графиков

figure(1);

plot(mass_t,mass_vs,'b',mass_t,mass_v0,'r');

grid on;

figure(2);

plot(mass_t,mass_ixb,'b',mass_t,mass_ixoc,'r');

grid on;

figure(3);

plot(mass_t,mass_iyb,'b',mass_t,mass_iyoc,'r');

grid on;

figure(4);

plot(mass_t,mass_i_a,'b',mass_t,mass_i_b,'r',mass_t,mass_i_c,'g');

grid on;

figure(5);

plot(mass_t,mass_i_alfa,'b',mass_t,mass_i_beta,'r');

grid on;

figure(6);

plot(mass_t,mass_ixoc,'b',mass_t,mass_iyoc,'r');

grid on;

figure(7);

k=0:K;

subplot(2,1,1);

plot(k*dt,v);

title('Линейная скорость');

xlabel('t,c');

ylabel('v,m/c');

grid on;

subplot(2,1,2);

plot(k*dt,f);

title('Электромагнитное усилие');

xlabel('t,c');

ylabel('F,H');

grid on;

Результаты расчетов приведены на рис. 10, …, 16.

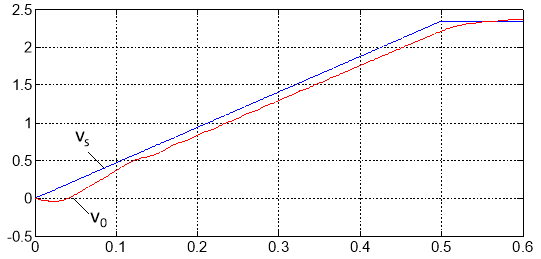
Рис. 10. Задание на скорость v_s и скорость v₀ ЛАД

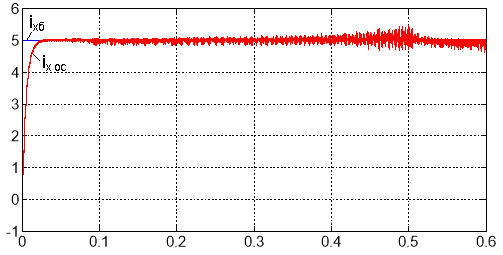
Рис. 11. Токи i_xб и i_{x oc} на входе фильтров ФЗТ и ФОТ

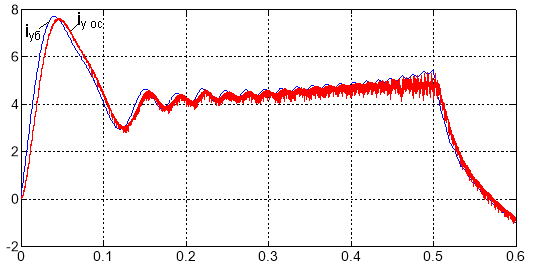
Рис. 12. Токи i_yб и i_{y oc} на входе фильтров ФЗТ и ФОТ

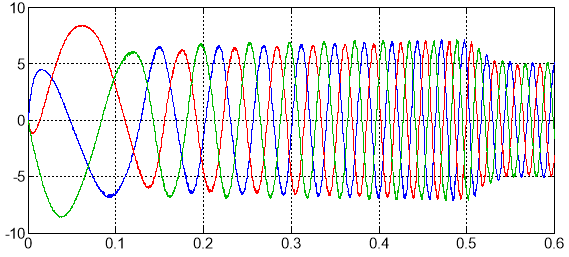
Рис. 13. Токи i_а, i_b, i_c на выходе ЛАД

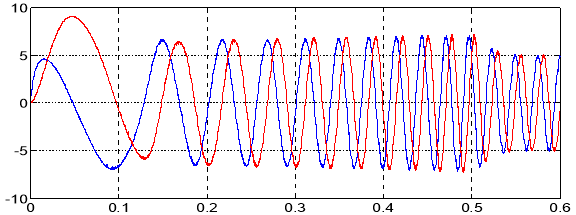
Рис. 14. Токи i_α, i_β на выходе преобразователя (a, b, c → α, β)

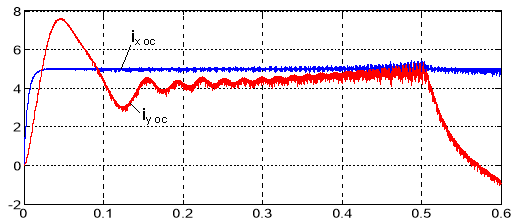
Рис. 15. Токи i_{x ос}, i_{y ос} на выходе прямого преобразователя координат

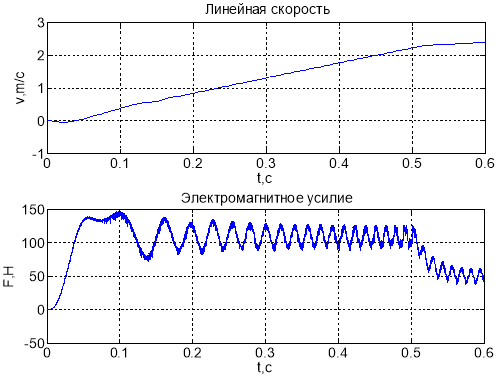
Рис. 16. График скорости и момента в замкнутой системе

Литература:

1. Сарапулов Ф.Н., Емельянов А.А., Иваницкий С.В., Резин М.Г. Исследование электромеханических переходных процессов линейного асинхронного короткозамкнутого двигателя // Электричество. - 1982. – №10. – С. 54–57.
2. Емельянов А.А., Бесклеткин В.В., Прокопьев К.В., Ситенков А.А., Бурхацкий В.В., Мальцев Н.В. Математическая модель САР скорости линейного асинхронного двигателя на магнитных схемах замещения// Молодой ученый. – 2016. – №4. – С. 113-135.
3. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург УРО РАН, 2000. - 654 с.
4. Шрейнер Р.Т., Емельянов А.А., Медведев А.В. Оптимизация перемежающихся режимов работы частотно-регулируемого асинхронного электропривода // Известия ТулГУ. Технические науки. Вып. 3: в 5 ч. Туда: Изд-во ТулГУ, 2010. Ч 4. - 262 с.
5. Шрейнер Р.Т., Емельянов А.А., Медведев А.В. Ресурсы энергосбережения в повторно-кратковременных режимах работы асинхронного привода // Промышленная энергетика. - 2011. - №11. - С. 22-27.
6. Веселовский О.Н., Коняев А.Ю., Сарапулов Ф.Н. Линейные асинхронные двигатели. - М.: – Энергоатомиздат, 1991. – 256 с.

1