Математическое моделирование системы «АИН ШИМ – АД» с транзисторными ключами
Емельянов Александр Александрович, доцент;
Бесклеткин Виктор Викторович, ассистент;
Прокопьев Константин Васильевич, студент;
Ситенков Александр Александрович, студент;
Бурхацкий Владимир Владимирович, студент;
Мальцев Никита Васильевич, студент;
Авдеев Александр Сергеевич, студент;
Габзалилов Эльвир Фиргатович, студент
Российский государственный профессионально-педагогический университет
В отличие от работы [1] в системе «АИН ШИМ – АД» смоделированы идеализированные транзисторные ключи в инверторе без учета «мертвого времени» их переключения [2], [3]. На рис. 1 приведена полная схема разомкнутой системы при прямом пуске.
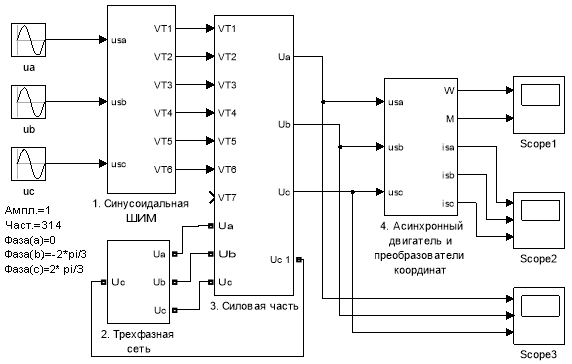
Рис. 1. Полная схема системы «АИН ШИМ – АД»
В этой схеме под каждым элементом дана нумерация, а именно:
- Синусоидальная ШИМ (рис. 2).
- Трехфазная сеть (рис. 3).
- Силовая часть (рис. 4).
- Асинхронный двигатель и преобразователи координат (рис. 5).
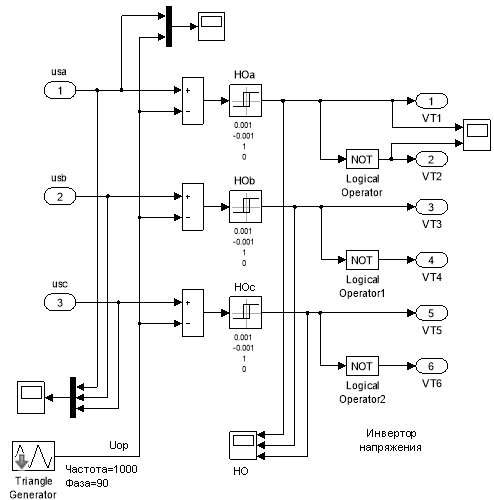
Рис. 2. Блок «Синусоидальная ШИМ»
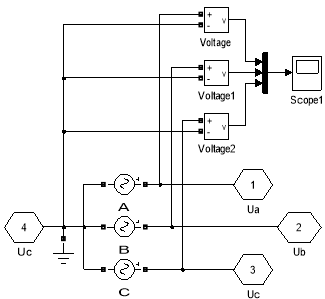
Рис. 3. Трехфазная сеть
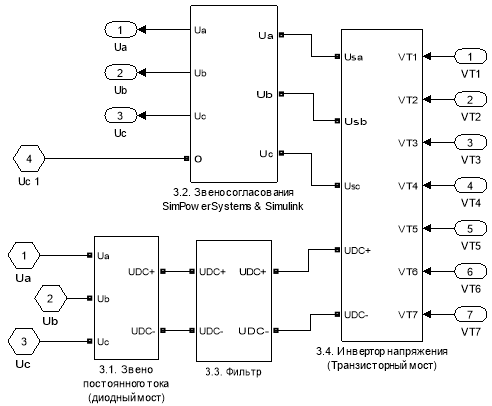
Рис. 4. Силовая часть
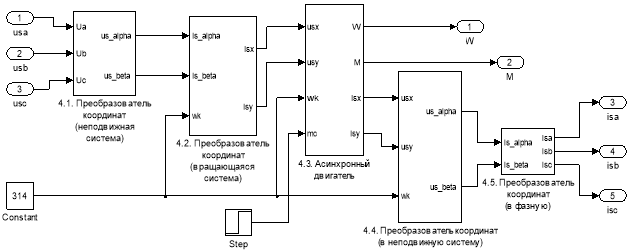
Рис. 5. Асинхронный двигатель и преобразователи координат
Элемент 3 (силовая часть) состоит из следующих субблоков:
3.1. Звено постоянного тока (диодный мост) (рис. 6).
3.2. Звено согласования SimPowerSystems & Simulink (рис. 7).
3.3. Фильтр (рис. 8).
3.4. Инвертор напряжения (транзисторный мост) (рис. 9).
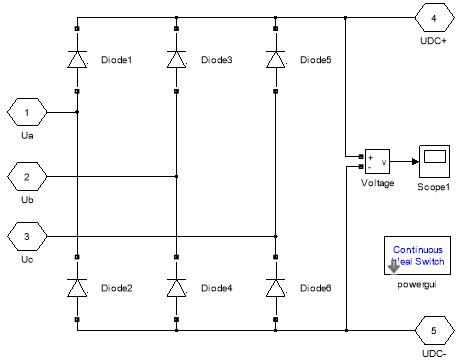
Рис. 6. Звено постоянного тока (диодный мост)
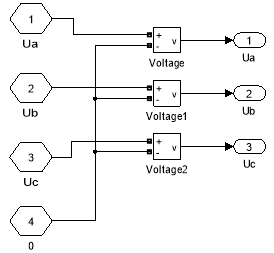
Рис. 7. Звено согласования SimPowerSystems & Simulink
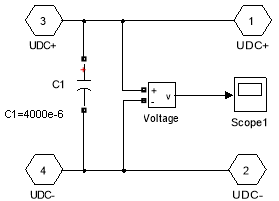
Рис. 8. Фильтр
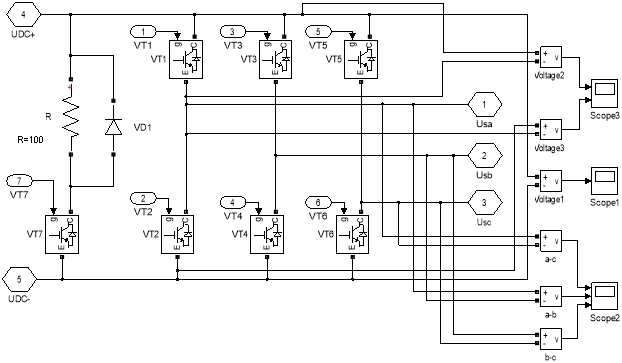
Рис. 9. Инвертор напряжения (транзисторный мост)
Элемент 4 (асинхронный двигатель и преобразователи координат) содержит субблоки:
4.1. Преобразователь координат из трехфазной системы в неподвижную (рис. 10).
4.2. Преобразователь координат из неподвижной системы во вращающуюся (рис. 11).
4.3. Модель асинхронного двигателя (рис. 14).
4.4. Обратное преобразование из вращающейся системы координат в неподвижную (рис. 12).
4.5. Преобразователь координат из неподвижной системы в трехфазную (рис. 13).
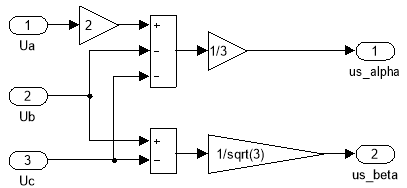
Рис. 10. Преобразователь координат из трехфазной системы в неподвижную
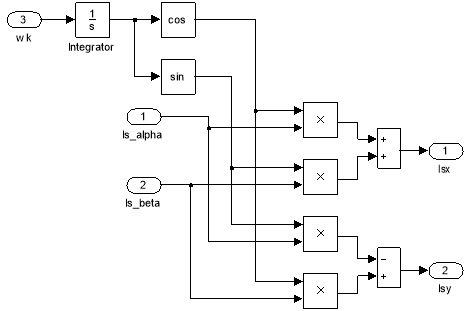
Рис. 11. Преобразователь координат из неподвижной системы во вращающуюся
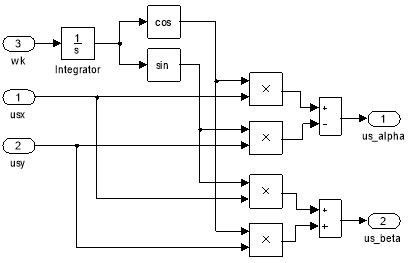
Рис. 12. Обратное преобразование из вращающейся системы координат в неподвижную
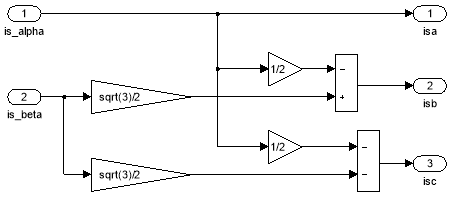
Рис. 13. Преобразователь координат из неподвижной системы в трехфазную
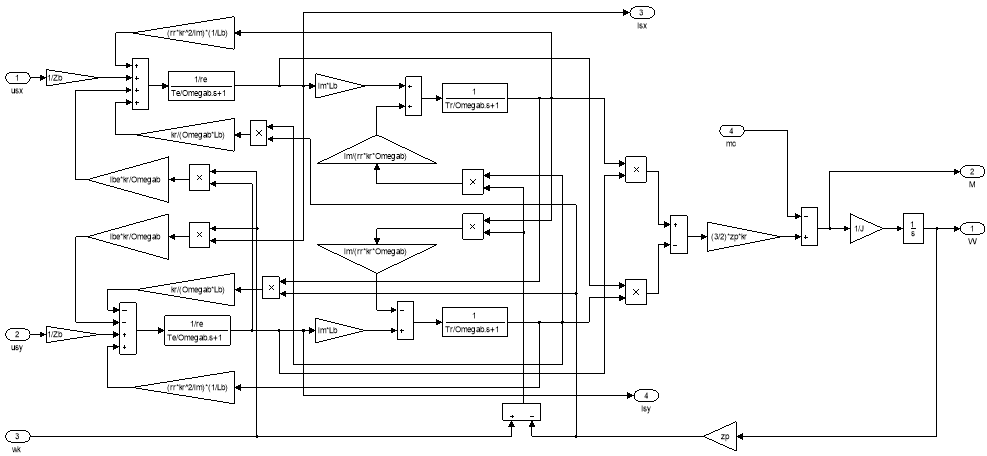
Рис. 14. Модель асинхронного двигателя
Результаты математического моделирования приведены на рис. 15, …, 19.
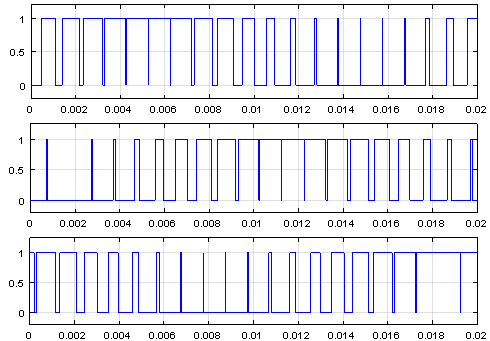
Рис. 15. Сигналы на выходе нуль-органов
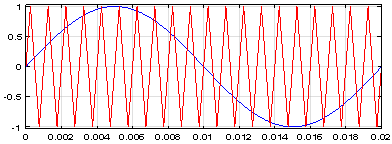
Рис. 16. Сравнение сигналов опорного напряжения с сигналом задания
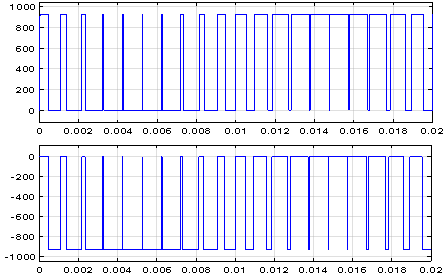
Рис. 17. Сравнение напряжений в стойке фазы «А» на Scope3 в блоке инвертора напряжения
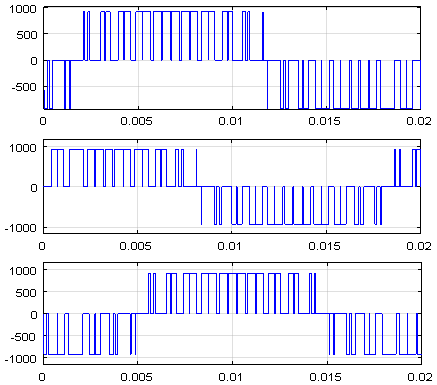
Рис. 18. Линейные напряжения на нагрузке
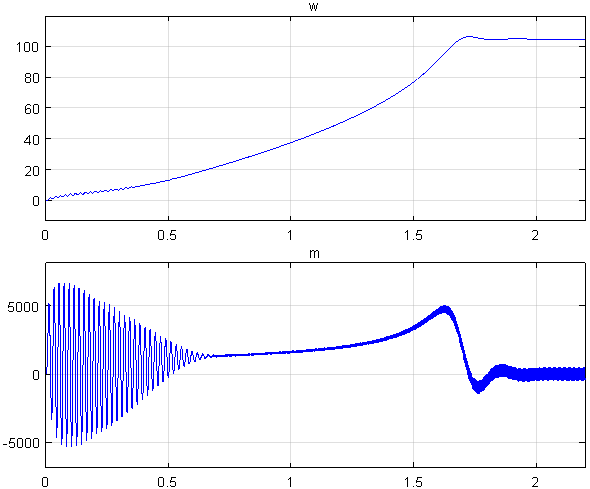
Рис. 19. Графики скорости и момента
Литература:
- Емельянов А. А., Бесклеткин В. В., Авдеев А. С., Чернов М. В., Киряков Г. А., Габзалилов Э. Ф. Моделирование САР скорости асинхронного двигателя с переменными ψr-is на основе апериодических звеньев в Script-Simulink // Молодой ученый. – 2015. – №23. – С. 24-34.
- Шрейнер Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин. Под ред. проф. д. т. н. Р. Т. Шрейнера. – Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. – 361 с.
- Шрейнер Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. – 654 с.

