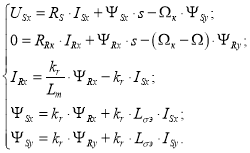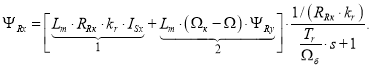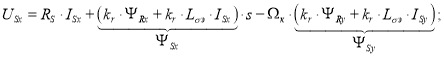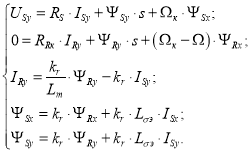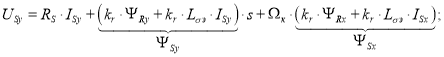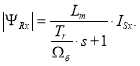Моделирование САР скорости системы «АИН ШИМ – АД» с переменными ΨR - IS сконтуром потока в системе абсолютных единиц
Емельянов Александр Александрович, старший преподаватель;
Бесклеткин Виктор Викторович, старший преподаватель;
Гусев Владимир Михайлович, студент магистратуры;
Маклыгин Константин Андреевич, студент;
Коновалов Илья Дмитриевич, студент;
Камеристов Кирилл Владимирович, студент
Российский государственный профессионально-педагогический университет (г. Екатеринбург)
Пестеров Дмитрий Ильич, студент магистратуры
Уральский государственный университет путей сообщения (г. Екатеринбург)
В этой статье рассмотрена САР скорости АД с контуром потока и синусоидальной ШИМ в системе абсолютных единиц, являющаяся дальнейшим развитием работы [1].
В работе [1] были получены уравнения асинхронного двигателя по проекции x (+1):
|
|
(1) |
|
(2) | |
|
(3) | |
|
(4) | |
|
(5) |
Подставим уравнение (3) в (2):
![]()
Отсюда выразим слагаемое ![]() :
:
|
|
(6) |
Для получения апериодического звена перенесем слагаемые с ΨRx в левую часть и умножим обе части уравнения на Lm:
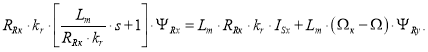
Обозначим постоянную времени потока в реальном времени ![]() :
:
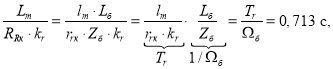
где ![]() - постоянная времени потока в машинном (ЭВМ) времени
- постоянная времени потока в машинном (ЭВМ) времени ![]() .
.
Составляющая потокосцепления ротора ΨRx определится в следующей форме:
|
|
(7) |
Структурная схема для определения потокосцепления ΨRx приведена на рис. 1.
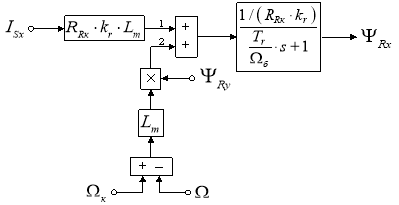
Рис. 1. Структурная схема для определения потокосцепления ΨRx
Подставим выражения ΨSx и ΨSy из уравнений (4) и (5) в уравнение (1):
|
|
(8) |
![]()
В полученное уравнение подставим выражение (6) и перенесем слагаемые с переменными ISx в левую часть:
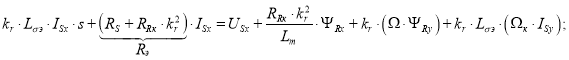
![]()
Обозначим постоянную времени статорной обмотки в реальном времени ![]() :
:
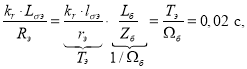
где ![]() - постоянная времени статорной обмотки в машинном (ЭВМ) времени
- постоянная времени статорной обмотки в машинном (ЭВМ) времени ![]() .
.
Составляющая статорного тока ISx определится в следующей форме:
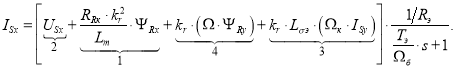
Структурная схема для определения тока ISx дана на рис. 2.
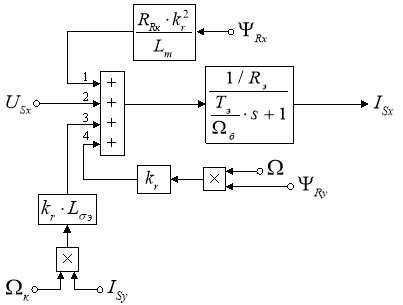
Рис. 2. Структурная схема для определения тока ISx
Аналогично, выразим ΨRy и ISy из системы уравнений по проекции y (+j):
|
|
(9) |
|
(10) | |
|
(11) | |
|
(12) | |
|
(13) |
Подставим уравнение (11) в (10) и выразим ![]() :
:
![]()
|
|
(14) |
Перенесем слагаемые с ΨRy в левую часть и умножим обе части уравнения на Lm:
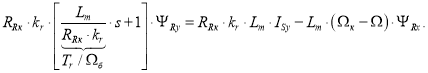
Потокосцепление ΨRy определится в следующей форме:
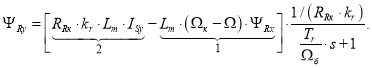
Структурная схема для определения потокосцепления ΨRy приведена на рис. 3.
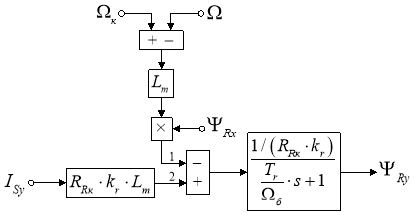
Рис. 3. Структурная схема для определения потокосцепления ΨRy
Для определения ISy подставим уравнения (12) и (13) в (9):
|
|
(15) |
![]()
В полученное уравнение подставим ![]() из (14) и перенесем слагаемые с переменными ISy в левую часть:
из (14) и перенесем слагаемые с переменными ISy в левую часть:
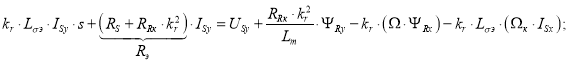
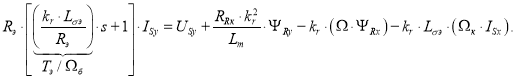
Ток ISy определится в следующей форме:
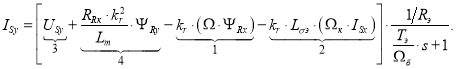
Структурная схема для определения ISy приведена на рис. 4.
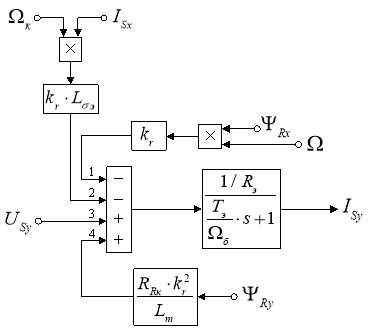
Рис. 4. Структурная схема для определения тока ISy
На рис. 5 представлена структурная схема для реализации уравнения электромагнитного момента:
![]()

Рис. 5. Математическая модель определения электромагнитного момента M
Механическая угловая скорость вращения вала двигателя (рис. 6):
![]()

Рис. 6. Математическая модель определения механической угловой скорости вращения вала двигателя
Электрическая скорость вращения ротора (рис. 7):
![]()

Рис. 7. Математическая модель определения электрической скорости вращения ротора
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными IS – ΨR на выходе апериодических звеньев в системе абсолютных единиц приведена на рис. 8. Параметры асинхронного двигателя рассмотрены в работах [3] и [4].
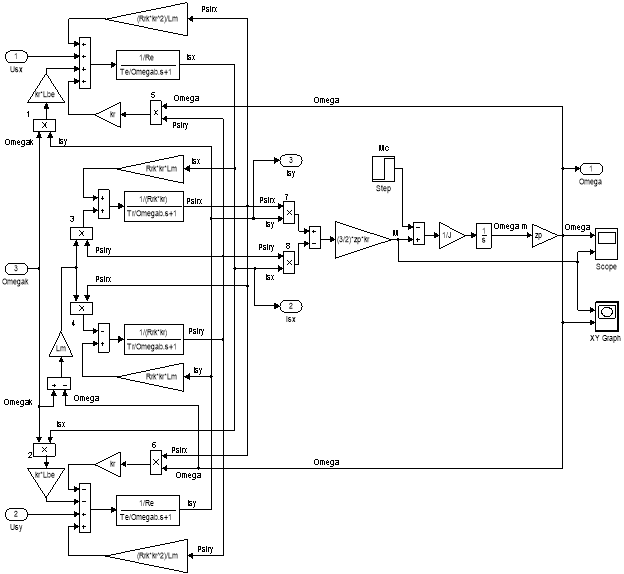
Рис. 8. Математическая модель асинхронного двигателя с переменными ΨR–IS на выходе апериодических звеньев в системе абсолютных единиц
Развернутая схема САР скорости системы «АИН ШИМ – АД» приведена на рис. 9. Под каждым элементом схемы указаны его номер и название.
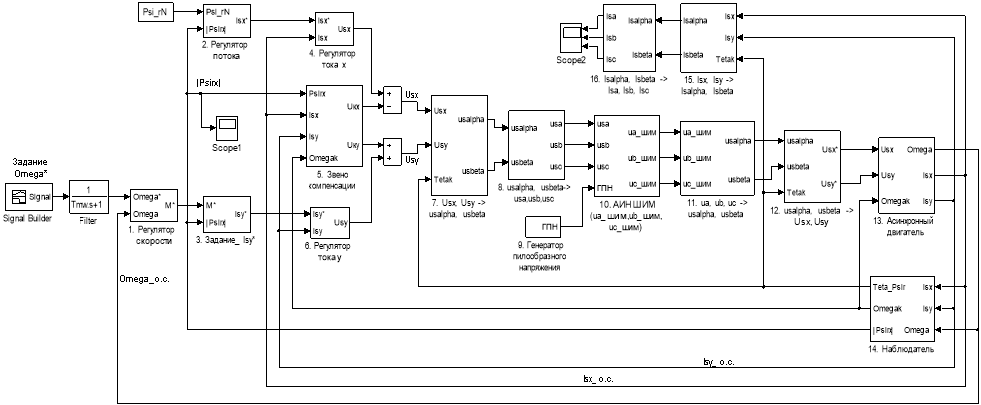
Рис. 9. Математическая модель САР скорости системы «АИН ШИМ – АД»
В контурах тока по проекциям x и y были получены одинаковые передаточные функции объектов управления:
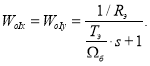
Синтез регуляторов тока производится по классической схеме [2]:
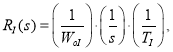
где ![]() - компенсация объекта;
- компенсация объекта;
![]() - исключение статической ошибки;
- исключение статической ошибки;
![]() - введение новой постоянной времени контура тока.
- введение новой постоянной времени контура тока.
Передаточная функция фильтра:
![]()
Принимаем настройку на модульный оптимум ![]() , тогда передаточные функции регуляторов тока по проекциям x и y:
, тогда передаточные функции регуляторов тока по проекциям x и y:
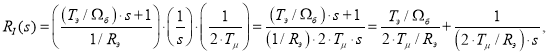
где Tμ - некомпенсируемая постоянная времени (примем Tμ = 0,0005 с).
Обозначим:
![]()
![]()
Математические модели ПИ-регуляторов тока по проекциям x и y под номерами 4 и 6 приведены на рис. 10 и 11.
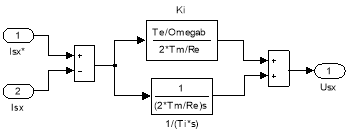
Рис. 10. ПИ-регулятор тока по проекции x
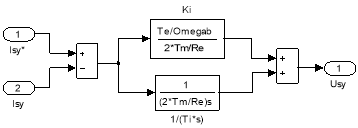
Рис. 11. ПИ-регулятор тока по проекции y
Важной частью структуры является наблюдатель, который служит для вычисления амплитуды и углового положения вектора потокосцепления ротора. Поскольку в системе x, y поток ориентирован по оси x, определим модуль |ΨRx|, исключив из уравнения (7) составляющую потока ΨRy:
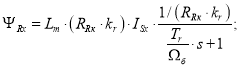
|
|
(16) |
Таким образом, модуль потока ротора связан с x-составляющей тока статора через передаточную функцию апериодического звена [6].
Из уравнения (14) выразим ![]() при ΨRy = 0:
при ΨRy = 0:
![]()
![]()
![]()
Интегрируя ![]() , можно получить угол потока ротора ΨRx [6].
, можно получить угол потока ротора ΨRx [6].
Математическая модель наблюдателя потокосцепления ротора (номер 14) приведена на рис. 12.
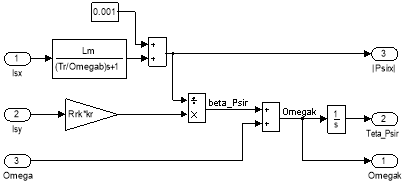
Рис. 12. Модель наблюдателя потокосцепления ротора
Приведем структурную схему контура потока ротора (рис. 13).
Рис. 13. Структурная схема контура потока ротора
При определении регулятора потокосцепления учтем следующее:
‒ до тех пор, пока поток ΨRx не установится, нельзя включать сигнал задания на задатчик интенсивности, т.е. Ω = 0;
‒ напряжение Usx близко к нулю.
Из (16) передаточная функция объекта управления в контуре потока будет иметь следующий вид:
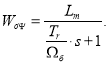
Передаточная функция регулятора потока:
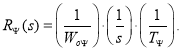
Примем ![]() , где n = 1; 2; 10; 20. Тогда передаточная функция регулятора потока определится следующим образом:
, где n = 1; 2; 10; 20. Тогда передаточная функция регулятора потока определится следующим образом:
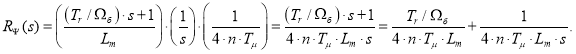
Выразим коэффициенты ПИ-регулятора потока:
![]()
![]()
Модель ПИ-регулятора потока под номером 2 представлена на рис. 14.
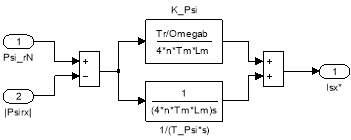
Рис. 14. ПИ-регулятор потока
В контуре скорости передаточная функция объекта имеет следующий вид:
![]()
Синтез регулятора скорости:
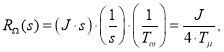
где ![]()
Математическая модель П-регулятора скорости (номер 1) приведена на рис. 15.
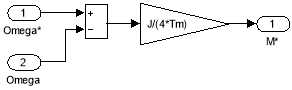
Рис. 15. Пропорциональный регулятор скорости
В системе управления предусмотрена компенсация внутренних перекрестных связей. Из уравнений (8) и (15) выразим компенсационные составляющие каналов управления:
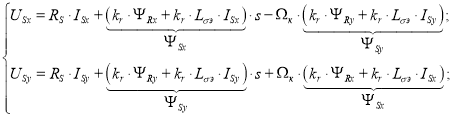
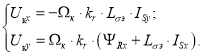
Математическая модель компенсации перекрестных связей (номер 5) представлена на рис. 16.
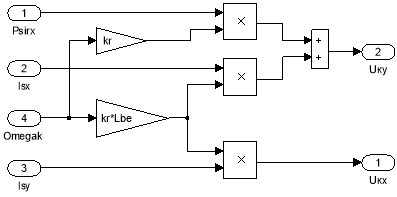
Рис. 16. Компенсация внутренних перекрестных связей
Задание на скорость Ω* формируется в блоке Signal Builder (рис. 17).
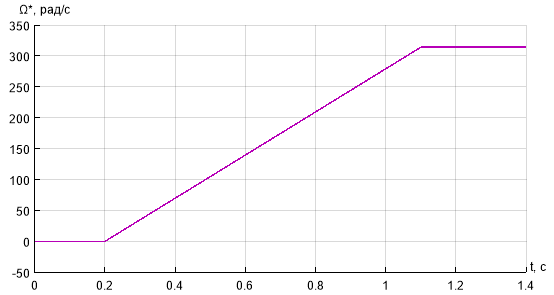
Рис. 17. Сигнал задания на скорость Ω*
Номинальное потокосцепление ротора в абсолютных единицах в соответствии с [3] определяется по следующей формуле и при векторном управлении поддерживается постоянным:
![]()
где 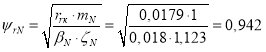 - номинальное потокосцепление ротора в относительных единицах;
- номинальное потокосцепление ротора в относительных единицах;
![]() - базовое значение потокосцепления.
- базовое значение потокосцепления.
Задание на статорный ток по проекции y:
![]()
Отсюда ![]()
Математическая модель определения задания ![]() (номер 3) дана на рис. 18.
(номер 3) дана на рис. 18.
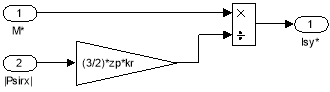
Рис. 18. Реализация задания статорного тока ![]() по проекции y
по проекции y
Преобразователи координат на развернутой схеме САР скорости под номерами 7 и 8 (![]() и
и ![]() ) приведены на рис. 19 и 20 [4].
) приведены на рис. 19 и 20 [4].
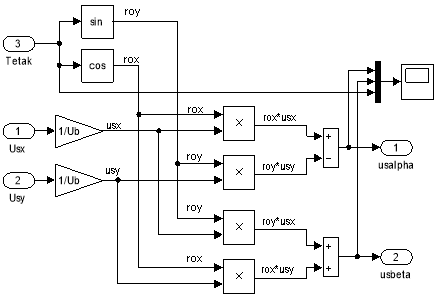
Рис. 19. Преобразователь координат: USx, USy → usα, usβ
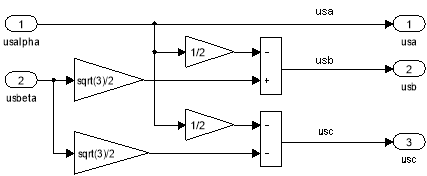
Рис. 20. Преобразователь координат: usα, usβ → usa, usb, usc
Математические модели АИН ШИМ (номер 10) и генератора пилообразного напряжения ГПН (номер 9) даны на рис. 21 и 22. Работа АИН ШИМ была рассмотрена нами в статьях за 2016 г.

Рис. 21. Генератор пилообразного напряжения (ГПН)
Преобразователи координат под номерами 11 и 12 (![]() и
и ![]() ) даны на рис. 23 и 24.
) даны на рис. 23 и 24.
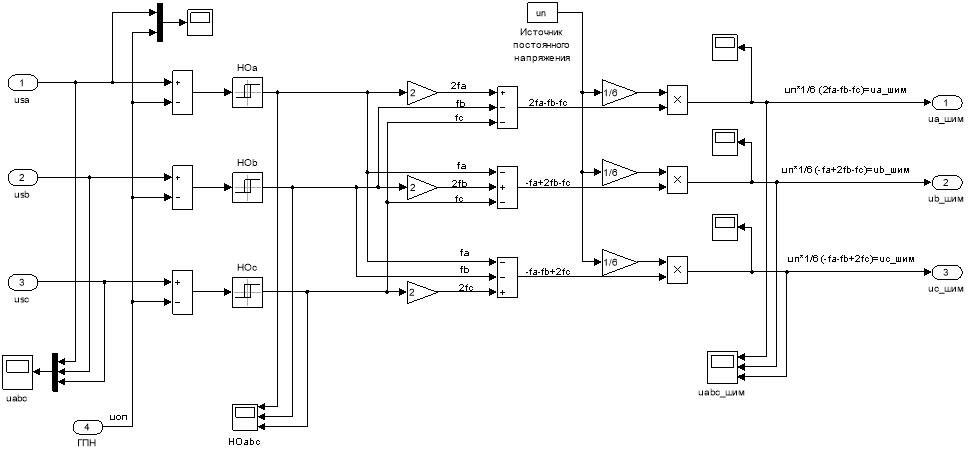
Рис. 22. Математическая модель АИН ШИМ
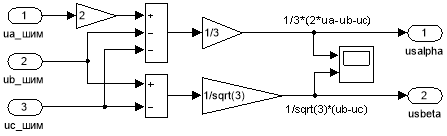
Рис. 23. Преобразователь координат: uа шим, ub шим, uc шим → usα, usβ
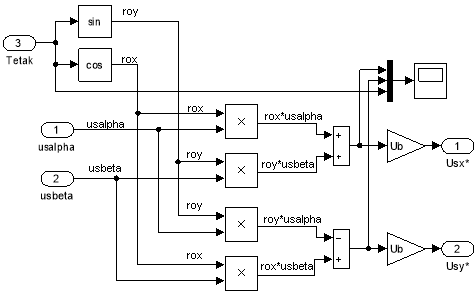
Рис. 24. Преобразователь координат: usα, usβ → USx, USy
Обратные преобразователи координат по статорным токам с номерами 15 и 16 на развернутой схеме САР скорости приведены на рис. 25 и 26 [4].
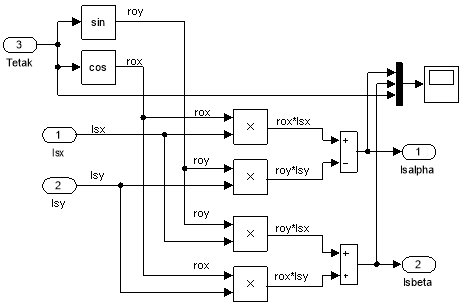
Рис. 25. Обратное преобразование (1-я ступень): ISx, ISy → ISα, ISβ
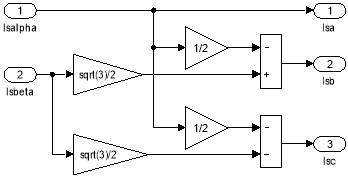
Рис. 26. Обратное преобразование (2-я ступень): ISα, ISβ → ISa, ISb, ISc
Расчет параметров производим в Script:
|
PN=320000; UsN=380; IsN=324; fN=50; Omega0N=104.7; OmegaN=102.83; nN=0.944; cos_phiN=0.92; zp=3; Rs=0.0178; Xs=0.118; Rr=0.0194; Xr=0.123; Xm=4.552; J=28; Ub=sqrt(2)*UsN; Ib=sqrt(2)*IsN; |
OmegasN=2*pi*fN; Omegab=OmegasN; Omegarb=Omegab/zp; Zb=Ub/Ib; Psib=Ub/Omegab; Lb=Psib/Ib; kd=1.0084; Mb=kd*PN/OmegaN; Pb=Mb*Omegarb; rs=Rs/Zb; lbs=Xs/Zb; lbr=Xr/Zb; lm=Xm/Zb; Lm=lm*Lb; kr=lm/(lm+lbr); SsN=3*UsN*IsN; ZetaN=SsN/Pb; |
betaN=(Omega0N-OmegaN)/Omega0N; lbe=lbs+lbr+lbs*lbr*lm^(-1); Lbe=lbe*Lb; roN=0.9962; rrk=roN*betaN; Rrk=rrk*Zb; Tr=lm/(rrk*kr); re=rs+rrk*kr^2; Re=re*Zb; Te=kr*lbe/re; Psi_rN=1.612; n=20; un=2.2; Tm=0.0005; Tmw=0.001; |
Числовые значения параметров выводятся в окне Workspace (рис. 27).
Рис. 27. Числовые значения параметров в окне Workspace
Результаты моделирования САР скорости системы «АИН ШИМ – АД» приведены на рис. 28, …, 31.
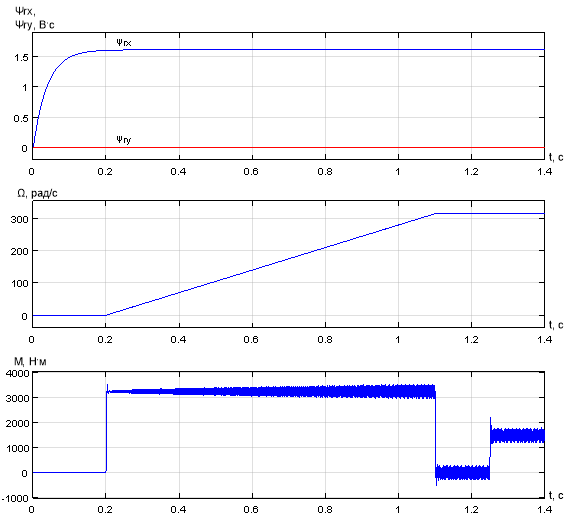
Рис. 28. Графики потокосцеплений, скорости и электромагнитного момента при ![]() и fоп = 10 кГц
и fоп = 10 кГц
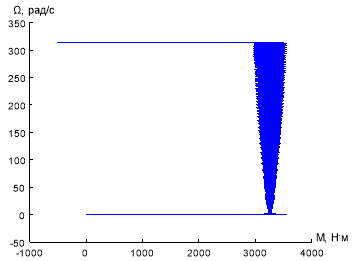
Рис. 29. Динамическая механическая характеристика при ![]() и fоп = 10 кГц
и fоп = 10 кГц
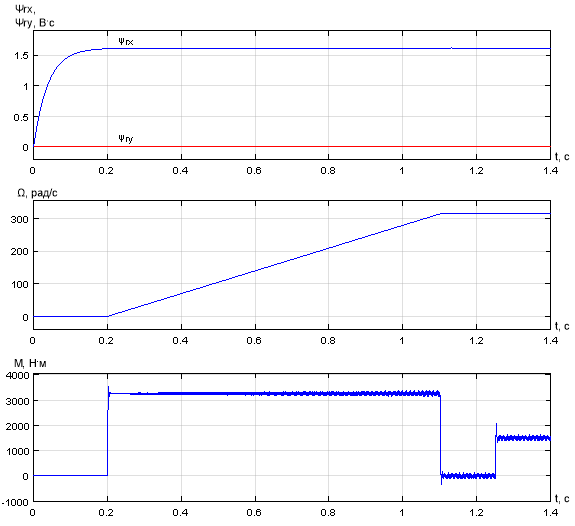
Рис. 30. Графики потокосцеплений, скорости и электромагнитного момента при ![]() и fоп = 30 кГц
и fоп = 30 кГц
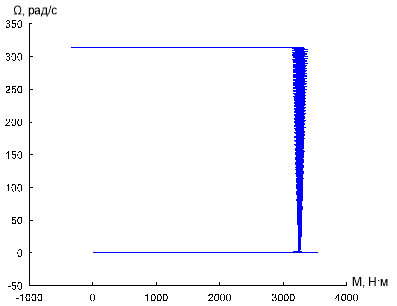
Рис. 31. Динамическая механическая характеристика при ![]() и fоп = 30 кГц
и fоп = 30 кГц
Литература:
- Емельянов А.А., Гусев В.М., Пестеров Д.И., Даниленко Д.С., Бесклеткин В.В., Быстрых Д.А., Иванин А.Ю. Моделирование САР скорости асинхронного двигателя с переменными ΨR - IS с контуром потока в системе абсолютных единиц // Молодой ученый. — 2018. — №13. — С. 22-40.
- Шрейнер Р.Т. Системы подчиненного регулирования электроприводов: учеб. пособие / Р.Т. Шрейнер. - Екатеринбург: Изд-во ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. – 279 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электроприводы переменного тока на базе непосредственных преобразователей частоты с ШИМ: монография / Р.Т. Шрейнер, А.И. Калыгин, В.К. Кривовяз; под. ред. Р.Т. Шрейнера. - Екатеринбург: ФГАОУ ВПО «Рос. гос. проф.-пед. ун-т», 2012. – 223 с.
- Калачёв Ю.Н. Наблюдатели состояния в векторном электроприводе. - М.: Самиздат, 2015. - 80 с.