Создана математическая модель для определения модуля упругости ячеистого заполнителя типа «гипар» при сжатии.
Ключевые слова: трехслойная конструкция, ячеистый заполнитель, математическая модель, модуль упругости
Одним из важнейших направлений снижения массы конструкции ЛА и других технических объектов является внедрение технологий трехслойных конструкций, элементы которых состоят из двух несущих обшивок, соединенных легким заполнителем [1]. Главной особенностью трехслойной конструкции является значительно больший момент инерции поперечного сечения, чем в конструкции той же массы [2]. Наиболее распространенным типом заполнителя, использующимся в трехслойных конструкциях, является сотовый заполнитель [3]. Но с этим заполнителем возникают трудности при изготовлении криволинейных панелей или панелей с переменной толщиной [4]. Для изготовления таких панелей предлагается ячеистый заполнитель.
Заполнитель ячеистого типа (Рис. 1) представляет собой регулярные структуры, состоящие из однотипных чашеобразных элементов — ячеек, образующих полости, изолированные друг от друга и с одной стороны от обшивки. [5]
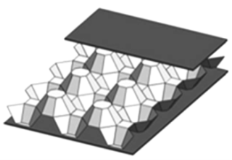
Рис. 1. Ячеистый заполнитель
Ячеистый заполнитель — состоящий из однотипных чашеобразных элементов, поэтому рассматривается только один повторяющийся элемент. Повторяющийся элемент ячеистого заполнителя показан на рис. 2.
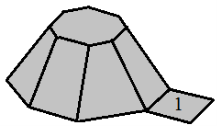
Рис. 2. Повторяющийся элемент ячеистого заполнителя
Определяется модуль упругости, потому что в композиционной конструкции соотношение модуля упругости к массе определяет эффективность конструкции. Чем больше этого соотношения, тем больше эффективности.
Допустим, что сила, действующая на трехслойной конструкции, принимается стенками. Еще допустим, что часть 1 (см. рис. 2) недвижна. Рассматриваются стенки ячейки как консольные балки. С помощью метода энергии определяется деформации балки. После этого рассчитается модуль упругости ячеистого заполнителя.
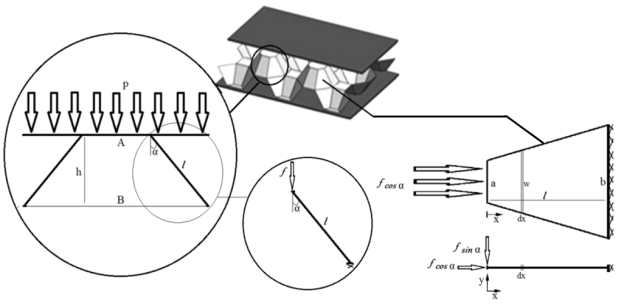
Рис. 3. Сила, действующая на повторяющемся элементе
|
F |
Сила, действующая на повторяющемся элементе |
|
f |
Сила, действующая на одной стенке |
|
P |
Давление, действующее на трехслойной конструкции |
|
S1 |
Площадь большого восьмиугольника |
|
a |
Длина маленького восьмиугольника |
|
b |
Длина большого восьмиугольника |
|
h |
Высота ячейки |
|
l |
Высота стенки |
|
α |
Угол отклонения ячейки |
|
t |
Толщина заготовки |
|
w |
Ширина поперечного сечения стенки |
|
M |
Изгибающий момент |
|
X1 |
Перемещение вдоль оси y |
|
X2 |
Перемещение вдоль оси x |
|
X |
Общее перемещение |
|
Ep |
Модуль упругости заготовки |
|
E |
Модуль упругости ячеистого заполнителя |
|
I |
Момент инерции сечения консольной балки |
|
Mp |
Масса одного повторяющегося элемента |
|
V |
Объем повторяющегося элемента |
|
|
Плотность заготовки |
Приводится метод энергии для определения деформации балки.
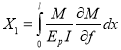 (1)
(1)
Где М — изгибающий момент, который определится нижеуказанным образом:
![]() (2)
(2)
Где f — сила, действующая на одной стенки, которая равна одной восьмой части силы, действующей на одной элементе. Потому что у каждого элемента есть восемь стенок.
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Где p — напряжение или давление, действующее на трехслойной конструкции. А S1 — площадь, на которой действует эта сила. После этого, определится момент инерции сечения консольной балки. Для консольной балки с прямоугольной сечением, момент инерции определится ниже указанным образом:
![]() (6)
(6)
Для консольной балки с трапецией формой изменение ширины поперечного сечения стенки нижеуказанной формулой:
![]() (7)
(7)
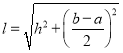 (8)
(8)
С помощью уравнений 1, 2, 3, 6, 7 определится перемещение вдоль оси y:
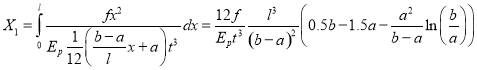 (9)
(9)
После определения перемещения вдоль оси y, определится перемещения вдоль оси х:
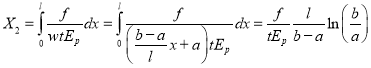 (10)
(10)
А теперь определится общее перемещение по перпендикулярной оси к конструкции:
![]() (11)
(11)
![]() (12)
(12)
помощью уравнений 4, 5, 9, 10, 11 модуль упругости определится нижеуказанным образом:
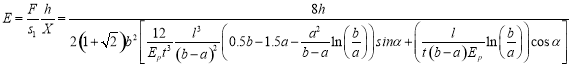 (13)
(13)
В этом разделе рассматривается фактор, определяющий эффективность композиционного материала. Этим фактором является соотношение упругости к массе конструкции. Здесь рассматривается соотношение модуля упругости к массе одного повторяющегося элемента.
![]() (14)
(14)
Где ρp — плотность заготовки и V — объем повторяющегося элемента, который определится нижеуказанным образом.
![]() (15)
(15)
С помощью уравнений 8, 12, 13, 14,15 определится фактор, определяющий эффективность легкого композиционного ячеистого заполнителя:

Фактор, определяющий эффективность ячеистого заполнителя зависит от свойств заготовки (t, ρp, Ep) и геометрии ячейки (a, b, h). С помощью вышеуказанного соотношения определяются оптимальные геометрии ячейки и свойства заготовки. Заметим, что этот фактор при проектировании должен быть как можно максимальным.
Выводы
В этой статье создали математическую модель для определения модуля упругости ячеистого заполнителя. После этого рассчитали соотношение модуля упругости к массе, чтобы определить оптимальные свойства и геометрические параметры для проектирования ячеистого заполнителя.
Литература:
- Gibson LJ, Ashby MF. Cellular solids. Cambridge: Cambridge University Press; 1999 [Chapter 8].
- Meguid SA, Cheon SS, Abbasi NE. FE modelling of deformation localization in metallic foams. Finite Elem Anal Des 2002;38(7):631–43.
- Belingardi G, Cavatorta MP, Duella R. Material characterization of a composite-foam sandwich for the front structure of a high speed train. Compos Struct 2003;61(1–2):13–25.
- Kindervater CM, Georgi H. Composite strength and energy absorption as an aspect of structural crash resistance. In: Structural crashworthiness and failure, 1993. p. 189–235.
- Zupan M, Chen C, Fleck NA. The plastic collapse and energy absorption capacity of egg-box panels. Int J Mech Sci 2003;45(5):851–71.







