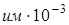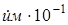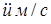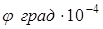В работе предложено решение вертикального и крутильного колебания вязкоупругого полупространства при применении идеи комплексных модулей упругости. Уравнение движения механической системы получено на основе принципа Даламбера.
Ключевые слова: колебания, волны расширения, вязкоупругое полупространство, скальная порода, уравнение движения.
Колебания основания - одна из главных задач, имеющих всестороннее техническое применение, например, в таких областях, как фундаменты под стенки, разного вида конструкции дорожных покрытий и аэродромов и т. п. Решение проблемы вертикального и крутильного колебаний упругого полупространства было представлено, в частности, в работе О.Я. Шехтер [1]. В настоящей работе предложено решение проблемы вертикального и крутильного колебания вязкоупругого полупространства при примении идеи комплексных модулей упругости. Предлагаемая работа посвящена проблеме динамической совместной работы конструкции с основанием при сейсмических действиях, распространяющихся из уровня горного массива через слоистую групповою среду по направлению к конструкции. Внимание сосредоточивается на экстремальном случае действия вертикально распространяющихся поперечных сейсмических волн, их отражений и переходов через слоистую среду грунта. Уравнение движения распространения волн имеет следующий вид:
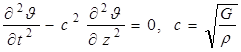 (1)
(1)
где G — модуль сдвига; r — плотность материала. Решение дифференциального уравнения (1) [1] запишем следующим образом:
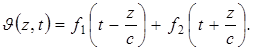 (2)
(2)
На границе z = 0: 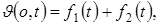 т. е.
т. е. 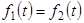 , тогда
, тогда 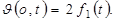
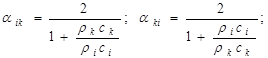
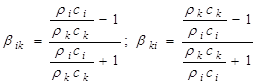 .
.
Решения разработано для n-слойной системы в течение исследования изменений во времени приходящих и отходящих волн от гранулы слоев, на скальной породе и на поверхности грунта. Для одно- и двухслойной системы решение приспособлено для вычислительной точки зрения менее трудной версии, при которой исследуются изменения во времени колебаний на уровне скального массива, и на поверхности грунта. Для строительной конструкции — жесткого фундамента при горизонтально действующем сейсмическом движении разработаны две версии расчета. В первой версии, проблема колебаний жесткого фундамента решается классическим способом, т. е. отдельно при нагружении сейсмическим ускорением на поверхности грунта 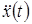 при отношении.
при отношении.
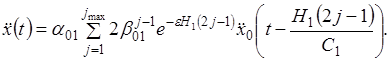
Вторая версия состоит в том, что в нагрузочном сейсмическим ускорении 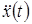 учитываются и действия вторичных отраженных волнений в грунтовой среде, вызванных колебанием конструкции. Расчет колебания фундамента осуществляется с помощью уравнений
учитываются и действия вторичных отраженных волнений в грунтовой среде, вызванных колебанием конструкции. Расчет колебания фундамента осуществляется с помощью уравнений
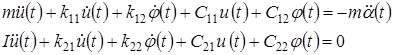 (3)
(3)
где 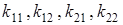 — коэффициенты демпфирования;
— коэффициенты демпфирования; 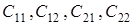 — коэффициент жесткости. Уравнения (3) являются линейными и легко решаются аналитическим путем. Результаты расчетов представлены в таблице.
— коэффициент жесткости. Уравнения (3) являются линейными и легко решаются аналитическим путем. Результаты расчетов представлены в таблице.
|
x |
|
|
|
|
|
0,30 0,15 0,0 |
0,206 0,198 0,210 |
0,047 0,058 0,079 |
0,238 0,256 0,288 |
0,128 0,136 0,146 |
Для получения численного решения мы использовали следующие исходные данные 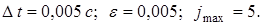 Таким образом, в работе разработаны методы для расчета многослойного фундамента, при воздействии динамических нагрузок.
Таким образом, в работе разработаны методы для расчета многослойного фундамента, при воздействии динамических нагрузок.
Литература:
1. О. Я. Шехтер. Об учете инерционных свойства грунта при расчете вертикальных вынужденных колебаний массивных фундаментов//НИИ Симн.12, Вибрации оснований и фундаментов, Москва, 1948.
2. G. N. Bycroft. Forced Vibrations of rigid circular plate on a semi infinite elastic space and on an elastic stratum// Phil. Trans. Roy. Soc. London, Sen.A, 248, 1956, 327–368.
3. Рашидов Т. Р. Динамическая теория сейсмостойкости сложных систем подземных сооружений.-Ташкент. Фан.1973.-182с.
4. Бозоров М. Б., Сафаров И. И., Шокин Ю. И. Численное моделирование колебаний диссипативно однородных и неоднородных механических систем. СО РАН, Новосибирск, 1966.- 188с.
5. Рашидов Т. Р., Хожиметов Г. Х., Мардонов Б. М. Колебания сооружений, взаимодействующих с грунтом. – Ташкент. Фан. 1975.-174с.
6. Т. О. Жўраев. Жураев Т. О. Нестационарные колебания деформируемого полупространства при воздействии взрывных нагрузок. -Т.: «Fan va texnologiya», 2013, 112стр.
7. Жўраев Т. О. Цилиндрические защитные сооружения при воздействии взрывных нагрузок // Проблемы механики, № 1, 2005. -с. 52–55.
8. Сафаров И.И, Едгоров У. Т., Жураев Т.О., Джумаев З. Ф. Об установившихся колебаниях трехслойных цилиндрических тел // Проблемы механики. 2000. № 1, -с. 31–34.
9. Сафаров И. И., Едгоров У. Т., Жураев Т.О Численный анализ статической жесткости амортизаторов-втулок // Проблемы механики. 1999 № 1, -с.42–46
10. Ахмедов Ш. Р., Жураев Т. О., Жумаев З. Ф. Воздействие плоской продольной упругой волны на выемки треугольного профиля // Проблемы механики. —№ 3. -2000. -с.53–55.