В статье рассматриваются явные формулы многомерной хаотической интерполяции функций многих переменных. Для них приводится оценки остаточных членов в зависимости от класса интерполируемых функций.
Ключевые слова: многомерная хаотическая интерполяция, оценки остаточных членов, зависимость остаточного члена от класса функций.
In the article, we consider interpolation formulas of many variable’s and discussing estimate of remainder for class of functions.
Задача интерполяции является одной из основных задач численных методов. С её помощью решаются задачи приближённого аналитического представления, дифференцирования, интегрирования таблично заданных функций или функций со сложным аналитическим представлением. В настоящее время она применяется в проектировании самолётов, кораблей, деталей сложной формы, в компьютерной графике.
Задача интерполяции для функций многих переменных ставится так. В области 
m-мерного евклидова пространства 
, заданы точки (узлы) интерполяции 
, и значения некоторой функции 
(1)
Требуется найти интерполяционную функцию, 
такую, что выполнялись условия интерполяции (совпадения значений в узлах интерполяции):
(2)
До 1960 годах в основном рассматривалась задача интерполяции функции от одной переменной. Интерполяционная формула строилась в виде линейной комбинации чебышевской системы функций, т. е. в виде
, (3)
для которой, задача (2) для любых множества точек интерполяции разрешима однозначно.
Самыми известными формулами интерполяции являются формулы Ньютона, Лагранжа, Гаусса,Эрмита, Стирлинга, Бесселя, Эверетта, Тиле. Приведем интерполяционные формулы Ньютона и Лагранжа вместе с остаточным членом:
, (4)
, (5)
.(6)
Здесь 
- разделённые разности.
Мы рассмотрим обобщения одномерных формул интерполяции Ньютона и Лагранжа. Введём обобщённые интерполяционные формулы Ньютона и Лагранжа [1]:
(7)
, (8)
где 
-норма в
. Вводим обобщённую разделённую разность:
. (9)
Для обобщённой интерполяционной формулы Ньютона известен вид остаточного члена [1]
. (10)
В статье для интерполяционных формул (4),(5), (7),(8) определяются остаточные члены, в зависимости от класса 
интерполируемых функций 
.
Из формулы (8) найдём следующую интерполяционную формулу. Достаточно, чтобы было
. Для этого, отбросим числовой знаменатель, и принимаем
.
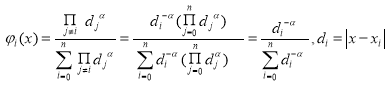Так появляется интерполяционная формула Шепарда:
.
2. Оценки остаточных членов одномерной полиномиальной интерполяции
Введём обозначения:
, 
,
, 
.
Тогда ясно, что справедливы оценки
.
Докажем простую лемму, упрощающую понимание основной теоремы.
Лемма 1. Пусть 
Тогда справедливы оценки
.
Доказательство. Имеем
.
Перемножаем все эти равенства, переходим к модулю и извлекаем n+1-корень. В результате получаем утверждение. Аналогично, получаем следующее утверждение.
Теорема 1. Пусть 
Тогда справедливы формула и оценка
. (11)
Доказательство. По формуле (6) находим, что для любых последовательности узел
справедлива формула
.
Перемножим эти формулы по
, переходим к модулю и получаем, что
.
Теперь извлекаем корень и имеем
.
Используя неравенство 
находим основное неравенство теоремы:
.
3. Представление для разделённых разностей
Для разделённых разностей (9) при
получим одно важное соотношение.
Лемма 2. Пусть
. Тогда существуют точки 
и направления
такие, что справедливо представление для разделённых разностей
Здесь последнее равенство означает связь производной Гато и Фреше [3].
Доказательство. Применим метод индукции. Шаг к=1,2.По определению имеем
,
.
Шаг 
-й. Пусть теперь 
. Шаг 
й. Имеем
4. Оценки многомерной явной интерполяции.
Множество узлов (сетку) обозначим через
. Далее введём обозначения:
,
.
Тогда ясно, что 
, 
, 
.
Лемма 3. Пусть 
Тогда справедлива оценка
.
Доказательство аналогично доказательству леммы 1. Имеем
.
Перемножаем все эти равенства, переходим к модулю и извлекаем n+1-корень. В результате получаем утверждение. Аналогично, получаем следующее утверждение.
Теорема 2. Если
, то справедлива оценка
(12)
Доказательство. По формуле (10) для любых последовательности узлов справедлива формула
.
Перемножая эти формулы для , имеем 
.
Переходим к модулю, извлекаем корень и находим 
.
Привлекая неравенство находим основное неравенство:
.
Литература:
- Имомов А. Явные интерполяционные формулы для функций многих переменных. Методы сплайн функций. Тезисы докл. Новосибирск, Изд. ИМ, 2001, с.38–39.
- Имомов А. Явные формулы многомерной интерполяции. Молодой учёный. № 19(99) октябрь-1, 2015.
- Зорич В. А. Математический анализ. т.II.М.: Наука, 1984. -640 с.
