Математическое моделирование методики измерения параметров изделий из пьезоматериалов

Вводные замечания

Многие приборы и устройства различного назначения основаны на использовании пьезоэлектрического эффекта, создаваемого пьезокерамическими преобразователями. В настоящее время применение пьезокерамических элементов широко распространено в медицине (приборы УЗИ, получение различных взвесей), в системах охранной сигнализации (датчики подвижных объектов), в дальномерных системах гидро- и радиолокации, в различных устройствах техники связи. Электрические фильтры с пьезорезонаторами обладают значительно более высокими электрическими характеристиками, чем LC-фильтры.

Другим перспективным применением пьезокерамических элементов является ультразвуковое воздействие на изделия радиоэлектронной и механической промышленности с целью удаления с их поверхности загрязнений и продуктов технологического процесса. Ультразвуковая очистка в сравнении с механической является более экологически перспективной, так как она позволяет автоматизировать технологический процесс и благодаря этому повысить производительность очистного оборудования и качество очистки.

Такое широкое применение стимулирует проведение исследовательских и опытно-конструкторских работ по пьезокерамике и развитие промышленного производства пьезокерамических изделий. При производстве изделий из пьезокерамики необходимо производить оперативный контроль их характеристик [1]. Пьезорезонаторы характеризуются множеством параметров, однако среди них можно выделить основные – резонансные частоты, параллельную емкость (С) и тангенс угла диэлектрических потерь (tgd). Определив эти параметры, а также геометрические размеры пьезорезонатора, можно рассчитать все остальные его параметры.

Данная работа посвящена анализу работы корреляционного измерителя емкости и тангенса угла диэлектрических потерь пьезорезонаторов в условиях производственных помех методами статистического моделирования, с целью выбора оптимальных технических параметров и характеристик измерителя. При корреляционном методе измерения величины С и tgd определяются по результатам прохождения гармонического колебания A₀cos(ωt)  через пьезорезонатор и эталонный резистор.

 

Корреляционный измеритель С и tgd

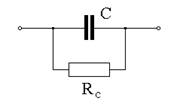
На рис.1 представлена схема замещения пьезоэлемента в виде двухполюсника, с достаточной для практики точностью описывающая его свойства на низких частотах вдали от резонансной области.

Рис.1. Схема замещения пьезоэлемента

Адмитанс [1] этого двухполюсника составляет:

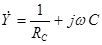                                                                 ,                                                           (1)

а тангенс угла диэлектрических потерь определяется отношением:

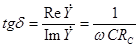                                                             .                                                      (2)

Значение величины tgd в диэлектриках обычно мало (10^-2¸10^-4), что приводит к определенным сложностям при ее измерении.

На фоне аддитивных гауссовых помех, которыми моделируются погрешности измерений, оптимальной процедурой является корреляционная обработка результатов измерения, которая заключается в следующем.

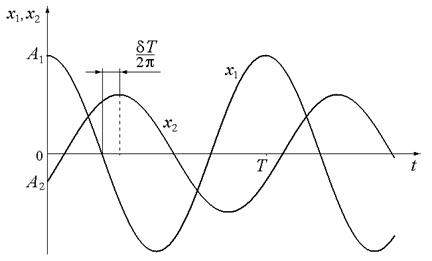
На периоде колебаний Т вычисляется взаимная энергия [2,3] двух гармонических сигналов одной частоты (см. рис.2)

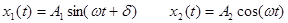                                         ,                                  (3)

где d ‑ угол диэлектрических потерь:

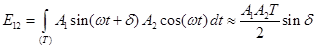                                       .                                (4)

Рис.2. Рабочие сигналы измерителя

С учетом энергий сигналов (3) за период Т:

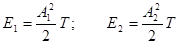                                                             (5)

из соотношения (4) для малых значений угла потерь (d<<1) получим:

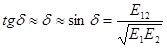                                                                (6)

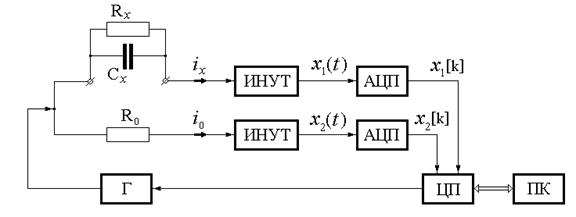
Структурная схема измерителя, иллюстрирующая принцип его работы, представлена на рис.3. Управление работой прибора осуществляется персональным компьютером (ПК), взаимодействующим с центральным процессором (ЦП) измерителя. Гармонический сигнал 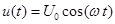 с генератора (Г) подается одновременно на измеряемый двухполюсник и на эталонный резистор R₀.

Рис.3. Структурная схема измерителя

Токи, протекающие через измеряемый элемент (i_x) и образцовый резистор (i₀)

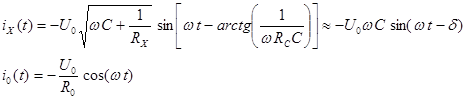                                  (7)

преобразуются с помощью источника напряжения, управляемого током (ИНУТ), в сигналы (3). Аналого-цифровой преобразователь (АЦП) переводит эти сигналы в цифровую форму; отсчеты сигналов передаются в ПК для дальнейшей обработки.

Для построения ИНУТ важно использовать микросхемы операционных усилителей (ОУ), совмещенные в одном корпусе, что обеспечит идентичность параметров ОУ, минимизацию вносимого ими фазового сдвига.

После преобразования сигналов x₁(t) и x₂(t) в цифровую форму, производятся следующие операции:

1) Центрирование выборок x₁[k]  и  x₂[k]:

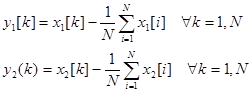                                                                                        (8)

где N – объем выборки, x[k] – оцифрованный сигнал, y[k] – центрированный сигнал.

2) Формирование значений сумм  S₁, S₂  и S₁₂  из центрированных выборок y₁[k] и y₂[k]:

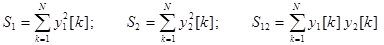                                                       (9)

3) Расчет значений емкости и тангенса угла диэлектрических потерь:

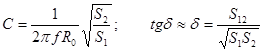                                                                                    (10)

 

Результаты математического моделирования

Для оценки потенциальной помехоустойчивости измерителя в условиях помех было произведено математическое моделирование его работы.

К исходным сигналам (3) был добавлен белый гауссов шум с дисперсией σ² и нулевым средним:

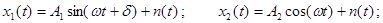                                                   (11)

амплитуды A₁ и A₂ для простоты полагались равными.

Моделирование проводилось по следующим параметрам: разрядность АЦП, соотношение шум/сигнал q = σ/A, число выборок на период сигнала, число периодов сигнала, используемых для расчета, величина угла потерь. Для учета влияния разрядности АЦП и частоты взятия выборок производилась квантование сигналов по амплитуде и дискретизация по времени. Начальная фаза гармонических сигналов выбиралась равновероятно случайным образом. Значения x[k] вычислялись как среднее значение сигнала х(t) за время преобразования:

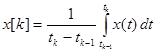                                                                                                   (12)

После дискретизации значений в соответствии с заданной разрядностью АЦП вычислялись суммы (9):

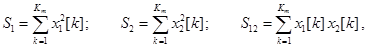                                                          (13)

где      K_m = FT = Nn,

F – частота дискретизации АЦП,

T – длительность оцифровываемого сигнала,

n– число отсчетов, приходящихся на один период сигнала,

N – число оцифровываемых периодов сигнала.

Следует отметить, что число периодов N, используемых для расчета, должно быть целым, иначе в сигнале может появиться постоянная составляющая, искажающая результат.

По полученным значениям сумм в соответствии с соотношениями (10) вычислялось значения величин С_j и d_j. В результате многократных прогонов (j=1,М; M=100¸1000) определялась среднеквадратическая погрешность:

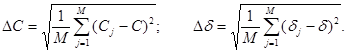                                                               (14)

Влияние величины d на точность его измерения при отсутствии шумов представлено на рис.4.

Рис.4. Систематическая погрешность метода в зависимости от величины d

Из рисунка видно, что при d < 0.1 можно получить высокую (до 10^-4) точность измерений.

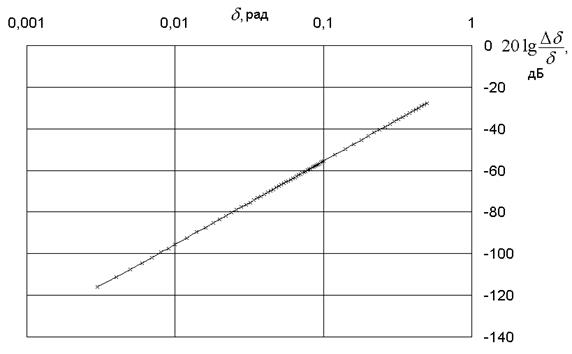
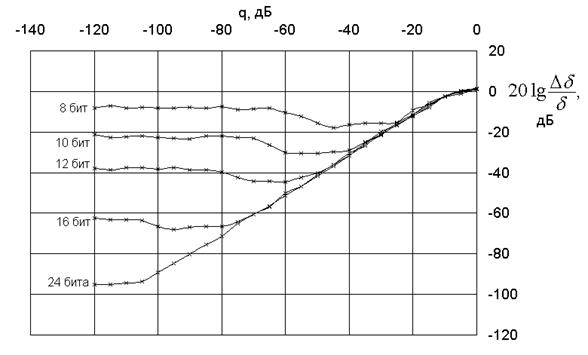
На рис.5. изображена зависимость относительной ошибки измерения d в зависимости от отношения шум/сигнал и от разрядности АЦП.

Рис.5. Зависимость погрешности  d от соотношения шум/сигнал и разрядности АЦП

Как видно из графика, ошибка уменьшается пропорционально уменьшению соотношения шум/сигнал до определенного предела, определяемого разрядностью АЦП. Таким образом, АЦП вносит в сигнал шум дискретизации.

Для получения высокой точности измерений целесообразно использовать АЦП с разрядностью не ниже 16.

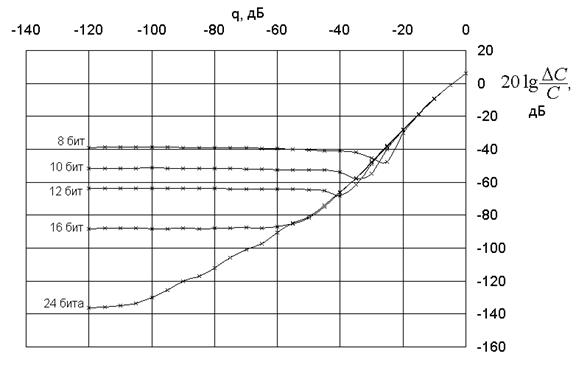
На рис.6. приведена та же зависимость для ошибки измерения емкости.

Рис.6. Зависимость погрешности измерения С от соотношения шум/сигнал и разрядности АЦП

Характер зависимостей тот же, однако график спадает значительно резче, чем в случае с углом потерь. Графики на рис.5 и 6 получены при d = 0.01, N=10, n=100.

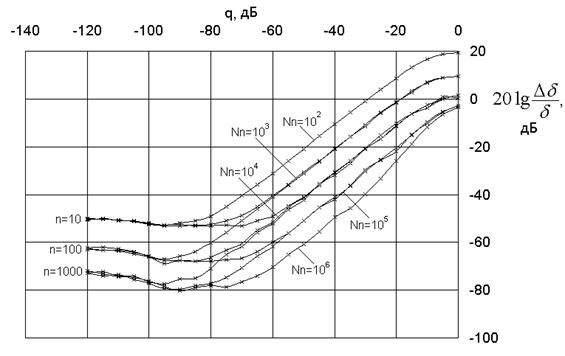
Рис.7 иллюстрирует влияние числа выборок на период сигнала и числа периодов на характер зависимости ошибки измерения d от соотношения шум/сигнал.

Рис.7. Зависимость погрешности d от соотношения шум/сигнал и числа выборок

Положение кривой на графике определяется произведением Nn, т.е. суммарным числом выборок. Однако, при малых соотношениях шум/сигнал определяющим становится лишь число выборок на период сигнала. Таким образом, при отсутствии шума нет смысла наращивать число периодов в целях повышения точности измерений.

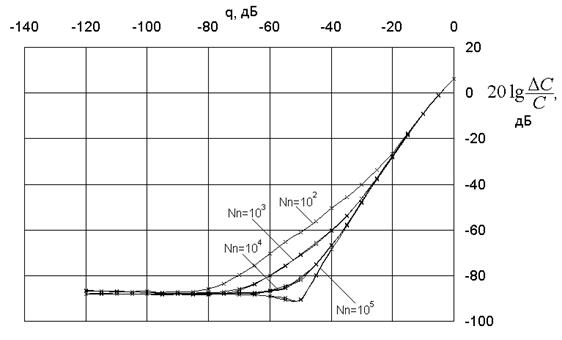
На рис.8 приведены аналогичные зависимости для погрешности измерения емкости.

Рис.8. Зависимость погрешности С от соотношения шум/сигнал и числа выборок

Вид графика определяется только произведением Nn (суммарным числом отсчетов сигналов). Графики на рис. 7,8 получены при разрядности АЦП – 16 бит, d = 0.01.

На рис.9,10 изображены зависимости относительных ошибок измерения емкости и угла потерь от числа отсчетов на период сигнала (частоты дискретизации АЦП).

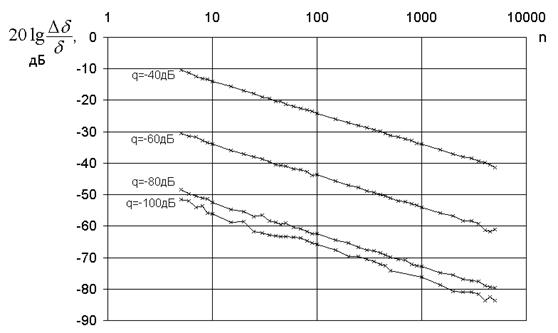
Рис.9. Зависимость погрешности d от числа выборок на период сигнала

Видно, что увеличение последней монотонно снижает погрешность измерения угла потерь при любом соотношении шум/сигнал, причем неограниченно снижает. Таким образом, увеличивая частоту дискретизации, можно получить необходимую точность измерения тангенса угла потерь.

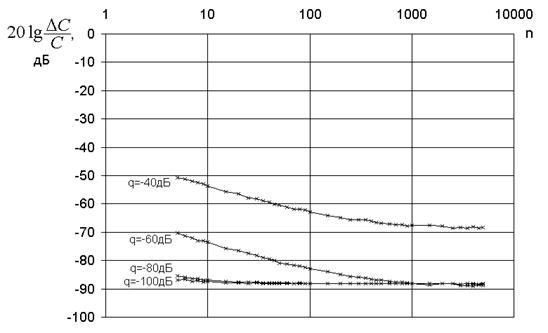
Xарактер зависимостей для емкости (рис.10) аналогичен, однако здесь имеет место ограничение по частоте дискретизации, выше которого увеличение последней не приводит к повышению точности.

Рис.10. Зависимость погрешности С от числа выборок на период сигнала

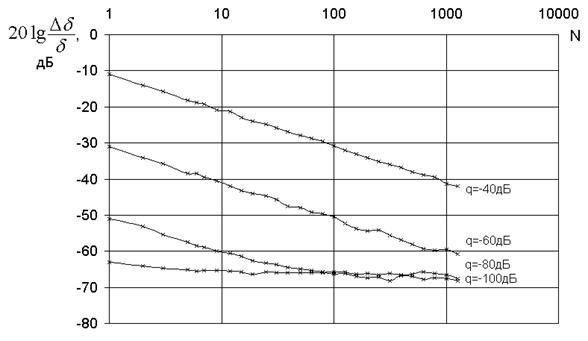
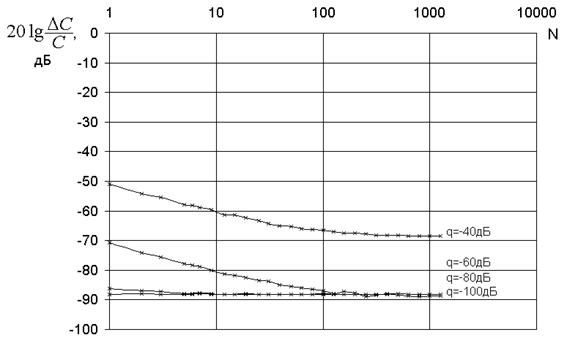
На рис.11,12 изображены зависимости относительных ошибок измерения емкости и угла потерь от числа периодов сигнала, используемых для расчетов.

Рис.11. Зависимость погрешности d от числа используемых периодов сигнала

Рис.12. Зависимость погрешности С от числа используемых периодов сигнала

Графики аналогичны рис.9,10, однако здесь ограничение присутствует как для емкости, так и для угла потерь. Увеличивать число периодов в целях повышения точности измерений целесообразно только при большом уровне помех.

Выводы

Таким образом, корреляционный метод позволяет получить высокую точность измерения емкости и тангенса угла диэлектрических потерь (~10^-4 для d < 0.1 и до ~10^-6 при d < 0.01) при следующих параметрах измерителя:

- разрядность АЦП – 16 бит;

- число периодов сигнала, использованных для измерения – 20;

- число отсчетов АЦП на период сигнала – 100;

- соотношение шум/сигнал – -60 дБ.

Точность измерений при больших значениях отношения шум/сигнал может быть повышена путем увеличения длительности измерения. Взаимодействие с персональным компьютером позволит автоматизировать обработку результатов измерений при большом количестве контролируемых изделий.

 

Библиографический список

1.      Кушнир Ф.В. Электрорадиоизмерения. – Л : Энергоатомиздат, 1983. – 320 с.

2.      Баскаков С.И. Радиотехнические цепи и  сигналы:  Учебник  –  М: Высшая школа, 1983. – 225 с.

3.      Гоноровский И.С. Радиотехнические цепи и сигналы. – М: Сов. радио, 1977. – 512 с.

4.      Ратхор Т.С. Цифровые измерения. Методы и схемотехника. М.: Техносфера, 2004. – 376 с.

5.      Глазунов Р.В., Васильев А.Ф.,Захарченко В.Д., Игнатьев А.Н. Измерение параметров нагруженного пьезоэлемента // Материалы международной научной конференции «Информационные технологии в современном мире» – часть 4 – Таганрог: ТРТУ, 2006, с. 4-6.