Целью данной работы является вывод математического аппарата, описывающего процессы в асинхронном двигателе, в доступной для понимания студентами форме. Открытия сделанные учеными в 1940–50 г.г. при исследовании асинхронных двигателей оказывают потрясающие воздействия. В данной работе сделана попытка реконструкции хода исследовательской мысли ученых и передачи студентам специфической красоты в движениях математических формул. Пройти школу на материалах такого наследия является важнейшим условием формирования будущих исследователей.
Вначале, на примере мгновенных трехфазных напряжений в косинусоидальной форме сдвинутых во времени на 120° с помощью формулы Эйлера (1707…1783 г.г.) преобразовываются в виде степенных функций. Переход к степенным функциям позволяет производить замену произведений множества тригонометрических формул в простые алгебраические суммы выражений находящихся в степени. Далее, используя известную формулу суммы от произведения мгновенных значений напряжений по фазам на соответствующие единичные векторы переходим к пространственному вектору напряжения статора вращающемуся с циклической частотой питающего напряжения (в данной работе рассматривается двухполюсный двигатель). Аналогично производится переход к пространственным токам статорных и роторных величин, причем фазовые сдвиги токов естественно отразятся в пространственном расположении векторов. В потокосцеплениях фаз статора и ротора показаны взаимосвязи от угла поворота магнитных осей. Перед взглядом студентов предстает множество уравнений с переменными коэффициентами. При переходе к пространственным векторам происходит существенное сокращение числа уравнений. Производные от угла поворота магнитных осей дают скорость вращения ротора.
1. Преобразование мгновенных значений напряжений в степенные функции
Мгновенные значения трехфазных напряжений описываются следующими зависимостями:
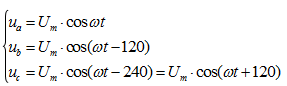 (1)
(1)
где 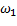 - циклическая частота напряжения, рад/c.
- циклическая частота напряжения, рад/c.
На рис.1 показана связь мгновенных значений напряжений 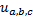 с векторами
с векторами 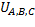 во временной системе координат, как их проекции на действительную ось
во временной системе координат, как их проекции на действительную ось 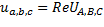 . Работа в векторной форме существенно ускоряет процесс исследования, причем в любой момент времени легко перейти к косинусоидальной форме мгновенных значений. Выполнить, например, произведение множества косинусоид (синусоид) представляет довольно трудоемкую задачу, а в векторной форме произвести перемножение значительно легче.
. Работа в векторной форме существенно ускоряет процесс исследования, причем в любой момент времени легко перейти к косинусоидальной форме мгновенных значений. Выполнить, например, произведение множества косинусоид (синусоид) представляет довольно трудоемкую задачу, а в векторной форме произвести перемножение значительно легче.
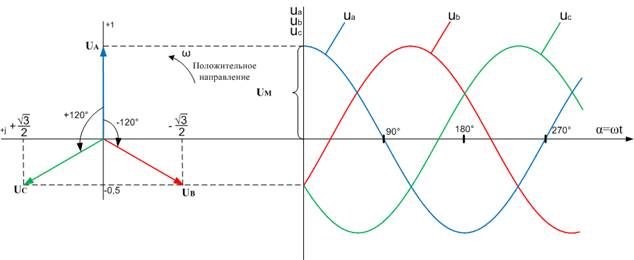
Рис. 1. Связь мгновенных значений напряжений с векторами соответствующими во временной системе координат
Не меньшую роль в ускорении процессов математических преобразований играет представление с помощью формулы Эйлера мгновенных значений в степенные функции.
Выразим систему уравнений 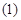 через степенные функции:
через степенные функции:
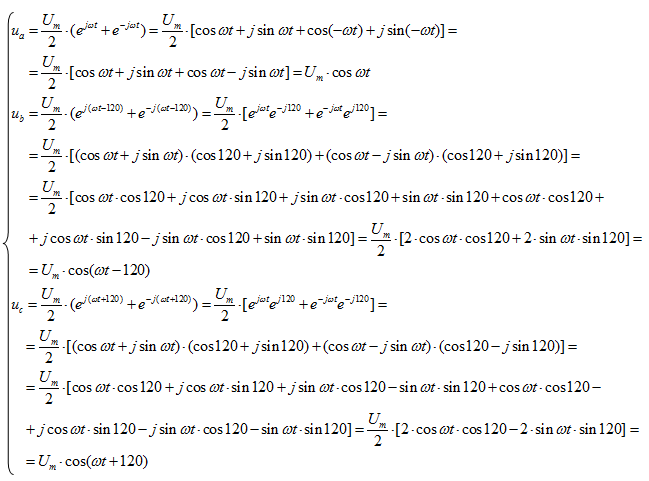
Итак, система уравнений в степенной форме имеет следующий вид:
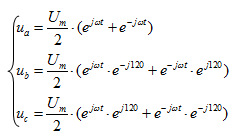 (2)
(2)
2. Переход от мгновенных значений напряжений к пространственному вектору 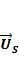
Пространственный вектор напряжения 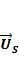 определяется по следующей зависимости:
определяется по следующей зависимости:
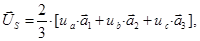
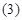
где 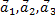 - единичные пространственные векторы.
- единичные пространственные векторы.
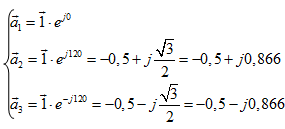 (4)
(4)
Подставив в уравнение 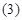 мгновенные значения напряжений в степенной форме
мгновенные значения напряжений в степенной форме  и единичные пространственные векторы
и единичные пространственные векторы  получим:
получим:
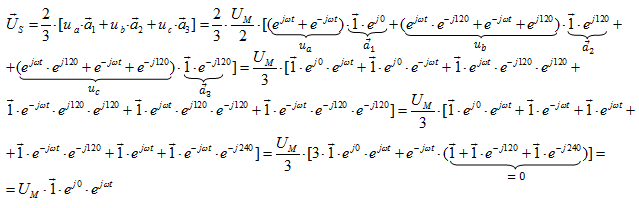
Геометрический смысл преобразования мгновенных значений напряжений в пространственный вектор показан на рис.2 (в электронном варианте все векторы и их проекции даны в цветном варианте).
Последовательность построений: во временной системе координат определяются мгновенные значения векторов на действительную ось 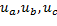 , далее они переносятся на действительную ось в пространственную систему координат в виде отрезков. Затем осуществляется разворот этих отрезков с помощью единичных пространственных векторов. Далее производиться геометрическая сумма
, далее они переносятся на действительную ось в пространственную систему координат в виде отрезков. Затем осуществляется разворот этих отрезков с помощью единичных пространственных векторов. Далее производиться геометрическая сумма 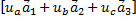 , и наконец, умножив полученный вектор на множитель
, и наконец, умножив полученный вектор на множитель 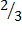 получим искомый вектор
получим искомый вектор 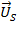 .
.
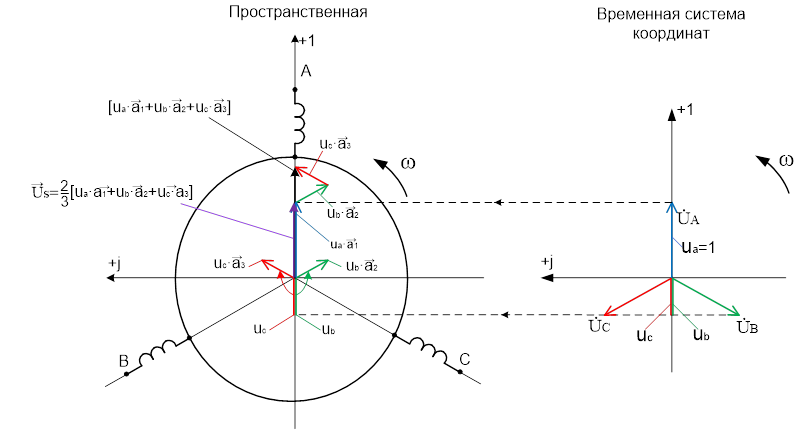
Рис. 2. Геометрический смысл построения пространственного вектора 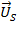 по составляющим
по составляющим 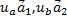 и
и 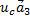
.
3. Основные уравнения асинхронного двигателя в фазных переменных статора и ротора
Обобщенная асинхронная машина показана на рис. 3.
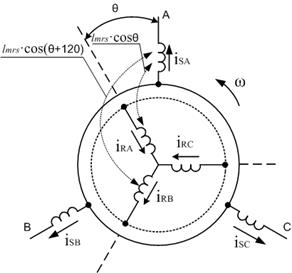

Рис.3. Обобщённая асинхронная машина
Rs, ls, lms — параметры статорной обмотки,
Rr, lr, lmr — параметры роторной обмотки,
|lmsr|=|lmrs|=|lm|–коэффициенты взаимоиндуктивности при совпадении магнитных осей статора и ротора 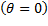 .
.
Баланс фазных напряжений статорных и роторных цепей:
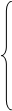
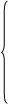
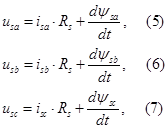
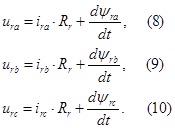
Потокосцепление фаз статорных и роторных цепей с учетом взаимоиндуктивностей с переменными коэффициентами, зависящими от расположения магнитных осей ротора и статора
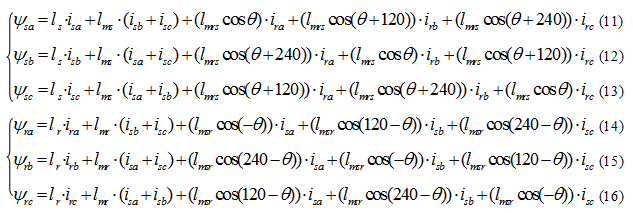
4. Преобразование балансов напряжений в фазных переменных в соответствующий баланс пространственных векторов.
Умножив обе части уравнения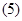 на единичный пространственный вектор
на единичный пространственный вектор 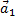 , уравнения
, уравнения 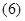 и
и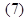 — соответственно на
— соответственно на 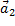 и
и 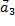 . Далее, просуммируем уравнения:
. Далее, просуммируем уравнения:
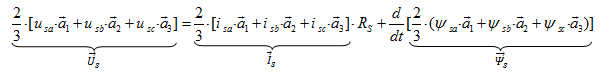
В векторной форме баланс напряжений для статора:
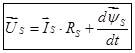
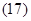
Аналогично, произведем преобразование баланса напряжений для роторных фазных переменных:
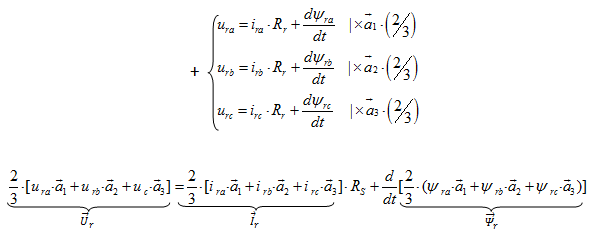
В векторной форме баланс напряжений для ротора:
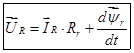
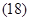
5. Вектор потокосцепления статора АД
Пространственный вектор потокосцепления статора:
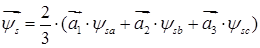 ,
, 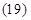
где 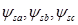 — мгновенные значения потокосцеплений статора;
— мгновенные значения потокосцеплений статора;
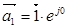 ,
, 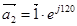 ,
, 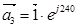 — единичные пространственные векторы.
— единичные пространственные векторы.
Уравнения 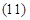 ÷
÷ 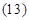 представим по трем столбцам соответствующих индуктивностей:
представим по трем столбцам соответствующих индуктивностей:
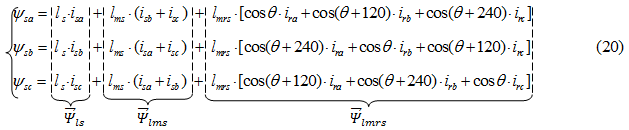
Первое уравнение умножим на единичный пространственный вектор 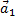 , второе — на
, второе — на 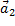 , и последнее уравнение
, и последнее уравнение 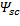 — на
— на 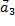 . С целью уменьшения громоздкости получаемых выражений вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем сумму в соответствии с формулой
. С целью уменьшения громоздкости получаемых выражений вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем сумму в соответствии с формулой 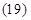 .
.
Переведем мгновенные значения токов статора и ротора с фазными переменными в степенные функции:
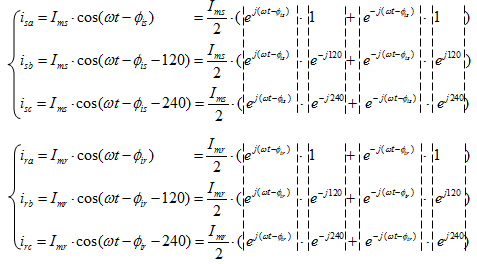
Аналогично, представим 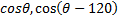 и
и 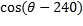 в степенной форме:
в степенной форме:
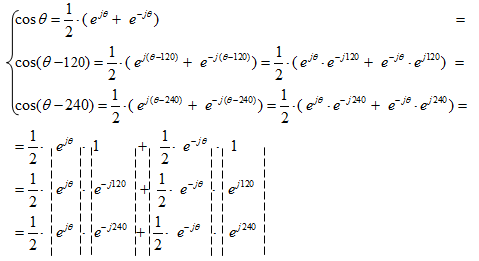
Или иначе, в удобной для запоминания форме:

Для первого столбца уравнение 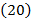 определим пространственный вектор
определим пространственный вектор 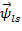 :
:
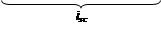
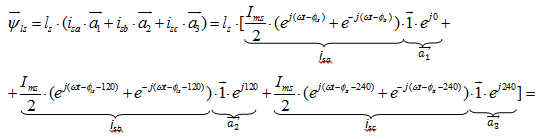
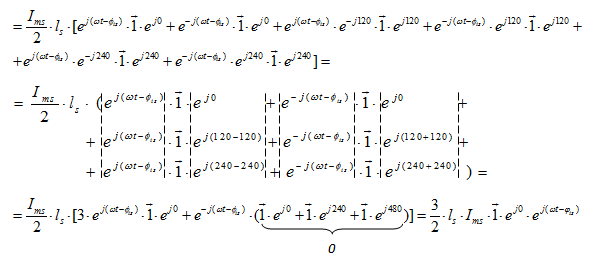
Потокосцепление 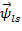 можно выразить в следующей форме:
можно выразить в следующей форме:
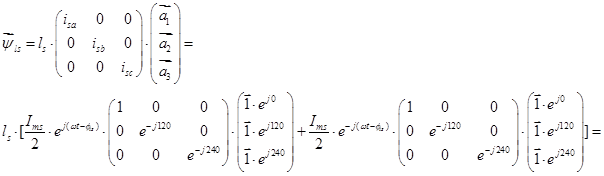
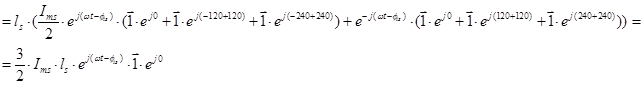 Для второго столбца:
Для второго столбца:
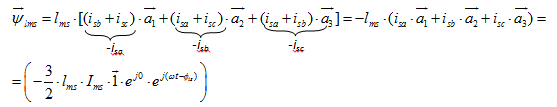
Наконец, для третьего столбца:
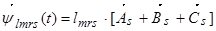 ,
,
где 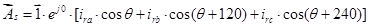
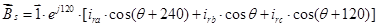
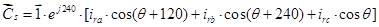
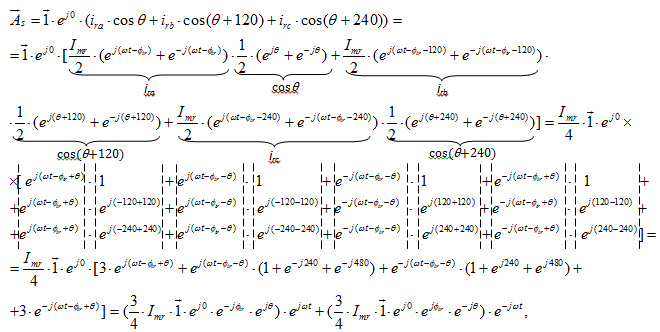
где 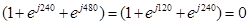

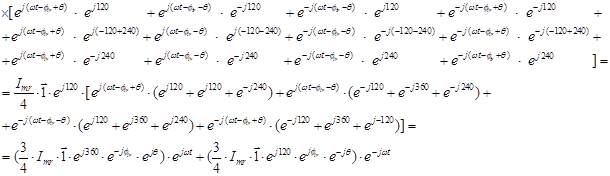

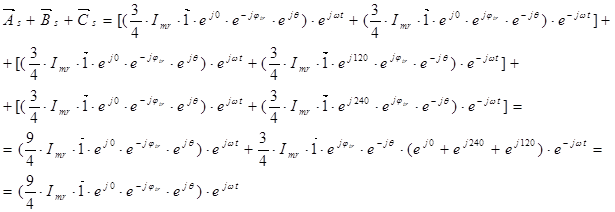
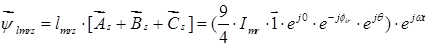
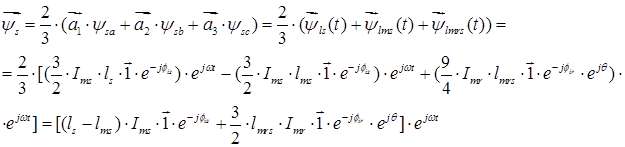 Обозначим
Обозначим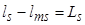 ;
; 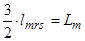 ;
;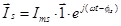 ;
; 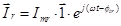 .
.
Окончательно, вектор потокосцепления статора [1]:
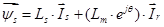
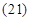
6. Вектор потокосцепления ротора АД
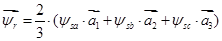 ,
, 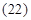
Уравнения (14) ÷ (16) представим по трём столбцам соответствующих индуктивностей:
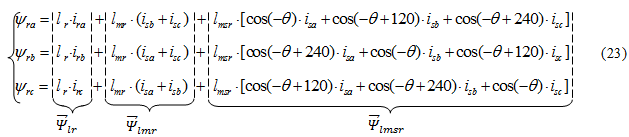
Первое уравнение умножим на 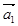 , второе — на
, второе — на 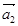 , третье — на
, третье — на 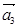 . Вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем полную сумму в соответствии с формулой (22).
. Вначале произведем суммирование отдельно по вертикальным столбцам, а затем приведем полную сумму в соответствии с формулой (22).
Пространственный вектор для первого столбца 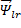 :
:

Пространственный вектор для второго столбца системы уравнений (23):
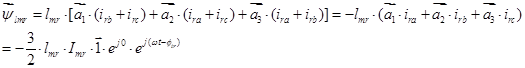
Пространственный вектор для третьего столбца (23):
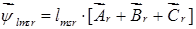 ,
,
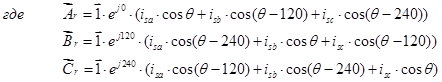
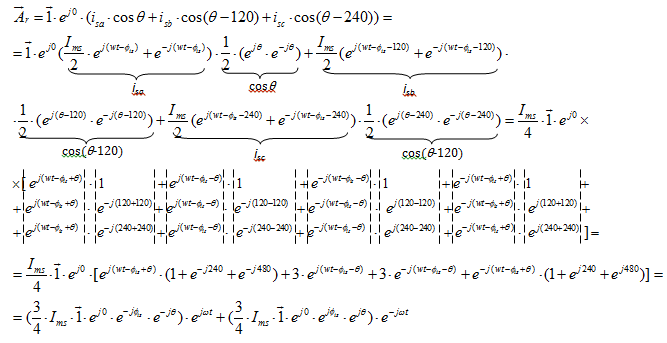
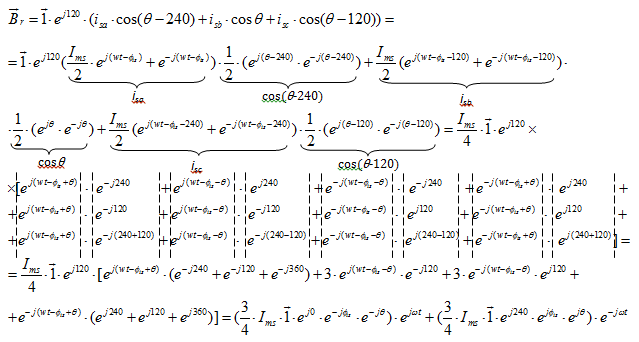
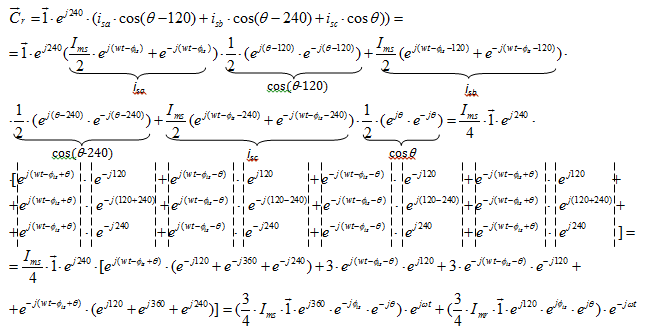
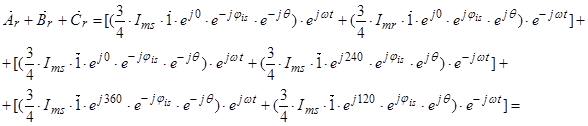
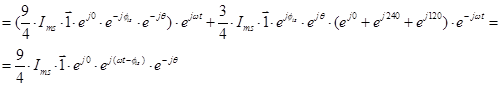
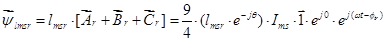
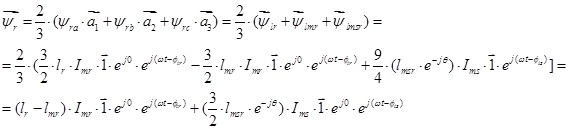
Обозначим 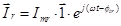 ;
; 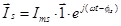 ;
; 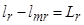 ;
; 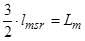 .
.
Окончательно, вектор потокосцепления ротора:
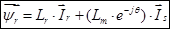 (24)
(24)
7. Векторные уравнения АД в различных системах координат
Основные уравнения асинхронного двигателя в векторной форме имеют вид:
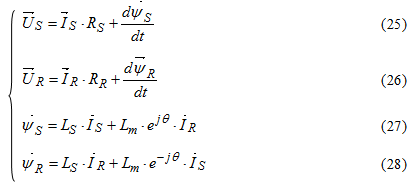
Сделаем существенное замечание по полученным обобщенным векторам. В уравнении (25) векторы 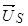 ,
, 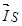 ,
, 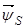 записаны в неподвижной системе координат статора, но в некоторых задачах их необходимо привести к другим системам координат. Рассмотрим схему преобразования одного из векторов, например,
записаны в неподвижной системе координат статора, но в некоторых задачах их необходимо привести к другим системам координат. Рассмотрим схему преобразования одного из векторов, например, 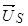 из одной системы координат в другую. Поясним это преобразование на следующем рис.4.
из одной системы координат в другую. Поясним это преобразование на следующем рис.4.
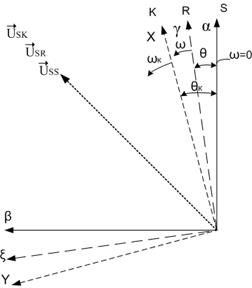
Рис.4. Система координат S.R.K.
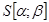 – неподвижная система координат статора (
– неподвижная система координат статора (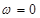 );
); 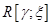 — система координат, связанная с ротором,
— система координат, связанная с ротором,
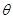 - угол сдвига системы координат R по отношению к S, причем
- угол сдвига системы координат R по отношению к S, причем 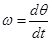 .
.
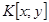 — произвольная система координат,
— произвольная система координат, 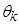 — угол сдвига к неподвижной системе
— угол сдвига к неподвижной системе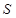 (
(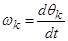 )
)
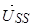 — пространственный вектор напряжения статора.
— пространственный вектор напряжения статора.
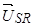 и
и 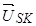 — этот же пространственный вектор напряжения статора в системах координат ротора
— этот же пространственный вектор напряжения статора в системах координат ротора 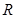 и
и 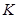 соответственно.
соответственно.
Связь между векторами в разных системах координат:
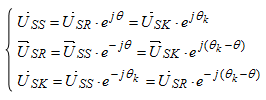
Система уравнений (25) — (28) примет следующий вид:
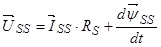 , (29)
, (29)
где 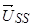 ,
, 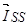 ,
, 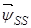 — записаны в не подвижной системе координат статора
— записаны в не подвижной системе координат статора 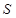 .
.
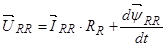 (30)
(30)
где 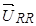 ,
, 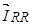 ,
, 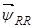 — пространственные векторы роторных величин в роторной системе координат R.
— пространственные векторы роторных величин в роторной системе координат R.
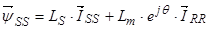 , (31)
, (31)
где 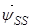 ,
, 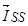 , — векторы потокосцепления и ток статора в неподвижной системе координат S, а
, — векторы потокосцепления и ток статора в неподвижной системе координат S, а 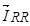 — в роторной системе координат сдвинутой в неподвижной системе на угол
— в роторной системе координат сдвинутой в неподвижной системе на угол 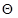 .
.
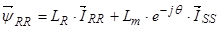 (32)
(32)
где 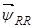 ,
, 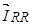 , — векторы потокосцепления и ток ротора в роторной системе координат R, а
, — векторы потокосцепления и ток ротора в роторной системе координат R, а 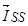 — в неподвижной системе координат
— в неподвижной системе координат 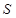 .
.
7.1 Приведение векторных уравнений к неподвижной системе координат статора
Уравнение (20) уже записано в статорной системе координат, поэтому показываем процесс приведения следующего уравнения. Для этого умножим обе части уравнение (21) на 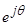 :
:
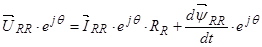 .
.
В соответствии с вышерассмотренной схемой приведения векторов из одной системы координат в другую, получим:
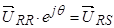 и
и 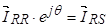 .
.
Выражение 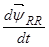 преобразуем к следующему виду:
преобразуем к следующему виду:
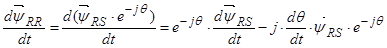
Окончательно 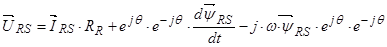 .
.
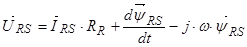
В выражении 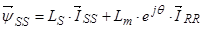 представим:
представим: 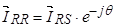 тогда
тогда
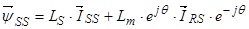
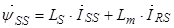 .
.
В уравнении (27) умножим обе части на 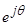 :
:
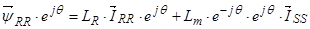 ,
,
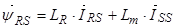 .
.
Окончательно уравнения (24) ÷ (27) в статорной системе координат примет следующий вид:
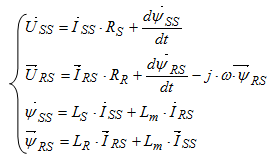
Опуская индекс «статорная система координат», получим:
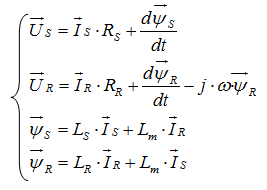 (33)
(33)
7.2 Приведение уравнений к роторной системе координат
Умножим обе части уравнение (24) на 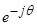 :
:
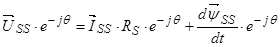
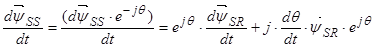
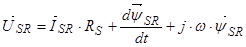
Уравнение (25) перепишем без изменений, т. к. оно уже записано в роторной системе координат:
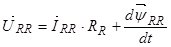
Уравнение (26) умножим обе части на 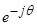 :
:
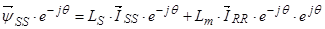 ,
,
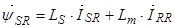
В уравнении (27) выразим 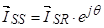 , тогда
, тогда
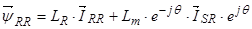 ,
,
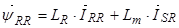
Окончательно в роторной системе координат уравнения (24) ÷ (27)имеют следующий вид:
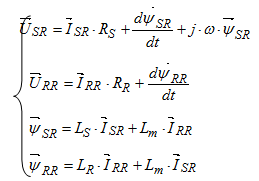
Опуская индекс «роторная система координат», получим:
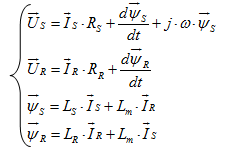 (34)
(34)
7.3 Приведение уравнений к системе координат вращающейся с произвольной скоростью 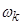
Уравнение (24) умножим на 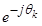 и сразу выразим
и сразу выразим 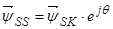 :
:
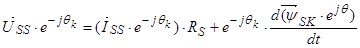 ,
,
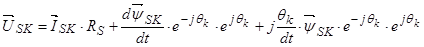 ,
,
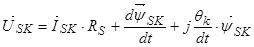 .
.
Уравнение (25) умножим на 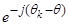 :
:
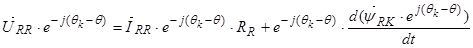 ,
,
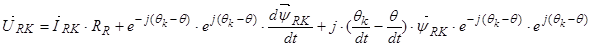
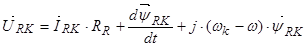 .
.
Уравнение (26) умножим на 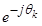 , тогда
, тогда
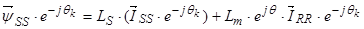 ,т. к.
,т. к. 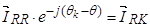 , то
, то
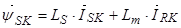 .
.
Уравнение(27) умножим на 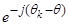 , тогда
, тогда
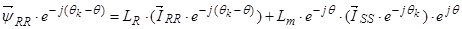
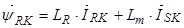 .
.
Для системы координат вращающейся с произвольной скоростью 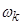 система уравнений:
система уравнений:
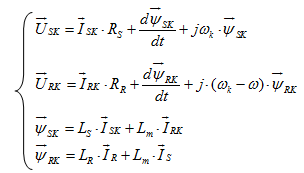
Опуская индекс «произвольная система координат», получим
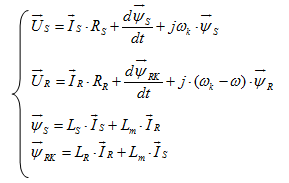 (35)
(35)
Литература:
1. Ковач К. П., Рац И. Переходные процессы в машинах переменного тока/Пер. с нем. М.Л.: Госэнергоиздат, 1963. 735 с.: ил.







