Исследование системы векторного управления частотно-регулируемым электроприводом переменного тока на виртуальной модели



В настоящее время частотно-регулируемый электропривод переменного тока становится главным типом регулируемого промышленного электропривода, серийно выпускаемого ведущими электротехническими компаниями.

Основным силовым преобразователем энергии такого электропривода являются полупроводниковые преобразователи частоты на полностью управляемых коммутируемых элементах типа силовых транзисторов (IGВT) и запираемых тиристоров (IGCT).

При разработке систем регулирования электроприводом различных производителей развиваются в одном направлении и, если на первом этапе развития (70-е годы прошлого века) использовались, преимущественно, законы частотного управления типа закона М. П. Костенко с коррекцией по напряжению в области низких частот, то на втором этапе (80-е годы) признание получили алгоритмы векторного управления [1].

Управление переходными процессами в машинах переменного тока основывается на необходимости организовать управление по переменным состояния: вектору тока статора i_s, вектору тока ротора i_r, потокосцеплению статора _s, потокосцеплению ротора _r, главному потокосцеплению машины _o = L_m (i_s + i_r). Эти переменные состояния взаимосвязаны перекрестными связями.

Базовым элементом такой системы управления приводом является преобразователь координат (векторный преобразователь). При помощи преобразователя координат осуществляется преобразование сигналов, пропорциональных переменным состояния (i_s, i_r, _r, _s, _o), из системы координат, жестко связанной со статором ( — ) или с ротором (d — q), во вращающуюся систему координат (1–2).

В [2] приведены алгоритмы управления АД, структурные схемы САУ и характеристики частотно-управляемого электропривода с асинхронным двигателем при управлении по вектору главного потокосцепления, по вектору потокосцепления ротора двигателя и по вектору магнитного потокосцепления статора асинхронного двигателя.

В последнее время наблюдается тенденция перехода к бездатчиковым системам с вычислением значений потокосцеплений по модели двигателя в реальном масштабе времени на основе применения быстродействующих вычислительных управляющих устройств.

В этом случае реализация закона _r = const имеет преимущественное значение [3].

Абсолютное скольжение, определяющее частоту тока ротора  = (₁ — ).

В режиме _r = const развиваемый электромагнитный момент не имеет максимума и растет неограниченно с ростом . Однако, при больших величинах скольжения поддержание неизменным _r невозможно из-за роста потокосцепления в воздушном зазоре и неизбежного насыщения машины. При изменении скольжения в пределах 3_ном увеличение _о незначительно и реализация _r = const вполне осуществима.

Имеется три основных способа реализации закона _r = const: скалярный, полярный и векторный.

Алгоритм управления в векторной форме имеет следующий вид:

,

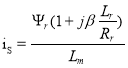а в полярной форме — следующий вид:

,

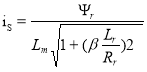 — угол между вектором потокосцепления _r и током i_s:

.

В схеме, реализующей векторный способ управления по абсолютному скольжению, регулирование тока осуществляется по двум каналам, которые соответствуют проекциям вектора на оси вращающейся системы координат, совмещенной с вектором потокосцепления ротора _r. При этом проекция на вещественную ось i_sх может поддерживаться постоянной или регулироваться в зависимости от скорости вращения для организации двухзонного регулирования АД. Проекция на мнимую ось i_sy изменяется пропорционально абсолютному скольжению .

В этом случае отсутствует электромагнитный переходный процесс по потокосцеплению ротора, который вызывает низкочастотные колебания в замкнутом по скорости электроприводе.

Таким образом, выбор закона управления электроприводом переменного тока с поддержанием _r = const можно считать наиболее приемлемым, что использовано в наиболее распространенных системах.

При построении микропроцессорной системы управления асинхронным электроприводом с преобразователем частоты, построенном на модулях с транзисторами IGBT и с широтно-импульсной модуляцией выходного напряжения задание амплитуды U_m и частоты ω_о выходного напряжения предпочтительно осуществлять в виде цифрового сигнала, а не в виде тригонометрических функций.

В связи с этим при моделировании асинхронного электропривода с векторным управлением целесообразнее использовать систему координат, в которой амплитуда и частота напряжения, приложенного к статорным обмоткам, присутствуют в явном виде. Такой системой координат является система координат, вращающаяся с частотой поля статора двигателя _о, то есть система координат (u — v) [4].

Если динамическая модель асинхронного двигателя выполнена в системе координат (u — v), вычисление модуля вектора потокосцепления ротора двигателя осуществляется по формуле:

после чего также определяются мгновенные значения косинуса и синуса угла γ для перевода переменных в систему координат (1–2):

Однако, поскольку обе системы координат и (u — v), и (1–2) вращается в пространстве с одинаковой частотой ω_о, координатное преобразование здесь представляет собой поворот одной системы координат по отношению к другой на некоторый пространственный угол до совмещения оси v с вектором потокосцепления ротора.

Раз обе системы координат неподвижны относительно друг друга, cosγ и sinγ представляют собой числовые значения соответствующих тригонометрических функций. Перевод составляющих вектора тока статора из системы координат (u — v) в систему координат (1–2) осуществляется с помощью уравнений:

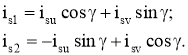
Далее строится двухканальная система регулирования, как и в предыдущем случае. Обратное преобразование координат также представляет собой поворот одной системы координат относительно другой на угол γ, но в противоположном направлении.

Канал регулирования потокосцепления ротора двигателя содержит внутренний контур регулирования составляющей тока статора i_s1 с ПИ-регулятором РТ1 и внешний контур регулирования модуля потокосцепления _{r m} с П-регулятором Р. На входе Р действует единичное постоянное задание.

Канал регулирования электромагнитного момента асинхронного двигателя содержит контур регулирования составляющей тока статора i_s2 с ПИ-регулятором РТ2 и контур регулирования скорости  с П-регулятором РС, на входе которого включен задатчик интенсивности (на структурной схеме не показан).

Структурная схема такой динамической модели системы векторного управления представлена на рис.1.

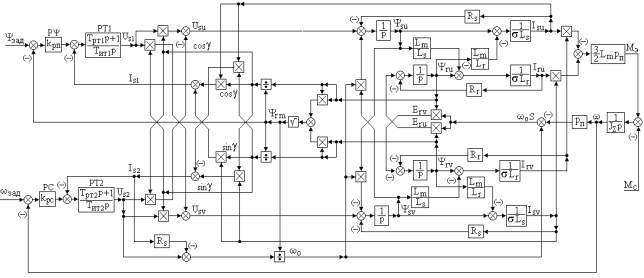Рис.1. Структурная схема модели системы векторного управления в осях (u — v)

Выходные сигналы регуляторов РТ1 и РТ2 пропорциональны составляющим вектора напряжения статора двигателя U_s1 и U_s2. Обратное преобразование координат для перехода из системы координат (1–2) в систему координат (u — v) имеет вид:

Напряжения U_su и U_sv представляют собой амплитудные значения и не содержат гармонических составляющих. Значение амплитуды выходного напряжения преобразователя частоты определяется следующим образом:

Значение частоты вращения системы координат, то есть частоты выходного напряжения преобразователя частоты, определяется следующим образом:

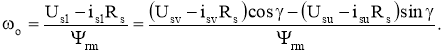
Таким образом, при реализации системы векторного управления с представлением модели асинхронного двигателя в системе координат (u — v) на выходе системы регулирования амплитуда и частота напряжения преобразователя частоты присутствуют в явном виде. Оптимальным с точки зрения реализации описанных алгоритмов является использование цифровых сигнальных процессоров (ЦСП), архитектура которых адаптирована для выполнения рекуррентных полиномиальных вычислений.

Решение системы уравнений, описывающих работу частотно­регулируемого привода — весьма трудоемкая задача. Для решения задач подобного рода существуют различные компьютерные технологии, в основе которых лежат пакеты прикладных программ. Наиболее распространенным среди таковых является пакет MATLAB с различными дополнениями, из числа которых Toolbox Simulink, удобный при проведении анализа электромеханических процессов, протекающих в электроприводе.

Основным достоинством этого дополнения является наличие библиотечных моделей, имитирующих практически все элементы, входящие в состав ЭП, в том числе и исполнительные двигатели. Поэтому для решения системы уравнений, моделирующих частотно­регулируемый привод, был выбран программный пакет Matlab Simulink.

Диаграммы электромеханических процессов, протекающих в компьютерной модели частотно­регулируемого ЭП с алгоритмом векторного управления по вектору главного потокосцепления, приведена на рис.2.

На приведенных диаграммах показаны процессы изменения напряжения U_s и тока I_s статора, частоты вращения ω, электромагнитного момента и модуля вектора главного потокосцепления |Ψ₀|, протекающие при пуске и равноускоренном разгоне АД до номинальной частоты вращения (рад/c), набросе и сбросе статического момента нагрузки (Нм), а также при равнозамедленном снижении частоты вращения АД до полной остановки.

Рис.2. Диаграммы электромеханических процессов

На основе полученных характеристик частотного привода можно оценить его энергопотребление в различных режимах работы и сравнить с энергопотреблением классического ступенчато регулируемого привода.

Литература:

1. Современный частотно-регулируемый электропривод /Горбань Р. Н., Янукович А. Т. — под редакцией Гаврилова А. В. — С-Петербург, СПЭК. 2001.
2. Дартау В. А., Рудаков В. В., Столяров И. М. Асинхронные электроприводы с векторным управлением -–Л.: Энергоатомиздат, Л.О., 1987.
3. Денисов К., Ермилов А., Карпенко Д. Способы управления машинами переменного тока и их практическая реализация на базе компонентов фирмы Analog Devices / CHIP NEWS. № 7–8, 1997.
4. Козярук А. Е., Рудаков В. В. Современное и перспективное алгоритмическое обеспечение частотно-регулируемых электроприводов. С.-Петербург, ГГИ(ТУ). -2002.