Фильтрационная схема подземного выщелачивание полезных ископаемых основана на использование постоянного или периодически действующего потока раствора реагента, заполняющего все трещины и открытые поры рудного тела.
Для определения поля скоростей необходимо определить поле давления. Распределения поля давления описываются дифференциальными уравнениями фильтрации [1].
Описываемое двумерное уравнение гидродинамики процесса ПВ при управлении в условиях применения этажной системы разработки в неоднородных средах из-за движения выщелачивающего раствора сверху вниз, придётся рассматривать математическую модель гидродинамики процесса ПВ в разрезе [2].
Таким образом, для определения распределения давления в фильтрационном потоке в условиях использования этажной системой разработки воспользуемся уравнением фильтрации [3,4]:
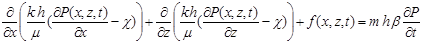(1)
для области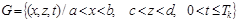 
,
с начальным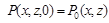
(2)
и граничными условиями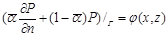 
. (3)
Здесь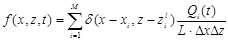 
.
Если предположим что координата х строго горизонтальна, составляющая силы тяжести по направлению оси х равна нулю, тогда уравнение (1) можно написать следующим виде:
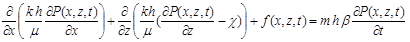(1’)
Трудности составления алгоритмов для численного решения (2.1)-(2.3) разностными методами во многом связаны с геометрией пласта. Поэтому целесообразно разрабатывать алгоритмы не для конкретных областей, а для более или менее широкого класса областей. Одним из возможных путей решения этой проблемы является замена краевой задачи (1)-(3) на задачу, в определенном смысле близкой к ней, но заданную в более простой области, например в виде прямоугольника. Такой метод называется методом фиктивных областей [71].
Применив идею метода фиктивных областей, заданную область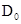 
включаем в стандартную прямоугольную область 
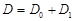с границей Г (рис. 1).
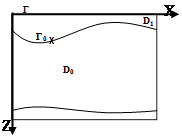
Рис. 1. Область расчета при применении метода фиктивных областей
В уравнении (1) введем следующие обозначения:
, 
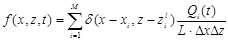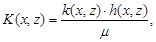
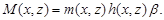
Тогда можно полагать, что задача (1)-(3) справедлива и в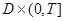 
:
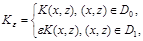
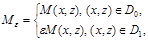
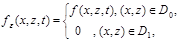
где D0 -заданная область с границей Г0; D1-фиктивная область; e-малое число порядка 10–3.
Решение задачи (1)-(3) сведем к последовательному решению одномерных задач соответственно вдоль строк и столбцов переходом с одного слоя на другой, что выражает основную идею экономичных методов. Эту же идею выражает неявная схема переменных направлений, предложенная в работах [1,2].
Сначала параметры, которые участвуют в уравнениях процесса, представляются в размерном виде, т. е. все величина уравнений имеют свои размерности. При применение конечно-разностных схем для решения уравнения (1)-(3) целесообразно вводить безразмерные переменные. Безразмерные переменные применительно к нашему случаю имеют вид:
,
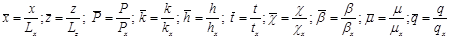где Lх, Lz, Px, kx,hx,bx,mx,qx tx, cx — некоторые характерные величины.
Подставляем безразмерные величины в уравнении (1):
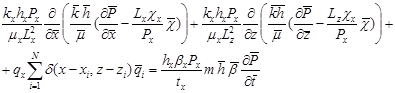
Разделяем оба части уравнении на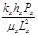 
и получим следующее уравнение:
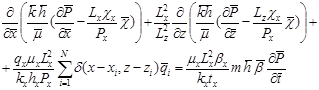. (4)
Введем обозначения:
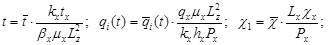
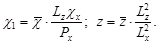
Запишем уравнений в безразмерном виде и для удобства записи безразмерных задач опустим черточки, таким образом уравнения (4) примет вид (1).
Таким образом, двумерную задачу (1) — (3) решим методом переменных направлений с точностью аппроксимации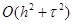 
.
Уравнение (1) можно записать в виде:
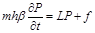, (5)
где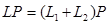 
; 
, 
,
.
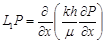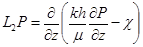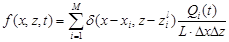Далее введем промежуточные значения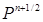 
, которые можно формально рассматривать как значение давления на дробном временном шаге при 
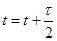. Переход от слоя n к слою n+1 совершается в два этапа:
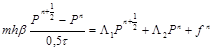, (6)
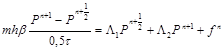; (7)
здесь L1, L2 — разностный аналог операторов L1, L2:
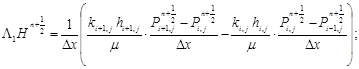(8)
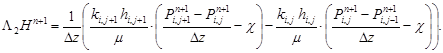(9)
Таким образом, решение краевой задачи (1)-(3) сведен к следующему алгоритму.
В начале находится значение давления на временном слое —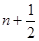 
. Для этого решается система (2.16) с соответствующими условиями методом потоковой прогонки для фиксированных j. затем используя полученные значения, решается система (9) с граничными условиями при фиксированных i и находят значения давления на полном временном слое — 
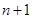во всех внутренних точках сеточной области.
Пусть, нагнетательные и эксплуатационные скважины установлены согласно рис.2.
Эксплуатационная скважина установлена в середине пласта по Х, а фильтр эксплуатационного скважина в глубине 15 м по разрезе Z.
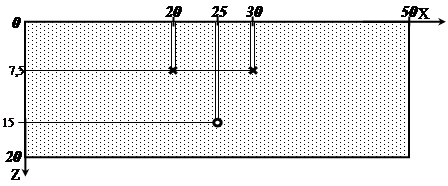
Рис.2. Схема расположения фильтра нагнетательных (х) и эксплуатационной (о) скважин
Основные гидрогеологические и геологические данные пласта приведены на табл. 1.
Таблица 1
Основные гидрогеологические и геологические данные
|
Ширина пласта (Х) |
50 м |
Мощность пласта (Z) |
20 м |
|
Коэффициент фильтрации пласта (K) |
5,8 м/сут |
Координаты фильтра нагнетательных и эксплуатационных скважин (xi, zi) |
1 — (20 м, 7,5 м) 2 — (25 м, 15 м) 3 — (30 м, 7,5 м) |
|
Удельный вес жидкости (c) |
0,91 г/см3 |
Дебиты скважин (qi) |
1–50 м3/сут 2 — -100 м3/сут 3–50 м3/сут |
Теоретические основы применения этажной системы ПВ, проверенные и подтвержденные практикой отработки этажных блоков и результатами анализов, предполагают постоянное гидродинамическое взаимодействие нагнетательных и эксплуатационных скважин от стадии подготовки запасов до полной их отработки. Поэтому рекомендуется отработку этажных блоков производить только в режиме одновременной закачки и откачки с соблюдением баланса растворов.
Проведенные на основе предложенной математической модели вычислительные эксперименты показали, что начальное давление пласта отличается от давления на эксплуатационной и нагнетательных скважинах. Начальное давление в зоне эксплуатационной скважины, в силу более глубокого расположения, будет больше чем на нагнетательных скважинах (рис. 3). однако с течением времени сначала они уравновешиваются, а потом давление в зоне эксплуатационной скважины, за счет отбора жидкости, уменьшается.
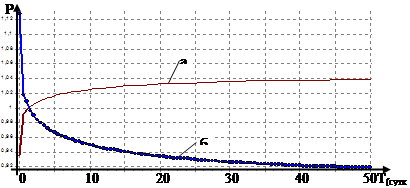
Рис. 3. Динамика изменения давления в нагнетательных (а) и эксплуатационной (б) скважинах при разном расположении скважин
Давление в зоне нагнетательной скважины увеличивается. И через несколько суток давления на скважинах стабилизуются и после этого распределение пластового давления не изменяется. Таким образом, из полученных результатов можно вытекает, что разработанная модель, учитывающая удельный вес выщелачивающего реагента, более адекватно описывает реальные условия, протекающие при разработке месторождений ПИ методом ПВ в условиях этажной системы разработки гидродинамические процессы, и ее можно применять при решении задач об управлении процессами ПВ в реальных условиях.
Литература:
1. Лукнер Л., Шестаков В. М. Моделирование миграции подземных вод. –М.: Недра, 1986. -208 с.
2. Самарский А. А. Введение в теорию разностных смех. –М.: Наука, 1971. –552 с.
3. Олимов М. Алгоритм решения прикладных задач для обыкновенных дифференциальных уравнений четвертого порядка с методом дифференциальной прогонки [Текст] / М. Олимов, О. О. Жакбаров, Ф. С. Ирискулов // Молодой ученый. — 2015. — № 6. — С. 193–196.
4. Жакбаров О. О. Создание пакета прикладных программ для оптимального управления процессом фильтрации для разработки газовых месторождений [Текст] / О. О. Жакбаров, Э. Д. Имамназаров, З. З. Кодиров // Молодой ученый. — 2015. — № 9. — С. 226–230.
