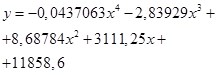Технологии Wolframalpha при изучении элементов прикладной математики студентами бакалавриата

Цель данной статьи — исследование дидактических возможностей WolframAlphaдля реализации метода наименьших квадратов (МНК, OLS, Ordinary Least Squares) — базового, доступного и широко применяемого метода регрессионного анализа. Данный метод, предложенный Карлом Фридрихом Гауссом и Адриеном Мари Лежандром, используется для оценки неизвестных параметров моделей аппроксимации (в том числе регрессионных моделей) по данным, имеющим различный содержательный смысл.

Введение. Необходимо отметить оправданную целесообразность изучения метода наименьших квадратов бакалаврами различных направлений подготовки. Благодаря своей относительной простоте и широте применения к различным ситуациям и проблемам он приобретает особую значимость для системы прикладной математической подготовки бакалавров в гуманитарном университете. Значимость прикладной математической подготовки бакалавров обусловлена с одной стороны возрастающими профессиональными требованиями (прикладная математика как основа естественно научных и гуманитарных исследований), с другой стороны математизацией и информатизацией всех сфер деятельности.

В рамках изучения МНКстудента бакалавриатаследует ознакомить с принципиальными возможностями и практикой исследования числовых характеристик и качественных свойств объектов в области будущей профессиональной деятельности, сведения прикладной задачи к изучению более простых, удобных объектов. Математическая ценность метода наименьших квадратов велика и заключается в приближённом представлении (аппроксимации) заданной функции другими (более простыми) функциями, в нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т. д. Прикладная ценность метода сводится к его широкому применению в нейронных сетях, в различных областях медицины, бизнеса, физике, геологии и технике, экономике, социологии, политологии для решения задач автоматизации, прогнозирования и классификации. Большую значимость МНК имеет в социально — экономической сфере: прогнозирование показателей в процессе исследования временных рядов. Данный метод, обеспечивающий аппроксимацию (приближение) имеет и научно — философское значение, заключающееся в замене одних объектов другими, с одной стороны более простыми, с другой в том или ином контексте близкими к исходным, называется аппроксимацией (приближением).

Рассмотрим идею и реализацию МНК в общем виде, доступном для восприятия студентами бакалавриата.

A.                      Постановка задачи.

Таблица 1

Вид экспериментальных данных для реализации МНК

Используя метод наименьших квадратов необходимо найти параметры линейной зависимости , выравнивающей данные (таблица 1).

B.                       Метод решения.

МНК предполагает минимизацию суммы квадратов отклонений от , т. е. задача сводится к  Другими словами при искомых значениях параметров а и bсумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. Найдем далее экстремум функции двух переменных, воспользовавшись необходимым условием экстремума

Относительно рассматриваемой функции по переменным а и b, получаем:

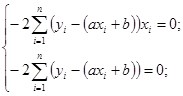
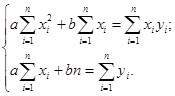
Решив данную систему двух уравнений с двумя переменными, получаем формулы для нахождения параметры линейной зависимости  по МНК:

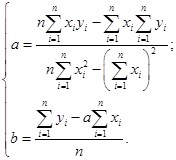
При данных а и b функция принимает наименьшее значение. Приведем доказательство этого утверждения.

Комментарий 1. Формула для нахождения параметра a содержит суммы, , , и параметр n — количество пар экспериментальных данных в таблице 1. Значения этих сумм можно рекомендовать вычислять отдельно. Коэффициент b следует находить после вычисления коэффициента a.

Доказательство. Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции  была положительно определенной. Покажем это.

Дифференциал второго порядка имеет вид:

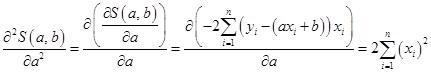
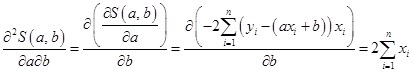
То есть

Следовательно, матрица квадратичной формы имеет вид

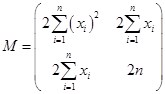 причем значения элементов не зависят от а и b.

Покажем, что найденная матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.

Угловой минор первого порядка

Неравенство строгое, так как точки несовпадающие. В дальнейшем это будем подразумевать.

Угловой минор второго порядка

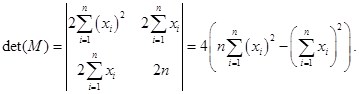
Докажем, что 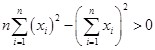 методом математической индукции.

1.                  База индукции. Проверим справедливость неравенства для любого значения n, например для n=2.

Получили верное неравенство для любых несовпадающих значений и .

2.                  Предположение. Предполагаем, что неравенство верное для n.

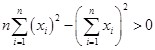 — верное.

3.                  Шаг индукции. Докажем, что неравенство верное для n+1.

То есть, нужно доказать, что 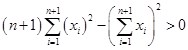 исходя из предположения что  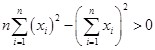— верное.

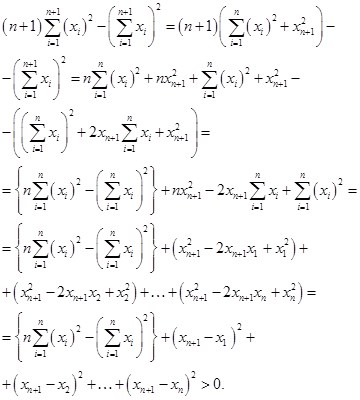
Выражение в фигурных скобках положительно по предположению индукции, а остальные слагаемые положительны, так как представляют собой квадраты чисел. Таким образом доказательство завершено.

Комментарий 2. Найденные значения а и bсоответствуют наименьшему значению функции , следовательно, являются искомыми параметрами для метода наименьших квадратов.

Комментарий 3. Вряде случаев возможно сведение аппроксимирующей функции, не являющейся многочленом, к многочлену с помощью замены переменной.

Таблица 2

Использование замены переменных при аппроксимации

№ п/п	Исходная функция	К какому виду приводится	Замена переменных
1.
2.
3.
4.
5.
6.
7.
8.

Остановимся далее на практических аспектах использованияWolframAlpha в учебном процессе (при изучении метода наименьших квадратов студентами бакалавриата) и представим результаты решения прикладной задачи. Во — перых, WolframAlpha предоставляет возможность строить графики функций по точкам, полученным, например, в результате эксперимента {,},{,},{,}. Во — вторых, для аппроксимации функции заданной таблично в WolframAlpha служит запрос fit, который использует метод наименьших квадратов. Различные варианты его использования приведем в таблице 3.

Таблица 3

Модели аппроксимации в WolframAlpha.

Название	Реализация
1.	Linear model Линейная аппроксимация	Linear fit {,},{,},{,}
2.	Quadratic model Квадратичная аппроксимация	quadratic fit{,},{,},{,}
3.	Cubic model Кубическая аппроксимация	cubic fit {,},{,},{,}
4.	Exponential model Экспоненциальная модель	exponential fit {,},{,},{,}
5.	Logarithmic model Логарифмическая модель	log fit {,},{,},{,}
6.	Polynomial model 4th order Полиномиальная аппроксимация 4-го порядка	polynomial of degree 4 fit {,},{,},{,}
7.	Polynomial model 10th order Полиномиальная аппроксимация 10-го порядка	polynomial of degree 10 fit {,},{,},{,}
8.	Choice by WolframAlpha Выбор WolframAlpha	Fit {,},{,},{,}

Прикладная задача. По данным сайта туристической биржи «БАНКО travel-inform» (http://www.tourdom.ru) «Средняя стоимость турпакета» и «Количество ночей в стране пребывания» распределены следующим образом (таблица 4). Найти зависимость между этими величинами с помощью метода наименьших квадратов.

Таблица 4

Данные прикладной задачи.

Воспользуемся возможностями WolframAlphaвизуализировать экспериментальные данные. Для построения корреляционного поля (первый этап исследования) представим экспериментальные данные таблицы 4 в специальном виде {1,15200}, {2,17000}, {3,22300}, {4,25000}, {5,26500}, {6,30000}, {7,31000}, {8,37400}, {9,39600}, {10,40000}, {11,41400}, {12,45300}. Анализ корреляционного поля позволяет во-первых, судить о наличии или отсутствии зависимости между величинами, во-вторых предположить вид искомой зависимости.

На втором этапе исследования, построив корреляционное поле (рисунок 1) необходимо поставить вопрос о выборе вида модели. Этот выбор в WolframAlphaреализован с помощью различных операторов, представленных в таблице 3.

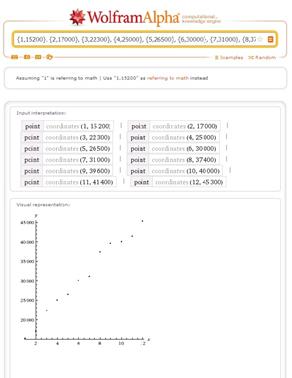
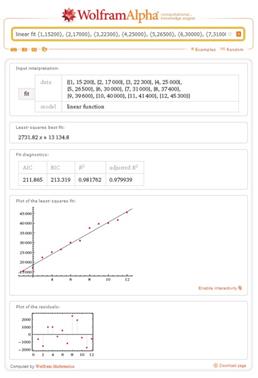
Рис. 1. Корреляционное поле          Рис. 2. Линейная модель

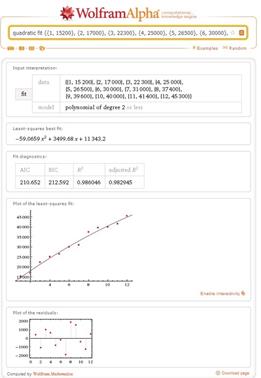
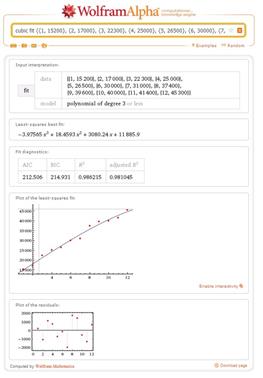
Рис. 3. Квадратичная модель.        Рис. 4. Кубическая модель

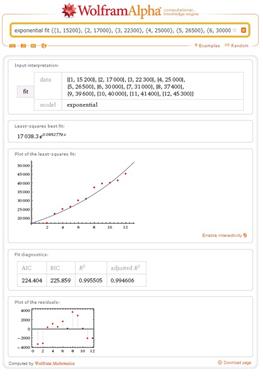
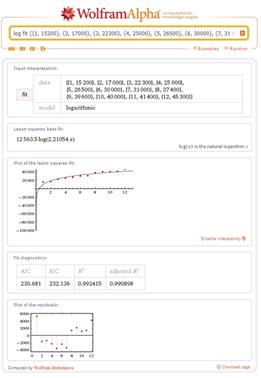
Рис. 5. Экспоненциальная модель  Рис. 6. Логарифмическая модель

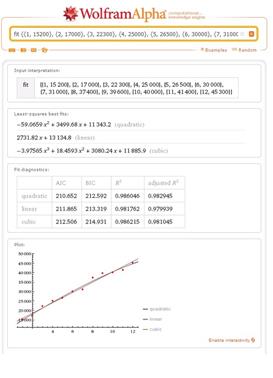
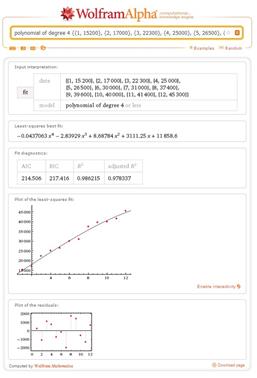
Рис. 7. Автоматический выбор     Рис. 8. Полиномиальная модель 4-ой степени

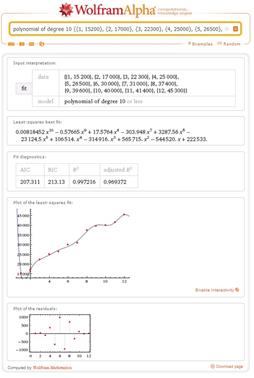
Рис. 9. Полиномиальная модель 10-ой степени

В таблице 5 представим основные результаты исследования прикладной задачи.

Таблица 5

Результаты аппроксимации в WolframAlpha.

Вид модели	Аналитический вид зависимости	Коэф-т детерми-нации	Скорректированный коэф-т детерми-нации adjusted
1.	Linear model Линейная аппроксимация
2.	Quadratic model Квадратичная аппроксимация
3.	Cubic model Кубическая аппроксимация
4.	Exponential model Экспоненциальная модель
5.	Logarithmic model Логарифмическая модель
6.	Polynomial model 4th order Полиномиальная аппроксимация 4-го порядка

Комментарий 4. Использование WolframAlpha позволяет не только получить аналитический вид зависимости, но и провести ее анализ, в частности найти коэффициент детерминации, и скорректированный коэффициент детерминации (в котором используются несмещённые оценки дисперсий). Отметим, что коэффициент детерминации для рассматриваемых моделей может принимать значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее исследуемая зависимость. При оценке регрессионных моделей это следует интерпретировать как соответствие построенной модели экспериментальным данным.

Литература:

1.         Pietro Balestra On the Efficiency of Ordinary Least-Squares in Regression Models. Journal of the American Statistical Association Vol. 65, No. 331 (Sep., 1970), pp. 1330–1337

2.         Orlando Gomes Ordinary least squares learning and nonlinearities in macroeconomics. Journal of Economic Surveys, Volume 24, Issue 1, pages 52–84, February 2010

3.         Власов Д. А., Синчуков А. В., Качалова Г. А. Количественные методы и математическое моделирование. — М.: Типография «11 формат», 2012. — 80 с.

4.         Власов Д. А., Синчуков А. В. Стратегия развития методической системы математической подготовки бакалавров. // Наука и школа, № 5, 2012, С. 61–65.