При разработке тренажных и обучающих комплексов для подготовки операторов мобильных систем одной из актуальных задач является кусочно-линейная аппроксимация таблично-заданной функции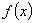 
системой функций 
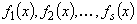из условий максимальной длительности интервалов аппроксимации и при совпадении узлов аппроксимации. Наличие двух критериев порождает неоднозначность в постановке задачи: возможны вариации в алгоритме, не влияющие на решение поставленной задачи.
Приведем алгоритм аппроксимации, который использовался при разработке имитатора динамики полета тренажера транспортного самолета [1…4].
Блок ввода данных. Вводятся: функция 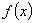, интервал 
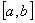, относительная погрешность аппроксимации 
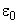в %.
Функция 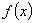реализуется в виде программы, позволяющей вычислить ее значение в любой точке 
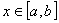или, хотя бы, в точках 
(
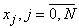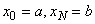), расположенных достаточно плотно:
, 
.
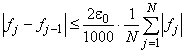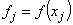При реализации программы используются:
- таблица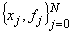 
,
- число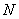 
точек табулирования,
- абсолютная погрешность аппроксимации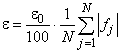 
; принималось 
.
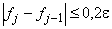Блок табулирования. Блок можно организовать различными способами с учетом имеющейся и дополнительной информации о функции 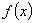(если таковая имеется).
Алгоритм включает вычисление
; 
;
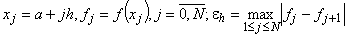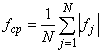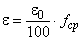
при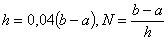 
.
Если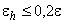 
, то необходимая информация получена. Если же 
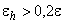, то, уменьшается 
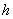в два раза и продолжаются указанные вычисления (
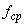и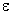 
можно не вычислять, они уже получены с достаточной точностью). Для сокращения вычислений таблицу 
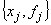следует лишь дополнить отсутствующими значениями.
Блок кусочно-линейной аппроксимации. Кусочно-линейная аппроксимация функции 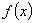(обозначается 
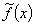) определяется таблицей 
(
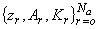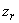- узлы аппроксимации, 
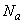- число узлов; 
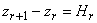- интервалы аппроксимации, 
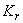- угловые коэффициенты). Справедливо:
;
;
; 
.
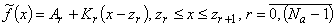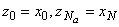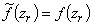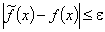
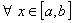В силу непрерывности 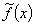имеем:
.
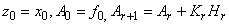Таким образом, для кусочно-линейной аппроксимации достаточно вычисления для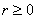 
значений 
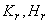(параметры 
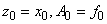уже определены при табулировании функции 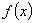в предыдущем блоке). Для удобства пользования значения 
; 
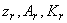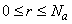сохраняются в памяти ЭВМ.
Максимальность интервалов аппроксимации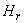 
следует из используемого ниже алгоритма, где точка 
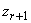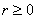, определяется как максимально удаленная от 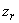(считая, что 
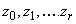уже вычислены). Предполагается:
; , 
.
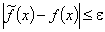
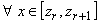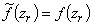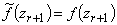Алгоритм вычисления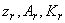 
. Полагая 
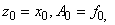по значениям 
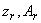вычисляются значения 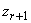, а затем 
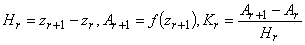. Точка 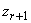будет одной из точек 
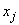(точек табулирования).
Алгоритм вычисления .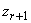
1. Для точки табулирования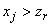 
проверяется условие
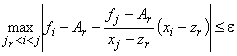, (1)
где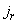 
- номер точки табулирования 
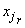, соответствующей (
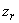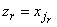). Переход к п.2.
2. Как только условие при некотором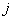 
нарушается, то 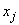запоминается как 
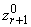; номер 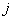запоминается как 
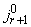; принимается 
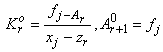. Переход к п.3.
3. Проверяется условие (1) для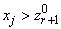 
.
3.1. Если условие (1) для всех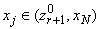 
не выполняется, то принимается 
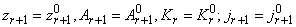(весь интервал 
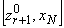оказывается «интервалом запрета»). Осуществляется переход к вычислению 
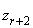(принимается 
).
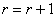3.2. Если условие (1) для некоторого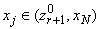 выполняется (пройден «интервал запрета»), то переход к п.1. (
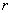не увеличивается).
Так будут определены все тройки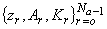 
. В последней тройке 
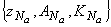достаточно вычислить лишь 
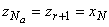и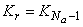 
.
Если при выполнении условия (1) при некотором 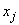окажется, ч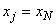то 
, то
; 
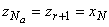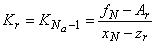. Завершение вычислений.
Замечание. Если функция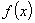 
удовлетворяет условию 
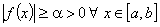, то вместо условия (1) можно использовать условие 
.
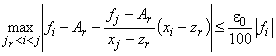Однако «трубка погрешности» при этом будет слишком неравномерной, отрицательно влияет на результат, если только задача не связана с некоторыми сингулярностями функции 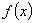в окрестности нулей.
Предлагаемый алгоритм эффективно использовался при разработке комплексов для подготовки операторов и других мобильных систем [5…8].
Литература:
1. Лапшин Э. В., Данилов А. М., Гарькина И. А., Клюев Б. В., Юрков Н. К. Авиационные тренажеры модульной архитектуры: монография. — Пенза, ИИЦ ПГУ. — 2005. –146 с.
2. Гарькина И. А., Данилов А. М. Аппроксимационные задачи при разработке имитаторов транспортных систем: распараллеливание вычислительных процессов / Вестник Таджикского технического университета. -№ 4 (24). — 2013.С.75–80.
3. Гарькина И. А., Данилов А. М., Петренко В. О. Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. № 2(41). 2013. –С.123–130.
4. Будылина Е. А.,Гарькина И. А., Данилов А. М. Приближенные методы декомпозиции при настройке имитаторов динамических / Региональная архитектура и строительство. № 3(17). 2013. — C. 150–156.
5. Будылина Е. А., Гарькина И. А., Данилов А. М., Махонин А. С. Основные принципы проектирования сложных технических систем в приложениях / «Молодой ученый. — № 5(52), Том 1, 2013. — с.39–42.
6. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы проектирования / Региональная архитектура и строительство. — 2012. — № 1. — С. 39–42.
7. Планирование эксперимента. Обработка опытных данных монография / И. А. Гарькина [и др.]; под ред. проф. А. М. Данилова.– М.: Палеотип, 2005. — 272 с.
8. Гарькина И. А., Данилов А. М., ЛапшинЭ.В., Юрков Н. К. Системные методологии, идентификация систем и теория управления: промышленные и аэрокосмические приложения / Известия высших учебных заведений. Поволжский регион. Технические науки. — 2009. — № 1(9). — С.3–11.
