Библиографическое описание:
Ганиев, М. М. Модель Фридрихса и ее спектр / М. М. Ганиев. — Текст : непосредственный // Молодой ученый. — 2017. — № 5 (139). — С. 551-553. — URL: https://moluch.ru/archive/139/38634/ (дата обращения: 26.04.2024).
Как известно, некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектра модели Фридрихса [1–3].
Введем оператор 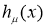 модели Фридрихса, действующий в
модели Фридрихса, действующий в 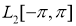 , как
, как
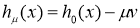 ,
,
где операторы 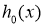 и
и 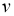 определяются по правилам
определяются по правилам
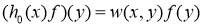 ,
,
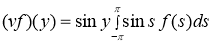 .
.
Здесь 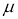 –положительное действительное число, а функция
–положительное действительное число, а функция 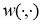 имеет вид
имеет вид
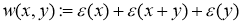 ,
,
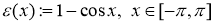 .
.
При этих предположениях оператор
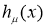
является ограниченным и самосопряженным в
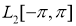
.
В настоящей работе изучаем некоторые спектральные свойства модели Фридрихса 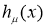 .
.
Возмущение 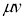 оператора
оператора 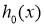 является самосопряженным одномерным оператором. Из известной теоремы Вейля [4] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр
является самосопряженным одномерным оператором. Из известной теоремы Вейля [4] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр 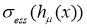 оператора
оператора 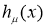 совпадает с существенным спектром оператора
совпадает с существенным спектром оператора 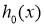 . Известно, что
. Известно, что
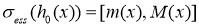 ,
,
где числа 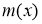 и
и 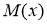 определяются равенствами
определяются равенствами
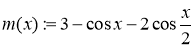 ,
,
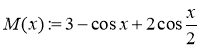 .
.
Следовательно,
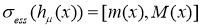 .
.
Пусть 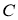 –комплексная плоскость. Для любого
–комплексная плоскость. Для любого 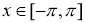 определим аналитическую функцию
определим аналитическую функцию 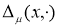 (детерминант Фредгольма, ассоциированный с оператором
(детерминант Фредгольма, ассоциированный с оператором 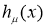 ):
):
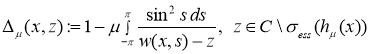 .
.
Теперь установим связь между собственными значениями оператора
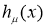
и нулями функции
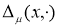
.
Теорема 1. При каждом фиксированном 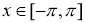 оператор
оператор 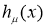 имеет собственное значение
имеет собственное значение 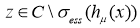 тогда и только тогда, когда
тогда и только тогда, когда 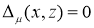 .
.
Доказательство. Пусть число 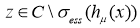 есть собственное значение оператора
есть собственное значение оператора 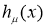 , а
, а 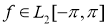 –соответствующая собственная функция. Тогда функция
–соответствующая собственная функция. Тогда функция 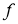 удовлетворяет уравнению
удовлетворяет уравнению
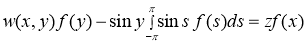 . (1)
. (1)
Заметим, что для любых 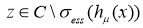 и
и 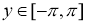 имеет место соотношение
имеет место соотношение 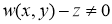 . Тогда из уравнения (1) для
. Тогда из уравнения (1) для 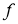 имеем
имеем
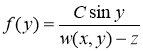 , (2)
, (2)
где
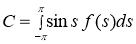 . (3)
. (3)
Подставляя выражение (2) для 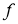 в равенства (3), получим, что уравнение (1) имеет ненулевое решение тогда и только тогда, когда
в равенства (3), получим, что уравнение (1) имеет ненулевое решение тогда и только тогда, когда
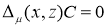 ,
,
т. е. когда
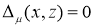
.
Теорема 1 доказана.
Из теоремы 1 вытекает следующее:
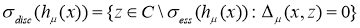 .
.
Из определения функции 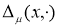 видно, что при всех
видно, что при всех 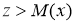 имеет место неравенство
имеет место неравенство 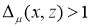 . В силу теоремы 1 это означает, что для любого
. В силу теоремы 1 это означает, что для любого 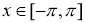 оператор
оператор 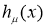 не имеет собственных значений в интервале
не имеет собственных значений в интервале 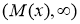 . Из монотонности функции
. Из монотонности функции 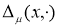 в интервале
в интервале 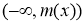 имеем, что для любого
имеем, что для любого 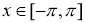 оператор
оператор 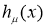 имеет не более одного собственного значения в интервале
имеет не более одного собственного значения в интервале 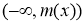 . Если
. Если 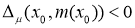 при некотором
при некотором 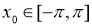 , то оператор
, то оператор 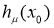 имеет единственное простое собственное значение в интервале
имеет единственное простое собственное значение в интервале 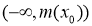 .
.
Литература:
-
Л. Д. Фаддеев. О модели Фридрихса в теории возмущений непрерывного спектра. Труды мат. инс-та АН СССР, Т. 73, М.: Наука, 1964, С. 292–313.
-
Р. А. Минлос, Я. Г. Синай. Исследование спектров стохастических операторов, возникающих в решетчатых моделях газа. ТМФ, 1979, Т. 2, № 2. С. 230–243.
-
Е. М. Дынкин, С. Н. Набако, С. И. Яковлев. Границы конечности сингулярного спектра в самосопряженной модели Фридрихса. Алгебра и анализ. Т. 3, № 2, 1991, С. 77–90.
-
М.Рид, Б.Саймон. Методы современной математической физики. Т.4. Анализ операторов. М.: Мир, 1982.
Основные термины (генерируются автоматически): оператор, собственное значение, собственное значение оператора, существенный спектр оператора.
Похожие статьи
Описывается его существенный и дискретный спектры. Найдены условия существования собственных значений.
Пусть число — есть собственное значение оператора и пусть — соответствующая собственная вектор-функция.
Обозначим через и , соответственно, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Теорема 2. Если один из операторов или имеет собственное значение тогда оператор имеет единственное простое собственное значение на.
При этом нуль является нижней гранью существенного спектра оператора .
Лемма 1. Оператор имеет собственное значение тогда и только тогда, когда . Из леммы 1 вытекает, что , где.
Получен аналог уравнения Вайнберга для собственных функций оператора . Ключевые слова: модельный оператор, нелокальный потенциал, уравнение Вайнберга, собственное значение и собственная функция, существенный спектр.
Обозначим через и соответственно существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Следующая лемма устанавливает связь между собственными значениями оператора и нулями функции .
При этом нуль является нижней гранью существенного спектра оператора .
В ходе доказательства теоремы 1 показали, что если оператор имеет нулевое собственное значение, вектор–функция , где , а определен по формуле (2), удовлетворяет уравнению и .
Описывается множества собственных значений этого оператора и задача состоит в обосновании этих описаний.
сохранении существенного спектра при возмущениях конечнего ранга вытекает, что существенный спектр оператора совпадает с существенным спектром...
Обозначим через и , соответственно, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Теорема 1. Число является собственным значением оператора тогда и только тогда, когда .
Множество называется существенным спектром оператора .
Оператор , имеет единственное простое собственное значение равное . Теперь сформулируем основной результат работы.
В работе доказано, что существенный спектр трехчастичного дискретного оператора Шредингера состоит из объединения не
в том случае, когда соответствующий двухчастичный дискретный оператор Шредингера имеет бесконечное число собственных значений.
Описывается его существенный и дискретный спектры. Найдены условия существования собственных значений.
Пусть число — есть собственное значение оператора и пусть — соответствующая собственная вектор-функция.
Обозначим через и , соответственно, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Теорема 2. Если один из операторов или имеет собственное значение тогда оператор имеет единственное простое собственное значение на.
При этом нуль является нижней гранью существенного спектра оператора .
Лемма 1. Оператор имеет собственное значение тогда и только тогда, когда . Из леммы 1 вытекает, что , где.
Получен аналог уравнения Вайнберга для собственных функций оператора . Ключевые слова: модельный оператор, нелокальный потенциал, уравнение Вайнберга, собственное значение и собственная функция, существенный спектр.
Обозначим через и соответственно существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Следующая лемма устанавливает связь между собственными значениями оператора и нулями функции .
При этом нуль является нижней гранью существенного спектра оператора .
В ходе доказательства теоремы 1 показали, что если оператор имеет нулевое собственное значение, вектор–функция , где , а определен по формуле (2), удовлетворяет уравнению и .
Описывается множества собственных значений этого оператора и задача состоит в обосновании этих описаний.
сохранении существенного спектра при возмущениях конечнего ранга вытекает, что существенный спектр оператора совпадает с существенным спектром...
Обозначим через и , соответственно, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Теорема 1. Число является собственным значением оператора тогда и только тогда, когда .
Множество называется существенным спектром оператора .
Оператор , имеет единственное простое собственное значение равное . Теперь сформулируем основной результат работы.
В работе доказано, что существенный спектр трехчастичного дискретного оператора Шредингера состоит из объединения не
в том случае, когда соответствующий двухчастичный дискретный оператор Шредингера имеет бесконечное число собственных значений.
![]() модели Фридрихса, действующий в
модели Фридрихса, действующий в ![]() , как
, как
![]() ,
,
![]() и
и ![]() определяются по правилам
определяются по правилам
![]() ,
,
![]() .
.
![]() –положительное действительное число, а функция
–положительное действительное число, а функция ![]() имеет вид
имеет вид
![]() ,
,
![]() .
.
![]() .
.
![]() оператора
оператора ![]() является самосопряженным одномерным оператором. Из известной теоремы Вейля [4] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр
является самосопряженным одномерным оператором. Из известной теоремы Вейля [4] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр ![]() оператора
оператора ![]() совпадает с существенным спектром оператора
совпадает с существенным спектром оператора ![]() . Известно, что
. Известно, что
![]() ,
,
![]() и
и ![]() определяются равенствами
определяются равенствами
![]() ,
,
![]() .
.
![]() .
.
![]() –комплексная плоскость. Для любого
–комплексная плоскость. Для любого ![]() определим аналитическую функцию
определим аналитическую функцию ![]() (детерминант Фредгольма, ассоциированный с оператором
(детерминант Фредгольма, ассоциированный с оператором ![]() ):
):
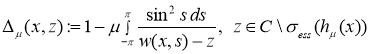 .
.
![]() оператор
оператор ![]() имеет собственное значение
имеет собственное значение ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
![]() есть собственное значение оператора
есть собственное значение оператора ![]() , а
, а ![]() –соответствующая собственная функция. Тогда функция
–соответствующая собственная функция. Тогда функция ![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() . (1)
. (1)
![]() и
и ![]() имеет место соотношение
имеет место соотношение ![]() . Тогда из уравнения (1) для
. Тогда из уравнения (1) для ![]() имеем
имеем
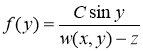 , (2)
, (2)
![]() . (3)
. (3)
![]() в равенства (3), получим, что уравнение (1) имеет ненулевое решение тогда и только тогда, когда
в равенства (3), получим, что уравнение (1) имеет ненулевое решение тогда и только тогда, когда
![]() ,
,
![]() .
.
![]() видно, что при всех
видно, что при всех ![]() имеет место неравенство
имеет место неравенство ![]() . В силу теоремы 1 это означает, что для любого
. В силу теоремы 1 это означает, что для любого ![]() оператор
оператор ![]() не имеет собственных значений в интервале
не имеет собственных значений в интервале ![]() . Из монотонности функции
. Из монотонности функции ![]() в интервале
в интервале ![]() имеем, что для любого
имеем, что для любого ![]() оператор
оператор ![]() имеет не более одного собственного значения в интервале
имеет не более одного собственного значения в интервале ![]() . Если
. Если ![]() при некотором
при некотором ![]() , то оператор
, то оператор ![]() имеет единственное простое собственное значение в интервале
имеет единственное простое собственное значение в интервале ![]() .
.







