1. Алгоритмы

Развитие рынка мобильных гаджетов привело к тому, что на сегодняшний день жизнь практически каждого человека связана с этими устройствами.

Большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.

Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат.

Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели.

Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом.

Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно.

Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение.

Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма.

Алгоритмы применяются во всех направлениях IT и во многих других отраслях.

Далее мне предстояло погрузиться в мир мобильной разработки.

2. Операционная система Андроид.

2.1. Почему Андроид?

В настоящий момент существует несколько популярных мобильных операционных систем.

Основной выбор был между этими двумя системами.

– больший охват пользователей и количество устройств в мире;

– помимо мобильных телефонов на операционной системе Андроид работают телевизоры, мультимедиа системы в автомобилях, носимая электроника, планшеты, электронные книги и даже ноутбук;

– для разработки не требуется ноутбук или компьютер компании Apple.

– большое комьюнити разработчиков, много прикладных библиотек, инструментов разработки и источников информации;

– доступность и разнообразие мобильных телефонов.

Также для распространения приложения на базе операционной системы Андроид не требуется оплата ежегодного взноса.

Эти преимущества стали причиной выбора Андроид.

3. Инструменты для разработки мобильного приложения.

В качестве платформы для разработки приложения была выбрана операционная система Андроид.

Компания Google предоставляет широкий набор инструментов разработки.

Помимо Android Studio ключевым элементом является Android SDK.

Текущий версия SDK имеет номер 13 или API 33 (Application Programming Interface — описание способов взаимодействия одной компьютерной программы с другими).

Также не обойтись без эмулятора для отладки приложения и ряда плагинов.

Мной была настроена среда разработки, установленные необходимые плагины, sdk и эмулятор.

4. Пользовательский интерфейс.

4.1. Выбор подхода в реализации пользовательского интерфейса.

Выбор стоял между привычным в андроид среде императивными фреймворками и декларативным подходом.

Декларативное программирование — это парадигма, которая позволяет нам задавать программы, не описывая control flow.

Этот пример не про UI, но позволяет объяснить разницу на реальном коде.

Пожалуй, главным трендом мобильной разработки за последние несколько лет стал декларативный UI.

Официальная история Jetpack Compose начинается с мая 2019, когда он был представлен публике на конференции Google I/O.

4.2. Какие же преимущества у декларативного подхода?

Итак, чем же хорош Jetpack Compose и, главное, чем он кардинально отличается от существующего на данный момент UI-фреймворка Android?

– Jetpack Compose не зависит от конкретных релизов платформы, а значит, не нужно использовать Support Library.

– Больше не нужно переключаться между классами и xml-файлами — вся работа с UI происходит в одном Kotlin-файле.

– Каждый UI-компонент представляет собой обычную composable-функцию, отвечающую только за ограниченный функционал, т. е.

– Одна из основополагающих концепций Jetpack Compose это движение данных в одном направлении.

– Обратная совместимость: для использования Compose не требуется начинать проект с нуля.

– Меньше кода: тут, как говорится, «лучше один раз увидеть, чем сто раз услышать».

5. Язык программирования Kotlin.

Современный, лаконичный и безопасный язык разработки от компании JetBrains, работающий поверх Java Virtual Machine (JVM).

Это статически-типизированный, объектно-ориентированный язык программирования.

Объектно-ориентированными называют языки, в которых все операции происходят с объектами — блоками кода, куда можно «складывать» несколько значений.

Статическая типизация означает, что типы переменных задаются разработчиком до выполнения программы.

В отличие от своего предшественника, Java, Kotlin более безопасен.

Kotlin полностью совместим с Java.

В 2017 году на Google I/O анонсировали поддержку языка Kotlin для разработки приложений под Android с помощью IDE Android Studio.

Согласно статистике Google (I/O 2021), Kotlin сейчас и самый популярный язык разработки под Android.

Потенциально Kotlin можно использовать везде, где работает Java — а это и бэкенд, и веб, и десктоп, и куча других задач.

Тем не менее у каждого языка есть своя ниша — та сфера, где его используют больше всего программистов.

6. Пять в ряд или крестики нолики без границ.

В рамках проекта необходимо разработать мобильную игру в «крестики-нолики» или «пять в ряд» с реализацией пользовательского интерфейса на языке высокого уровня и с использованием объектно-ориентированного подхода.

А «пять в ряд» — это естественное развитие обычных «крестиков-ноликов».

– Игровое поле теперь «бесконечное», то есть ограниченное только размерами листа бумаги (а не 3×3, как в обычных «крестиках-ноликах»);

– Для победы нужно выстроить ряд из пяти крестиков или ноликов по горизонтали, вертикали или диагонали (а не три, как в обычных «крестиках-ноликах»).

Обычно договариваются также, что ряд из шести (или большего количества) крестиков или ноликов также обеспечивает победу своему игроку.

Зачем вообще нужно было как-то развивать обычные «крестики-нолики»?

Игра до 4 одинаковых знаков на бесконечном поле неинтересна, ибо начинающий довольно быстро строит «вилку» и выигрывает.

Прародителем игры являются логическая игра головоломка, имеющая японское название «Гомоку» или китайское «Рэндзю».

6.1. Как определить конец игры, победу одного из игроков?

Изначально мною был выбран самый простой алгоритм.

На рисунке приведен пример победного хода ноликом.

Для упрощения реализации игрового поля мною было сделано допущение, что оно будет иметь ограниченный размер, который можно будет задавать в приложении.

Но это же упрощение навело меня на мысль, что можно упростить алгоритм определения победного хода в игре.

Я так и сделал.

6.2. А что, если, заполнив все игровые клетки никто так и не сможет выиграть?

Для обычной игры 5 в ряд такой вариант обычно невозможен, так как поле не имеет границ.

Такая ситуация в играх называется Ничьей.

Возможно 2 варианта реализации определения ничьи. Первый — это проверка всех игровых клеток на наличие свободной.

На рисунке можно увидеть вариант игры завершившейся в ничью.

7. Выбор алгоритма

Научившись определять разные состояния игры можно приступить к выбору алгоритма выбора хода-кандидата.

Немного информации о том, что такое игра гомоку.

Гомоку (яп. «пять пунктов») или, как его иногда называют, «гомоку-нарабэ» (五目並べ, «пять пунктов в ряд») — настольная логическая игра для двух игроков. На квадратной доске размером 19×19 (в традиционном варианте) или 15×15 (в современном спортивном варианте) пунктов игроки поочерёдно выставляют камни двух цветов. Выигрывает тот, кто первым построит непрерывный ряд из пяти камней своего цвета по вертикали, горизонтали или диагонали.

7.1. Вариант № 1: перебор в лоб

Идея состоит в том, что у нас нет никакой функции оценки, никакой эвристики. Мы просто расставляем элементы на поле, пока не достигнем пяти одинаковых крестиков или ноликов подряд в линию.

7.2. Вариант № 2: альфа-бета отсечение

Альфа-бета отсечение — алгоритм поиска, стремящийся сократить количество узлов, оцениваемых в дереве поиска алгоритмом минимакса.

Минимакс — правило принятия решений, для минимизации возможных потерь из тех, которые нельзя предотвратить при развитии событий по наихудшему сценарию.

Антагонистическая игра или игра с нулевой суммой — термин теории игр.

В основе алгоритма лежит идея, что оценивание ветви дерева поиска может быть досрочно прекращено (без вычисления всех значений), если было найдено, что для этой ветви значение оценивающей функции в любом случае хуже, чем вычисленное для предыдущей ветви.

Попробуем использовать функцию оценки в качестве критерия выбора хода.

Этот вариант нам не подходит.

Пример, алгоритма альфа-бета отсечение приведен на рис 1.

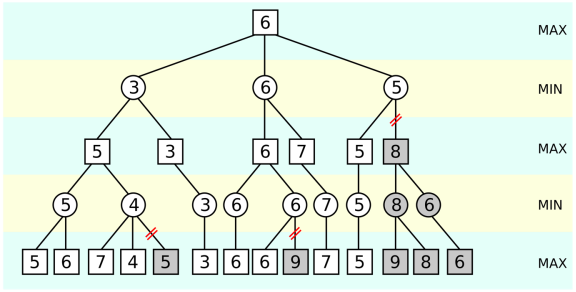
Рис. 1. Алгоритм альфа-бета отсечение

7.3. Вариант № 3: решение с конца

Идея состоит в том, чтобы распознавать шаблоны, которые ведут к победе.

Игра всегда заканчивается линией из 5 элементов. Если мы вернёмся на шаг назад, получим предыдущие комбинации.

Но есть проблема — большое число комбинаций, которое нужно хранить в памяти.

7.4. Mr. Allis доказал, что крестики всегда побеждают

В 1992 году мистер Алис (Allis), используя 10 рабочих станций SUN SPARC, доказал для классического гомоку с полем 15х15, что крестики всегда побеждают. Станции имели 64 и 128MB RAM.

Это важная информация для понимания теории, но на практике же мы реализуем свой алгоритм, который не потребует таких вычислительных мощностей.

7.5. Вариант № 4: оценочная функция

Скорость поиска очень чувствительна к порядку обхода.

Для рассуждения и оценки введем некоторые понятия для простоты рассуждения в дальнейшем.

Данный вариант наиболее прост в реализации и позволит итерационно улучшать сложность алгоритма разбирая и учитывая возможные комбинации.

8. Выбранный алгоритм

В качестве алгоритма для игры пять в ряд был выбран вариант оценочной функции.

Он наиболее прост в реализации и при этом показал неплохой уровень игры с человеком.

Реализуя данный алгоритм, я прошел через несколько этапов его совершенствования и в мобильном приложении это стало вариантами выбора сложности от легкого к среднему и далее сложному.

Но для начала немного поговорим о возможных комбинациях в игре и их ценности для определения наиболее выгодного хода.

Рассмотрим рисунок с тройными комбинациями на рис2.

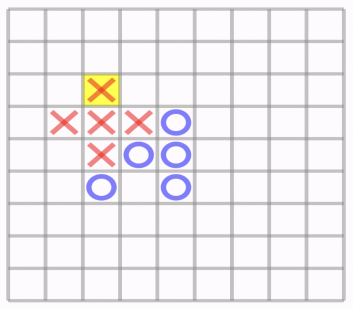
Рис. 2. Рисунок с тройными комбинациями

Открытая тройка.

Открытая тройка 2х.

Атакующий ход имеет больший вес, чем аналогичный ход защиты.

По аналогии можно описать и другие комбинации с двойками и единицами.

8.1. Легкая сложность

Для упрощения этой операции я решил придумать формулу вычисление веса текущей клетки.

Из описанных ранее комбинаций можно увидеть, что единственным ходом, гарантирующим победу, является закрытие своей четверки пятым крестиком или ноликом.

Примем, для удобства рассуждений, что мы (компьютер, наш алгоритм) играем крестиками, а человек (соперник) играет ноликами.

Будем рассчитывать количество подряд идущих крестиков или ноликов в строке и складывать их значение до пустой клетки, границ нашей доски или знака соперника. Для четверки сумма будет равна 4.

Вес клетки = 10 * количество подряд идущих знаков * 2 (если это наши знаки, т. е.

Четверка наших крестиков будет иметь вес 10 * 4 * 2 = 80, а четверка ноликов — 10 * 4 = 40.

Тройка наших крестиков будет иметь вес 10 * 3 * 2 = 60, а четверка ноликов — 10 * 3 = 30.

С этим алгоритмом уже вполне можно играть с компьютером.

В нашем расчете можно заметить, что вес нашей тройки больше, чем вес четверки соперника.

Очевидно, что текущий результат нас не может устроить и наш алгоритм нужно совершенствовать далее.

8.2. Средняя сложность

Нам нужно улучшить работу нашего алгоритма и для начала исправить проблему, что вес нашей тройки больше веса четверки соперника.

Как нам этого добиться?

Наша задача сделать так, чтобы вес четверок был на порядок больше веса тройки и всегда «побеждал» при подсчете.

Степень числа — это результат многократного умножения числа на себя, что показано на рис 3.

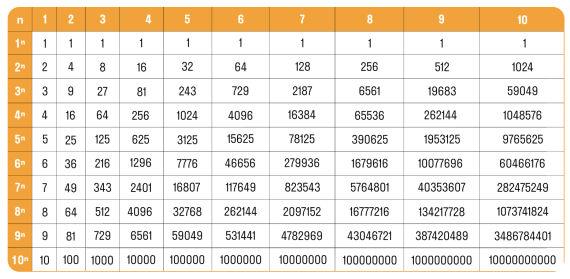
Рис. 3 Многократное умножение

Можно выбрать любую степень, главное, чтобы ее основание было достаточно большим.

Моя формула приобрела следующий вид:

Вес клетки = (10 ^ количество подряд идущих знаков) * 2 (если это наши знаки, т. е.

Проверим нашу формулу на расчете веса четверки и тройки.

Четверка наших крестиков будет иметь вес 2 * 10 ^ 4 = 20 000, а четверка ноликов — 10 ^ 4 = 10 000.

Тройка наших крестиков будет иметь вес 2 * 10 ^ 3 = 2 000, а четверка ноликов — 10 ^ 3 = 1 000.

Проверяем на наличие недостатка из прошлой формулы.

Данная реализация алгоритма играет намного интереснее первого варианта и с ней уже можно посоревноваться.

Но все-таки она не лишена ряда недостатков.

Одним из таких является тот, что не учитывается в расчете веса факт того, что данная последовательность является открытой (нет ограничений с двух сторон и можно продолжить ставить знаки с любой стороны).

Например, закрытая тройка будет иметь тот же вес, что и открытая.

На рисунке можно увидеть, что закрытая тройка крестиков не имеет перспектив к победе в отличие от открытой тройки ноликов.

8.3. Тяжелая сложность

Для учета разницы между открытыми и закрытыми последовательностями нужно внести изменение в формулу расчет веса.

Как нам это сделать?

Одним из вариантов сразу пришедшим в голову было вычитание некоего веса из суммы закрытой последовательности, чтобы она была меньше открытой.

Путем экспериментов с изменением формулы я стал вычитать коэффициент из степени и тем самым влиять на вес:

Вес клетки = (10 ^ (количество подряд идущих знаков — количество ограничений последовательности)) * 2 (если это наши знаки, т. е.

Для понимания приведем пример:

– Старый вес закрытой тройки (_?xxx_) = 2 * 10 ^ 3 = 2000

– Новый вес закрытой тройки с одной стороны (_?xxxo) = 2 * 10 ^ (3–0.5) = 632

– Новый вес закрытой тройки с обоих сторон (o?xxxo) = 2 * 10 ^ (3–1) = 200

Поясним:

х — наш символ

o — символ соперника

_ — пустая клетка

Проверим на нашей формуле вес нашей закрытой с одной стороны четверки и открытой четверки соперника.

Наша закрытая четверка (_?ххххо): 2 * 10 ^ (4–0.5) = 6324

Открытая четверка соперника (_?оооо_): 10 ^ 4 = 10000

Мы видим, что новая формула неверно оценивает выгодность хода.

Наша закрытая четверка (_?ххххо): 4 * 10 ^ (4–0.5) = 12649

Открытая четверка соперника (_?оооо_): 10 ^ 4 = 10000

Итак, мы видим, что наша четверка вновь более предпочтительна при выборе хода.

Новая версия алгоритма уже может заставить попотеть начинающего игрока пять в ряд и осуществить немало интересных комбинаций на игровом поле.

Дальнейшие проверки, совершенствования и учет ключевых комбинаций могут улучшить алгоритм.

9. Разработка мобильного приложения

Выбрав в качестве платформы, для реализации алгоритма для игры пять в ряд, Андроид я осознавал стоящие передо мной сложности.

Первым делом я изучил материалы по первоначальной настройки среды разработки на сайте d.android.com.

Дополнительно я установил эмулятор и запустил конфигурацию с последней версией Android SDK API 33 для отладки приложения.

Пройдя несложный пошаговый onboarding я создал первый проект.

1. Что мне предстояло изучить для разработки мобильного приложения?

Передо мной стояли следующие задачи:

– Разобраться с архитектурой мобильного приложения андроид.

– Сконструировать пользовательский интерфейс

– Научится навигироваться между экранами и передавать информацию

– Реализовать алгоритм игры пять в ряд

– Опубликовать приложение в Google Play

2. Архитектура мобильного приложения андроид.

Архитектура Android приложений основана на идее многократного использования компонентов, которые являются основными строительными блоками.

Система Android выстроена таким образом, что любое приложение может запускать необходимый компонент другого приложения.

Когда система запускает компонент, она запускает процесс приложения, которому принадлежит компонент, если он еще не запущен, и создает экземпляры классов, необходимых компоненту.

Можно выделить четыре различных типа компонентов, каждый тип служит для достижения определенной цели и имеет свой особый жизненный цикл, который определяет способы создания и разрушения соответствующего компонента.

Активность (Activity) — это видимая часть приложения (экран, окно, форма), отвечает за отображение графического интерфейса пользователя. При этом приложение может иметь несколько активностей, например, в приложении, предназначенном для работы с электронной почтой, одна активность может использоваться для отображения списка новых писем, другая активность — для написания, и еще одна — для чтения писем.

Сервис (Service) — компонент, который работает в фоновом режиме, выполняет длительные по времени операции или работу для удаленных процессов.

Контент-провайдер (Content provider) управляет распределенным множеством данных приложения. Данные могут храниться в файловой системе, в базе данных SQLite, в сети, в любом другом доступном для приложения месте.

Приемник широковещательных сообщений (Broadcast Receiver) — компонент, который реагирует на широковещательные извещения. Большинство таких извещений порождаются системой, например, извещение о том, что экран отключился или низкий заряд батареи.

Мною был выбран подход при создании андроид приложения, когда используется только одна основная активность (Single Activity).

3. Пользовательский интерфейс.

Выбранный подход с единственной активностью позволил внедрить Jetpack Compose и декларативной стиль создания UI.

Поскольку Jetpack Compose применяет декларативный подход, то единственный способ обновить визуальный компонент представляет повторный вызов функции этого компонента, в которую передаются новые значения. И чтобы упростить обновление компонентов и вообще визуального интерфейса Jetpack Compose предоставляет концепцию состояние или state. Состояние представляет некоторое значение, которое хранится в приложении и которое в процессе его работы может изменяться.

Разберем реализацию первого экрана приложения (MainScreen). Этот экран отображается при старте приложения. Контент на экране помещается в контейнер Box.

Здесь есть два основных параметра:

– horizontalAlignment: Alignment.CenterHorizontal

– и verticalArrangement: Arrangement.Center.

Alignment.CenterHorizontal определяет выравнивание вложенных элементов по горизонтали.

VerticalArrangement определяет, как будут распределяться элементы по вертикали.

Рассмотрим код.

С помощью задания параметра fillMaxSize можно указать, что контейнер Box должен быть максимального размера и занять весь доступный экран.

Для понимания как элементы располагаются на экране обратим внимание на скриншот, изображенный на рис.4

Рис. 4. Крестики нолики

В первый контейнер Column входит ряд элементов.

Обратим внимание на элемент Button.

Принцип работы навигации будет освещен в следующем разделе.

Внизу экрана расположена второй контейнер Column с вертикально расположенными кнопкой «Выход» и номер версии приложения.

Рассмотрим функцию ExitButton на рис 5.

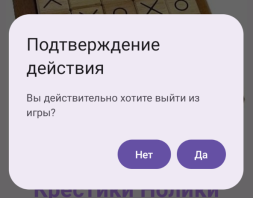
Рис. 5. ExitButton

В случае подтверждения выхода выполняется первое действие: переменная openExitDialog принимает значение false и отрисовка диалога более происходить не будет, а переменная exit = true инициализирует выполнение if (exit) и приводит к закрытию единственной активити, а значит и всей игры.

Начало реализации экрана и определение переменных для изменения отрисовки экрана.

Конец реализации экрана и применение переменных.

Аналогично реализованы все экраны приложения.

4. Навигация в приложении

Единственной точкой входа для приложения является функция, отвечающая за навигацию: Navigation().

Ее задача управлять переходом между экранами приложения и передавать параметры.

Возможны 4 экрана перехода:

Определим граф навигации, укажем название и стартовый экран startDestination (тип задаваемых значений String).

На следующем экране выбора крестика или нолика необходимо получить переданные параметр:

В качестве параметра указываем название экрана, тип и наименование передаваемого параметра.

Запускаем экран с выбором крестика или нолика (FigureScreen) и передаем в него выбранный ранее уровень сложности (level).

Аналогично поступаем и со следующим экраном.

На игровом экране значения используются для настройки сложности алгоритма и выбранного типа: крестик или нолик.

Навигация в приложении реализована.

Заключение

В ходе работы изучен процесс разработки мобильного приложения, реализован пользовательский интерфейс, использован язык программирования Kotlin и создан алгоритм игры «Пять в ряд».

Были решены следующие задачи:

– осуществлена постановка задачи, выделены требования к приложению;

– произведен выбор инструментов для реализации пользовательского интерфейса;

– изучены современные средства разработки мобильных приложений для Android;

– изучены теоретические основы языка программирования;

– реализован алгоритм для игры «Пять в ряд»

– определены требования и спроектировано мобильное приложение;

– реализовано, протестировано и опубликовано мобильное приложение.

Все поставленные задачи были решены, цель достигнута.

Литература:

1. Жемеров. Д, Исакова С. Kotlin в действии. ДМК Пресс, 2018. — 404с.
2. Аренс В. Математические игры. Центрполиграф, 2018. — 159с.
3. Гарднер М. Математические головоломки и развлечения. — МИР, 1999. — 512c.
4. Гарднер М. Лучшие математические игры и головоломки. — АСТ, 2009. — 256с.
5. Перельман Я. И. Занимательная математика. ТИОН, 2022. -144с.
6. Еленьский Щ. По следам Пифагора. Сто исторических головоломок. Качели, 2022. — 128c.