Введение

В настоящее время большое внимание в нашей стране уделяется подготовке инженеров [1]. В школах созданы инженерные классы. Автор работы решил применить разработанный им ранее аппаратно-программный микроконтроллерный комплекс для моделирования и экспериментального исследования модели в механике. Предложенные алгоритмы и экспериментальная установка могут использоваться при проведении факультативных занятий в инженерных классах, а также в курсе физики.

В работе решается задача применить разработанное автором работы микроконтроллерное устройство «Будущему инженеру» [2] для математического моделирования и экспериментального исследования физических процессов, модели которых обычно строятся с помощью методов высшей математики, недоступных школьнику

Используя компьютерное устройство, можно упростить решение физических задач, рассматривая описывающие их процессы в дискретные моменты времени и заменяя математические уравнения алгоритмами. Уменьшая промежутки между дискретными моментами времени, мы получим решение, соответствующее реальному миру. Это же устройство можно использовать для автоматизации физического эксперимента, подтверждающего результаты моделирования.

Принцип дискретизации физической модели использовался для компьютерного моделирования процесса посадки спускаемого аппарата на Луну [3]. Иные примеры такого подхода автор найти не смог. Рассматриваемая ниже задача о цепочке, точно решается только методами высшей математики [4].

Известны работы по автоматизации физического практикума на основе специализированных экспериментальных установок и готового программного обеспечения персонального компьютера (см., например, [5]). В частности, там предлагается использовать оптоэлектронный датчик для измерения промежутков времени. Преимуществом предлагаемого в настоящей работе решения является использование универсального микроконтроллерного устройства, которое легко подключается к оборудованию для эксперимента и программируется самим учеником.

Целью проекта является применение универсального микроконтроллерного устройства для моделирования и экспериментального исследования физического процесса. В качестве такого процесса как пример решается задача о сваливающейся со стола цепочке.

Метод дискретизации по времени

Время и физические величины в нашем мире непрерывны. Они могут принимать любые значения — вещественные числа.

Чтобы упростить решение сложных задач, будем рассматривать физические явления и значения физических величин в дискретные моменты

Рассматривая время как дискретную величину, необходимо получить формулы, описывающие переход значений параметров физической задачи из состояния в момент времени к их значениям в момент времени Эти формулы, обычно достаточно простые, заменят дифференциальные уравнения. Их простота объясняется тем, что мы будем считать, что изменяющиеся параметры задачи остаются постоянными в пределах интервала . Затем можно будет составить алгоритм, с помощью которого выполняется расчет параметров задачи последовательно для моментов времени . Таким образом, традиционные уравнения можно заменить алгоритмами.

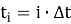
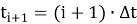
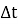
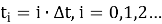
Общая схема такого алгоритма показана на рис. 2. Можно предположить, что решение, полученное для дискретного времени, будет близким к решению в реальном мире, если интервал между значениями времени будет очень маленьким.

Традиционно, численное решение сложных задач получают, записывая сложные математические уравнения (математическую модель) и затем применяя к ним численные методы решения с дискретизацией по времени к математической модели. Отличие предлагаемого подхода заключается в том, что такая дискретизация применяется непосредственно к физическому процессу.

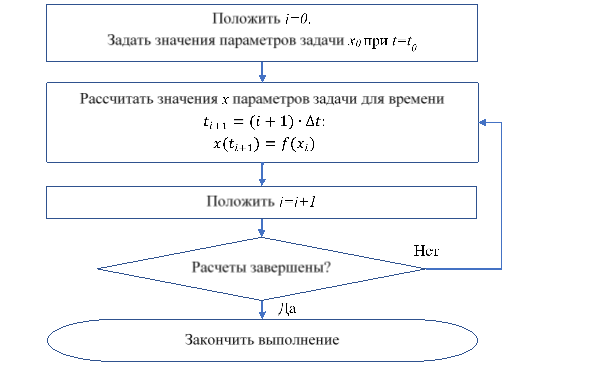
Рис. 1. Общая схема алгоритма расчета

Задача о цепочке

Рассмотрим на примере, как, используя предложенный подход, можно сложную задачу решить школьными методами.

Рассмотрим цепочку длиной L которая свисает с шероховатого стола на длину L ₀ , которой достаточно, чтобы цепочка начала соскальзывать (рис. 2). Длина цепочки меньше высоты стола. Необходимо построить график зависимости положения конца свисающей цепочки от времени, найти время, за которое цепочка полностью соскользнет со стола, а также ее скорость в этот момент. Коэффициент трения цепочки о стол μ.

Рассмотрим силы, действующие на части цепочки (Рис.4). На все звенья свисающей части действует сила тяжести. Пусть в момент со стола свисает часть цепочки массой . На нее действует сила тяжести

.

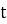
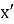
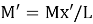
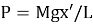
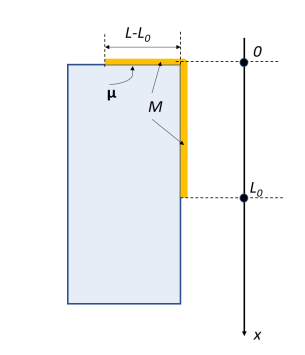
Рис. 2. Задача о цепочке на столе

На столе в этот момент времени лежит часть цепочки длиной и массой .Пусть на столе лежат r звеньев цепи. Масса каждого звена . На каждое звено действует сила тяжести и сила реакции опоры . Сила трения, действующая на каждое звено . Силу трения, действующую на лежащую часть цепочки в момент времени t найдем, суммируя силы трения, действующие на звенья цепочки. Получаем, что на всю часть цепи на столе действует сила трения

.

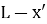
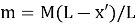
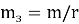
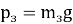
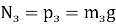
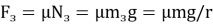
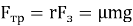
В процессе скольжения цепочка будет двигаться под действием разности сил и

.

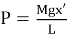
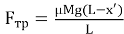
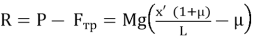
Движение начнется, только если в начальный момент R больше 0 (рис.3).

Проблема точного решения этой задачи состоит в том, что разность сил R — величина переменная и зависит от положения цепочки. Поэтому движение цепочки не будет ни равномерным, ни равноускоренным. Записать уравнение, описывающее такое движение, в рамках школьных знаний нельзя.

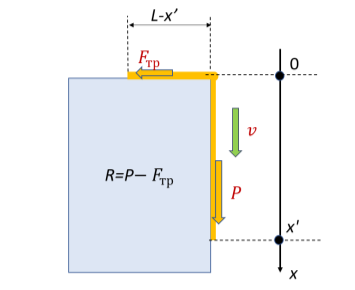
Рис. 3. Скольжение и сваливание цепочки

Будем рассматривать положение конца цепочки в дискретные моменты времени . Считаем, что в пределах малого, но конечного интервал времени силы, действующие на цепочку, неизменяются : и Рассмотрим движение цепочки с момента времени до + пределах этого интервала t _i ≤ t < t _i+1 будем считать неизменным, таким же как в момент времени t _i :

;

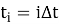
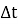
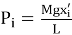
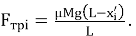
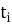
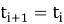
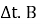
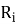
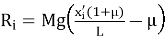
Тогда скорость в конце этого интервала в момент t _i+1 из второго закона Ньютона:

.

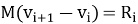
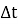
Отсюда

.

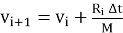
Новую координату свисающего конца цепочки , найдем, прибавив к ее координате в момент времени перемещение ее конца, равное произведению средней скорости цепочки за отрезок времени [ , ] на прошедшее время :

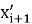
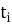
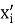
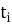
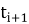
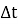
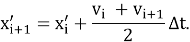
Наконец, зная координату конца цепочки в момент времени пересчитаем новое значение в этот момент времени:

;

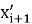
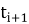
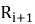
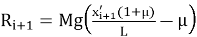
Полученные формулы простые и не требуют знаний высшей математики. Из этих формул получаем алгоритм расчета (рис.4): вместо сложных уравнений мы получили простейший алгоритм, который сможет запрограммировать школьник, имеющий даже малый опыт программирования.

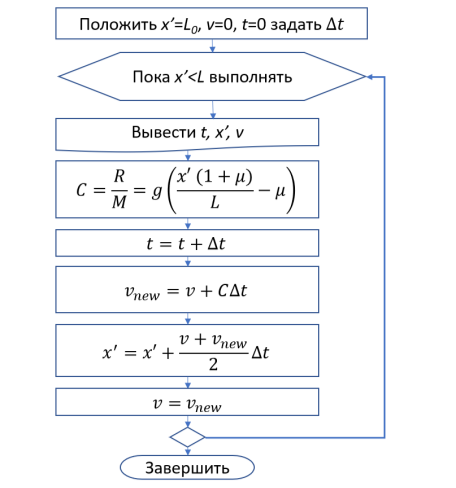
Рис. 4. Блок-схема алгоритма расчета

Коэффициент трения цепочки о стол можно найти экспериментально, наклоняя стол и определив, при каком угле наклона стола начинается соскальзывание цепочки. Формула для вычисления коэффициента трения известна из школьного курса физики . Средний по трем изменениям угол начала скольжения цепочки, использовавшийся в дальнейшем в эксперименте, α=16,8 ⁰ . μ = tg α = 0,3.

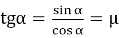
Расчеты по написанной на С++ программе выполнялись на микроконтроллерном устройстве для следующих параметров задачи:

– Длина цепочки L=0,72 м.

– Начальная длина свешивающейся части L ₀ = 0,32 м.

– Коэффициент трения μ = 0,3

– Шаг по времени Δt = 10– ³ c

По результатам расчетов был построен график зависимости координаты (длины) свешивающегося конца от времени (рис. 5). Были получены следующие числовые значения:

– Время сваливания 0,46 с.

– Скорость в момент сваливания 2,23 м/с.

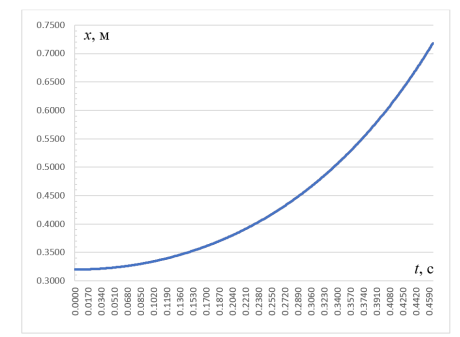
Рис. 5. График зависимости длины свешивающейся части цепочки от времени

Экспериментальное исследование

Экспериментальная установка была построена на базе разработанного автором этого проекта прототипа программно-аппаратного микроконтроллерного комплекса для подготовки будущих инженеров [2] (рис. 6).

Рис. 6. Прототип программно-аппаратного комплекса, использовавшегося для автоматизации эксперимента

Основой стенда является печатная плата, на которой размещен микроконтроллер, множество датчиков, собирающих информацию о температуре, атмосферном давлении, влажности, освещенности, движении людей, разъемы для подключения внешних устройств. Открытые интерфейсы позволяют изменять конфигурацию и расширять возможности стенда,

На основе этого прототипа в Белорусском государственном университете разработаны промышленные образцы этого комплекса. Комплекс был удостоен диплома международной выставке Digital Expo 25

Для проведения эксперимента была построена специальная установка (рис. 7), которая позволяла измерять время, когда конец цепочки проходит определенные расстояния в процессе его падения. Для этого в начальный момент времени цепочка фиксировалась электромагнитом. Пару светодиод-фототранзистор можно было перемещать по вертикальным рейкам, изменяя расстояние, на котором фиксировалось время пересечения светового луча концом цепочки. К свисающему концу цепочки был приклеен маленький кусочек фольги, который пересекал инфракрасный луч от светодиода к фототранзистору, который работал в ключевом режиме. Когда световой луч

Рис. 7. Общий вид экспериментальной установки

падал на транзистор, он был открыт, и цифровой пин микроконтроллера замыкался через него на землю. В момент пересечения луча концом цепочки транзистор закрывался и на пин поступало напряжение 5 В. Время с момента отпускания цепочки до срабатывания фототранзистора фиксировалось микроконтроллером и выводилось на экран. Перемещая пару светодиод-фототранзистор вдоль направления падения, получили зависимость времени от расстояния. На рис. 8 показана часть электрической схемы стенда, которая использовалась для автоматизации эксперимента. К силовому выходу стенда, который управляется Mosfet транзистором, подключается электромагнит. К цифровым пинам 5 и 7 подключаются светодиод и фототранзистор. При нажатии кнопки на электромагнит подается напряжение, и он отпускает цепочку. Начинается измерение времени, которое останавливается, когда свисающий конец цепочки пересекает луч инфракрасного светодиода.

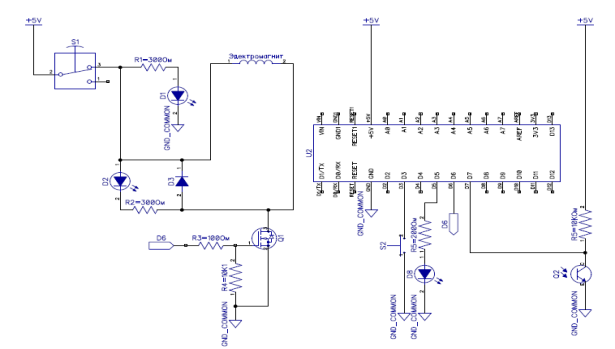
Рис. 8. Электрическая схема используемой части устройства

Установка управляется программой, алгоритм которой показан на рис.9.

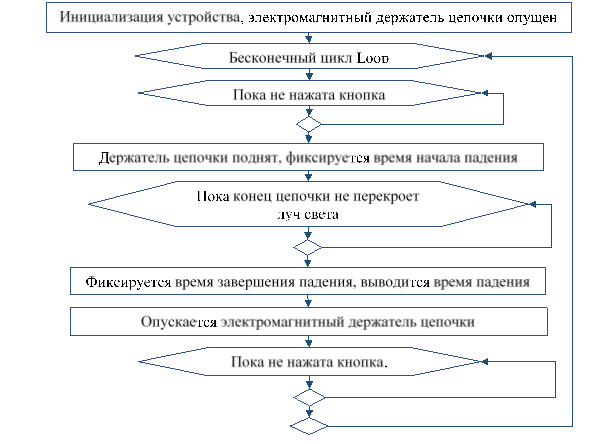
Рис. 9. Блок-схема алгоритма программы автоматизации измерений

Эксперимент проводился для тех же начальных параметров, которые использовались для расчетов. Усреднялись результаты пяти измерений для каждого выбранного расстояния от уровня стола. Расстояние выбиралось местом установки пары светодиод-фототранзистор в отверстиях стенда, расстояние между которыми составляло 2 сантиметра.

В результате эксперимента были получены значения, приведенные в табл. 1.

Имея таблицу с экспериментальными результатами, можем наглядно сравнить их с расчетом, нанеся их на график рис. 10.

Таблица 1

Из таблицы и рисунка видно, что результаты расчетов подтверждаются экспериментально. Максимальная относительная погрешность измерения времени относительно расчетного значения составила менее 8 %. Некоторый разброс значений можно объяснить тем, что на больших расстояниях листочек фольги, прикрепленный к концу цепочки иногда касался боковых направляющих и тормозился о них. В целом, эксперимент подтверждает возможность применения разработанного аппаратно-программного комплекса для измерения малых интервалов времени с использованием датчика на основе фототранзистора.

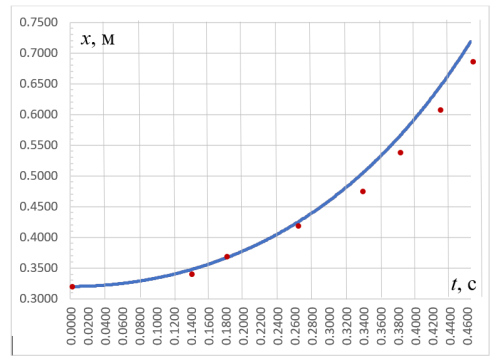
Рис. 10. Сравнение расчетов и эксперимента

Оценка скорости цепочки на последних сантиметрах сваливания была получена как изменение координаты цепочки 0,08 м, которое разделили на интервал времени 0,041 с. Таким образом, экспериментальная оценка скорости сваливания дает результат 1,95 м/с, что неплохо согласуется с расчетной скоростью 2,23 м/с. Оценка скорости получена с ошибкой 12,6 %, что для данного способа оценки можно считать удовлетворительным.

Исследование численного решения

Сравним результаты расчета с точным решением, которое можно получить, решив соответствующее дифференциальное уравнение:

;

;

;

;

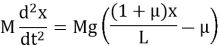
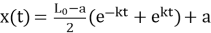
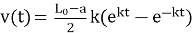
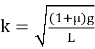
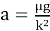
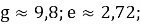
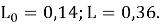
Сравнение результатов расчетов при Δt = 10– ³ c, теории, результатов численного моделирования и эксперимента приведены в табл. 2. Для сравнения взяты моменты времени, зафиксированные в ходе эксперимента. Видим, что результаты расчета для дискретного времени совпали с точным решением, полученным по теоретическим формулам с точностью не хуже трех значащих цифр.

Таблица 2

Было выполнено исследование зависимости погрешности численных расчетов положения конца цепочки от шага дискретизации Δt и достигнутого времени. Для этого были выполнены расчеты для трех значений шага дискретизации, сведенные в таблицу 3. Расчетные значения сравнивались со значениями, вычисленными по теоретическим формулам, приведенным выше. На рис. 11 для наглядности показана зависимость относительной погрешности численных расчетов по предложенному алгоритму от времени.

Таблица 3

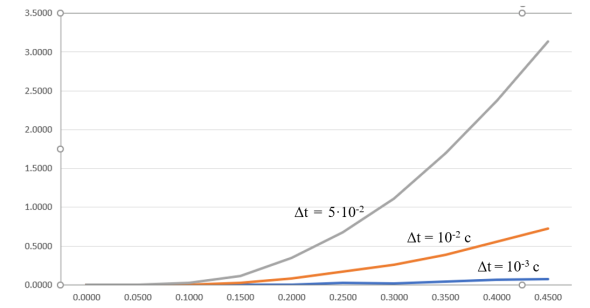
Рис. 11. Зависимость относительной погрешности вычислений от времени

Из табл. 3 и рис. 11 можно сделать следующие выводы:

– с уменьшением шага дискретизации по времени абсолютная и относительная погрешности расчетов уменьшаются;

– с ростом времени и, соответственно с ростом числа шагов по времени, относительная и абсолютная погрешности возрастают.

Рост погрешности с числом шагов по времени объясняется тем, что, по сути, полученные для численных расчетов формулы являются рекуррентными. Это значит, что каждое новое значение координаты цепочки x _i+1 рассчитывается на основе предыдущего x _i . Такая рекурсия характерна тем, что погрешности, возникающие на каждом шаге из-за конечной точности чисел в памяти компьютера и конечного значения шага по времени накапливаются в процессе вычислений.

Заключение

Решение физических задач возможно путем замены непрерывного времени на дискретные значения и уравнений на алгоритмы. Благодаря этому такие решения могут быть намного проще. На примере показано при применении предложенного метода погрешность расчетов снижается при уменьшении шага дискретизации. Вместе с тем, с увеличением числа шагов по времени может нарастать накапливающаяся погрешность, что объясняется рекурсивным характером расчетных формул.

Показано, что ранее разработанный автором работы прототип программно-аппаратного микроконтроллерного комплекса для подготовки будущих инженеров может успешно использоваться при проведении физического эксперимента для измерения малых интервалов времени. Результаты расчетов подтверждены экспериментально.

В процессе выполнения работы были предложены оригинальные алгоритмы численного моделирования физических задач, разработано реализующее их программное обеспечение на языке С++. Разработана экспериментальная установка и программа автоматизации измерений для микроконтроллерного комплекса. Поставлен эксперимент. Выполнено исследование погрешностей предложенного метода моделирования.

Литература:

1. Лукашенко: подготовка образованных и ответственных специалистов — стратегическое направление для экономики. — Беларусь сегодня. 17.10.2025 г. [Электронный ресурс]. Режим доступа: https://www.sb.by/articles/lukashenko-podgotovka-obrazovannykh-i-otvetstvennykh-spetsialistov-strategicheskoe-napravlenie-dlya-.html. Дата доступа: 05.11.2025 г.
2. В БГУ разработали комплекс для подготовки будущих инженеров. — Беларусь сегодня. 28.05.2025 г. [электронный ресурс] https://www.sb.by/articles/v-bgu-razrabotali-kompleks-dlya-podgotovki-budushchikh-inzhenerov.html Дата доступа: 05.11.2025 г.
3. Посадка на Луну. Информация для пользователя. [Электронный ресурс]. Режим доступа: https://ik.imagekit.io/79xdah2uoq/games/moon-lander/Moon_lander_1_1_IbWZv1w7v.pdf?ik-sdk-version=javascript-1.4.3&updatedAt=1650300772430. Дата доступа: 05.11.2025 г.
4. Иродов И. Е. Задачи по общей физике / И. Е. Иродов. М. Бином, 2020.
5. Общий физический практикум: механика /П. Н. Кривцов и др. ФГБОУ ВО «Университет «Дубна», 2022.