Введение.
В истории математики традиционно выделяются несколько этапов развития математических знаний:
- Формирование понятия геометрической фигуры и числа.
- Появление счёта.
- Изобретение арифметических операций.
- Формирование понятия измерения, которое позволило сравнивать длины, площади и объёмы.
- «Один и два»
Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет.
Количество предметов, например, овец, изображалось нанесением чёрточек или засечек на какой — либо твёрдой поверхности: камне, глине, дереве (до изобретения бумаги было ещё очень и очень далеко). Каждой овце в такой записи соответствовала одна чёрточка.
Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. И не случайно у некоторых племен Австралии до самого последнего времени было только два числительных: «один» и «два».
Урапун (1); Окоза (2); Окоза-Урапун (3); Окоза-Окоза (4).
Далее шло «много». И десять — «много», и сто — «много».
2. Древнеегипетская десятичная система исчисления
Для облегчения счёта люди стали группировать предметы по 3, 5, 10 штук. Естественно, что при подсчёте использовались пальцы рук, поэтому первыми появились знаки для обозначения группы предметов из 5 и 10 штук (единиц).
В древнеегипетской системе счисления использовались специальные знаки для обозначения чисел 1, 10, 100. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из них повторялась не более девяти раз.
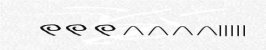
Рис. 1 Запись числа 345 в древнеегипетской системе счисления
3. Древнеримская система.
У римлян были специальные обозначения не только для чисел 1, 10, 100 и 1000, но и для чисел 5, 50 и 500. Римские цифры имели такой вид: 1 — I, 5 — V, 10 — X, 50 — L, 100 — C, 500 — D и 1000 — M. Возможно, знак V означал раскрытую руку, а X — две такие руки.
Так что, если вы увидите на старинном доме сделанную римскими цифрами надпись MDCCCXLIV, то легко определите, что он построен в 1844 году.
4. Двенадцатеричная система счисления.
Широкое распространение имела в древности и двенадцатеричная система, происхождение которой связано со счетом на пальцах: за единицу счета принимались фаланги (отдельные суставы) четырех пальцев одной руки, которые при счете перебирались большим пальцем той же руки. Число 12 называлось «дюжина». Сохранился обычай считать многие предметы не десятками а дюжинами, например, столовые приборы в сервизе или стулья в мебельном гарнитуре.
5.Вавилонская шестидесятеричная система
Числа в этой системе счисления составлялись из знаков двух видов: прямой клин служил для обозначения единиц, а лежачий клин — для обозначения десятков.
![]()
Рис. 2 Число 32 в вавилонской системе
Многое из шестидесятеричной системы вавилонян дошло и до наших дней: деление часа на 60 минут, а минуты на 60 секунд. Следуя разработанной в древнем Вавилоне системе, мы и сейчас дели окружность на 360 частей (градусов).
6.Славянская система счисления
Данная система счисления является алфавитной, т. е. вместо цифр используются буквы алфавита. Данная система счисления применялась нашими предками и была достаточно сложной, т. к. использовала в качестве цифр 27 букв.
|
|
аз |
1 |
|
и |
10 |
|
рцы |
100 |
|
|
веди |
2 |
|
како |
20 |
|
слово |
200 |
|
|
глаголь |
3 |
|
люди |
30 |
|
твёрдо |
300 |
Рис. 3 Славянская система счисления
7.Арабские цифры.
Те очень удобные цифры, которыми мы пользуемся сегодня, изобрели индийцы: они так любили вычислять, что даже математические книги писали в стихах!
Это был набор из 9 цифр от 1 до 9. Каждая цифра записывалась так, чтобы ей соответствовало количество углов. Например, в цифре 1 — один угол, в цифре 2 — два угла, в цифре 3 — три. И так до 9. Нуля еще не существовало, он появился позже. Вместо него просто оставляли пустое место.
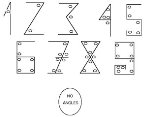
Рис. 4 Арабские цифры
Индийские цифры так сильно упростили вычисления, что со временем завоевали весь мир. В Европу эти цифры попали благодаря арабам, поэтому индийские цифры называют арабскими.
8.Двоичная система счисления.
В этой системе всего две цифры — 0 и 1. Основание системы — число 2. Самая правая цифра числа показывает число единиц, следующая цифра — число двоек, следующая — число четверок и т. д. Двоичная система счисления позволяет закодировать любое натуральное число — представить его в виде последовательности нулей и единиц.
Заключение.
Я начал свой рассказ с двоичной системы счисления туземцев и закончил двоичной системой счисления, используемой в современных компьютерах. Вот так самая молодая система счисления является и самой старой.
Литература:
- Берман Г. Н. Счёт и число (как люди учились считать). 1956.
- Глейзер Г. И. История математики в школе. IV-VI классы. 1981.
- Депман И. Я. История арифметики. 1965.
- www.radostmoya.ru/project/akademiya_zanimatelnyh_nauk_matematika/
- www.wikipedia.org/
- http://irnik.narod.ru/