Данная статья посвящена применению дифференциального уравнения в практике, а именно для описания модели распространения инфекционного заболевания гриппа.
Ключевые слова: дифференциальное уравнение, математическая модель, алгебра и начала математического анализа, грипп.
Ежегодно в России просходит вспышка и распространение гриппа, несмотря на вакцинацию и другие профилактические мероприятия. Возможно ли с помощью математического анализа, методов и моделей предугадать сколько заболевших будет в будущем, зная размер населения России и количество заболевших ранее?
В биологию, геологию и другие «описательные науки» математика пришла по-настоящему только во второй половине XX века. Первые попытки математически описать биологические процессы относятся к моделям популяционной динамики. Эта область математической биологии и в дальнейшем служила математическим полигоном, на котором «отрабатывались» математические модели в разных областях биологии.
Самая первая известная модель, сформулированная в биологической постановке, — знаменитый ряд Фибоначчи, который приводит в своем труде Леонардо из Пизы в XIII веке. Это ряд чисел, описывающий количество пар кроликов, если кролики начинают размножаться со второго месяца и каждый месяц дают потомство в виде пары кроликов. Ряд представляет последовательность чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,... [4].
Математические методы для изучения заболеваний были впервые применены в 1760 году Даниэлем Бернулли, который оценивал с их помощью эффективность различных способов прививки против оспы. В 1840 году Уильям Фарр успешно описал данные по смертности от оспы в Англии и Уэльсе за период с 1837 по 1839 год кривой нормального распределения. Этот метод был развит Джоном Браунли, опубликовавшим в 1906 году статью «Статистический подход к иммунной защите: теория эпидемий» (Brownlee, 1906 г.), в которой он сопоставлял ряды эпидемиологических данных на основе распределения Пирсона [2].
Решение многих задач естествознания, биологии, медицины и других отраслей научных знаний сводится к математическому моделированию процессов в виде формулы, т. е. в виде функциональной зависимости. Для описания многих биологических процессов и явлений используются математические модели в виде дифференциальных уравнений.
Дифференциальное уравнение — уравнение, связывающее независимые переменные, их функции и производные (дифференциалы) этой функции. Процесс решения дифференциального уравнения называется интегрированием . В отличие от алгебраических уравнений, в результате решения которых получается число (несколько чисел), результатом решения дифференциальных уравнений является функция (семейство функций) [5].
Грипп — острое респираторное вирусное заболевание, вызываемое вирусами гриппа и поражающее в первую очередь верхние дыхательные пути, также поражает бронхи, в более редких случаях — лёгкие. Выделяется среди острых респираторных вирусных инфекций (ОРВИ) у людей из-за возможного тяжёлого течения болезни. Грипп ассоциируется с высокой смертностью во время пандемий, эпидемий и спорадических вспышек.
Сегодня для исследования инфекционных заболеваний существует модель SIR. Эта аббревиатура происходит от английских слов Susceptible — Infected — Recovered , буквально означающих «восприимчивые — инфицированные — выздоровевшие». Под «восприимчивыми» имеется в виду еще не инфицированные организмы.
В рамках этой модели с помощью систем дифференциальных уравнений описывается динамика распространения заболевания.
Система уравнений SIR:
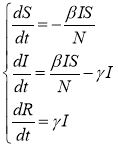
где
S(t) — численность восприимчивых индивидов в момент времени t ;
I(t) — численность инфицированных индивидов в момент времени t ;
R(t) — численность переболевших индивидов в момент времени t ;
N — общая численность населения;
На основе SIR-модели были разработаны следующие её типы:
SIRS: «Восприимчивые — инфицированные — выздоровевшие — восприимчивые». Модель для описания динамики заболеваний с временным иммунитетом.
SEIR: «Восприимчивые — контактировавшие с инфекцией (Exposed) — инфицированные — выздоровевшие». Модель для описания распространения заболеваний с инкубационным периодом.
SIS: «Восприимчивые — инфицированные — восприимчивые». Модель для рспространения заболевания, к которому не вырабатывается иммунитет.
MSEIR: «Наделенные иммунитетом от рождения (Maternally derived immunity) — восприимчивые — контактировавшие с инфекцией (Exposed) — инфицированные — выздоровевшие». Модель, учитывающая иммунитет детей, приобретенный внутриутробно.
Для рассчета прогноза количества заболевщих гриппом была выбрана модель SIS, являющаяся наиболее подходящей, так как данная упрощённая модель предназначена для заболеваний, к которым не вырабатывается иммунитет — в их числе грипп.
Система уравнений SIS:
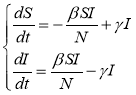
Коэффициенты β и γ можно менять при условии, что β > 0 и 0 < γ < 1.
Параметр β > 0 характеризует интенсивность контактов индивидов с последующим инфицированием (среднее число контактов между инфицированным и неинфицированными индивидами в день, при которых происходит передача заболевания). Значение параметра β было принято за единицу, это означает, что при контакте здорового индивида с инфицированным заражение первого неизбежно. [10]
Параметр 0 < γ < 1 характеризует интенсивность перехода инфицированных индивидов вновь в группу восприимчивых. Значение этого параметра было найдено через среднее время заразности T
r
:
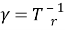
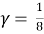
С сайта Роспотребнадзора были взяты данные по заболеваемости гриппом в России за 2018–2019 годы [11].
С сайта Росстата были взяты данные по численности населения России за 2018–2019 годы [12].
С помощью подстановки значений параметров
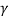
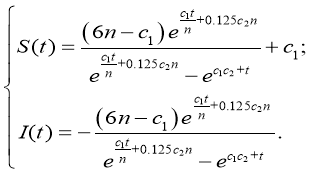
В данную систему уравнений подставили значения за 2018 год:
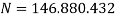
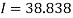
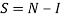
Все вычисления были выполнены с помощью математического пакета Maple 17, было найдено частное решение системы (рис 1).

Рис. 1
Частное решение системы можно представить в виде:

В данную систему подставляется значение
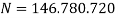

Рис. 2
В результате вычислений было найдено приближённое значениe I(t)=39075,46158, которое отличалось от реального значения I(t)=37310 на 1765,46158, т. е. погрешность составила примерно 1800 человек. Таким образом, с помощью системы дифференциальных уравненияй можно спрогнозировать количество заболевших человек и принять меры для предотвращения большой смертности.
Литература:
- Братусь А. С., Новожилов А. С., Платонов А. П. Динамические системы и модели биологии. М.: Физматлит, 2010. 400 с.
- Леоненко В. Н. Математическая эпидемиология. Учебно–методическое пособие по выполнению лабораторных работ. — СПб: Университет ИТМО, 2018. — 38 с.
- Максимова, Н. Н. Математическое моделирование. Учебно-методическое пособие. — Благовещенск: Изд-во АмГУ, 2019. — 88 с.
- Ризниченко Г. Ю. Лекции по математическим моделям в биологии. Часть 1. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2002, 232 стр.
- Смирнова, В. Б., Морозова Л. Е. Обыкновенные дифференциальные уравнения: учеб. пособие /СПбГАСУ. — СПб., 2010. –87 c.
- Математическое моделирование (курс лекций, сост. П. С. Сабуров) [электронный ресурс] — http://op.vlsu.ru/fileadmin/Programmy/Bacalavr_academ/20.03.01/Metod_doc/15–16/Metod_Lek_MatMod_20.03.01_04052016.pdf
- Математический справочник [электронный ресурс] — https://zaochnik.com/spravochnik/matematika/differentsialnye-uravnenija/vidy-differentsialnyh-uravnenij/
- Справочник [электронный ресурс] — https://spravochnick.ru/informacionnye_tehnologii/informacionnye_modeli_i_modelirovanie/model_hischnik-zhertva/
- Статья [электронный ресурс] — https://truengineer.github.io/2020–04–25-sir-model/
- Роспотребнадзор [электронный ресурс] — https://www.rospotrebnadzor.ru/activities/statistical-materials/
- Росстат [электронный ресурсс] — https://rosstat.gov.ru/compendium/document/13282

