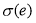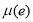В статье автор представляет программное обеспечение системы прогнозирования временных рядов для использования в системах технической диагностики.
Ключевые слова: программное обеспечение, техническая диагностика, прогнозирование, временной ряд.
В современном мире временные ряды стали одним из главных предметов анализа протекающих процессов в различных областях научно-технической, экономической, социальной и других сферах деятельности человека. Анализ временных рядов позволяет извлекать полезную информацию, выявлять закономерности, осуществлять прогнозы. Техническая диагностика является одной из тех областей, где использование методов анализа и прогнозирования временных рядов диагностических параметров имеет первостепенное значение для эффективной эксплуатации технических систем.
При разработке системы прогнозирования временных рядов диагностических параметров технических систем (ТС) необходимо учитывать, что, с точки зрения теории технической диагностики, любая техническая система является динамической системой, функционирующей в пространстве известных информационных признаков [1]. Таким образом, в процессе функционирования ТС, характеристики диагностических параметров могут меняться, следовательно система прогнозирования должна обеспечивать возможность адаптации модели временного ряда и метода прогнозирования к изменяющимся условиям.
Среди специализированного программного обеспечения (ПО), решающего задачи прогнозирования временных рядов, можно выделить два типа ПО — desktop-приложения и специализированные программные инструменты для построения систем прогнозирования временных рядов. В ряду desktop-приложений можно рассмотреть ПО CaterpillarSSA и Novo Forecast [2, 3]. Среди программных инструментов — библиотека Prophet, платформа NeuralProphet и платформа FEDOT [4, 5, 6].
Обзор аналогов программного обеспечения (ПО) и инструментальных средств (ИС) для прогнозирования временных рядов показал следующее:
— возможности ПО и ИС для прогнозирования временных рядов ограничены моделями, на основе которых вычисляется прогноз и наоборот — модели прогнозирования временных последовательностей, используемые при прогнозировании, определяют класс задач, которые могут решать ПО и ИС;
— сложность ПО и ИС определяется набором используемых моделей временных рядов и алгоритмом их применения;
— использование в ПО и ИС искусственных нейронных сетей (ИНС) и алгоритмов машинного обучения позволяет упростить для пользователя решение задачи прогнозирования временны последовательностей.
Для прогнозирования временных рядов диагностических параметров необходимо ПО, с помощью которого можно было бы не только выполнить прогнозирование, но и провести предварительную обработку входных данных, а также проанализировать входные данные на наличие различных составляющих и их связь с другими диагностическими параметрами. Также ПО должно обеспечивать возможность использования различных моделей временных рядов и методов их прогнозирования.
В конечном итоге нами была разработано ПО для прогнозирования временных рядов. В основе работы ПО лежит метод разложения входной последовательности на периодические компоненты синусоидальной формы с последующим прогнозированием каждой из компонент предиктором на основе нейронной сети. Для получения окончательного решения результаты прогнозирования компонент суммируются [7, 8].
Данный метод позволяет гибко подходить к построению моделей временных рядов и выбору предикторов для прогнозирования компонент. Для примера, на рис. 1 представлен результат прогнозирования диагностического параметра сопротивления изоляции якорной цепи привода поворота шагающего экскаватора ЭШ 40.100. Наблюдения производились каждые 12 часов — в начале рабочей смены, в соответствии с режимом работы оперативного персонала. Сопротивление изоляции измерялось мегаомметром ЭСО210/2 (измерительное напряжение 1000 В) с пределом шкалы измерения 50 МОм, поэтому значения сопротивления изоляции находятся в диапазоне 0–50 МОм.
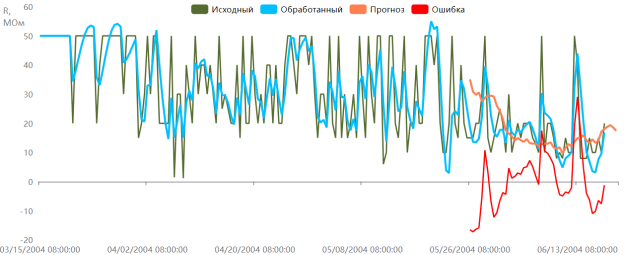
Рис. 1. Пример работы ПО системы прогнозирования
На рис. 1 представлены исходный сигнал, обработанный сигнал, а также результат прогнозирования и график ошибки прогнозирования временного ряда для интервала упреждения D=4 , что с учетом интервала дискретизации выборки Δt = 12 ч , составляет 48 часов или двое суток наблюдений.
В таблице 1 представлены настройки алгоритмов обработки и прогнозирования для данной временной последовательности.
Таблица 1
Параметры алгоритмов обработки и прогнозирования
|
№ |
Наименование параметра |
Значение |
|
1 |
Алгоритм обработки | |
|
1.1 |
Количество компонент декомпозиции |
66 компонент |
|
1.2 |
Количество компонент, используемых в модели временного ряда |
13 компонент |
|
1.3 |
Интервал упреждения для модели временного ряда |
4 отсчета |
|
2 |
Алгоритм прогнозирования | |
|
2.1 |
Обучающая выборка |
168 отсчетов на интервале [0; 167] |
|
2.2 |
Тестовая выборка |
22 отсчета на интервале [168; 189] |
|
2.3 |
Тип предиктора |
ИНС прямого распространения (FNN) с линейной функцией активации |
|
2.4 |
Метод настройки (обучения) предиктора |
Алгоритм Левенберга-Марквардта |
|
2.5 |
Размерность вектора входных данных |
3 |
|
2.6 |
Размерность вектора выходных данных |
1 |
Согласно данным, представленным в таблице 1 для прогнозирования всех компонент использовалась одинаковая модель предиктора. При использование линейной активационной функции нет смысла строить многослойные сети, так как линейную сеть с любым количеством слоев и нейронов в ней можно свести, путем линейных преобразований, к модели простого адаптивного сумматора. Для настройки ИНС использовался алгоритм Левенберга-Марквардта, который, при сравнимой с другими алгоритмами оптимизации точности, обеспечивает высокую скорость сходимости.
Результаты прогнозирования сопротивления изоляции якорной цепи привода поворота экскаватора ЭШ 40.100 представлены в таблице 2.
Таблица 2
Результаты прогнозирования сопротивления изоляции
|
Параметр |
Среднеквадратическое отклонение ошибки,
|
Среднее значение ошибки,
|
|
Значение |
10,56 |
2,54 |
Использованный в программном обеспечении системы прогнозирования временных рядов диагностических параметров технических систем подход к обработке и прогнозированию временных рядов позволяет гибко подходить к построению моделей временных рядов, а также обеспечивает выбор модели предиктора и алгоритмов оптимизации для прогнозирования данных временных рядов с различными характеристиками.
Литература:
- Проников А. С. Надежность машин. –М.: Машиностроение, 1978. — 592 с., ил. — (Межиздательская серия «надежность и качество»).
- Программная реализация метода «Гусеница» CaterpillarSSA 3.40 // [электронный ресурс]. URL: https://www.gistatgroup.com/gus/programs.html (дата обращения 03.09.2024).
- Novo Forecast// [электронный ресурс]. URL: https://novoforecast.com/ (дата обращения 03.09.2024).
- Prophet// [электронный ресурс]. URL: https://github.com/facebook/prophet (дата обращения 03.09.2024).
- NeuralProphet// [электронный ресурс]. URL: https://neuralprophet.com/ (дата обращения 03.09.2024).
- FEDOT// [электронный ресурс]. URL: https://github.com/aimclub/FEDOT (дата обращения 03.09.2024).
- Шамаль М. А., Карякин А. Л. Прогнозирование диагностических параметров электротехнических комплексов главных приводов мощных экскаваторов// Журнал «Научное обозрение. Технические науки». — 2014. — № 2. — С. 219–220.