Числа всегда были в жизни человека и с развитием цивилизации люди все больше нуждались в числах. Числа — это неотъемлемая часть нашего современного мира. Они применяются во всех сферах человеческой деятельности. Все что мы делаем, зависит от чисел.
Числа применяются во всех сферах человеческой деятельности. Все что мы делаем, зависит от чисел. Нам приходиться считать, измерять, вычислять и решать самые разные проблемы — и все это лучше делать с числами. Числа окружают нас и всячески помогают нам в наших делах. Они — инструменты для счета. Без чисел мы не знали бы, какой сегодня день и который час. Мы не смогли бы ничего купить, не сосчитали бы своих вещей, не поговорили бы о том, чего нам не хватает. Без чисел современный мир остановится.
Что такое число π? Это простое отношение длины окружности к её диаметру. Эта величина постоянна для всех окружностей. Одна из загадок π состоит в том, что его невозможно вычислить точно. Оно не выражается простым отношением типа 22:7. Значит, π — иррациональное число. Число π важно для ученых и инженеров. Все круглое и все, что движется по кругу (колеса, планеты и др.), содержит π. Без π люди не смогли бы создать автомобили, понять движение планет или сосчитать, сколько бобов поместится в банку.
Ещё одно необычное число φ(фи) или 1,6180339… Математики и художники знали о нем многие тысячи лет, а люди приписывали ему волшебные свойства. Число φ обладает странными свойствами. Если умножить его на само себя, то получится ровно столько же, как если прибавить 1. При делении любого числа ряда Фибоначчи на предшествующее всегда получается число, близкое к φ, но никогда точно ему не равное. Древние греки считали число φ магическим, так как оно всегда присутствовало в символах, почитавшихся священными. Например, в пятиконечной звезде отношение длинного отрезка к короткому точно равно числу φ.
Какое самое большое число можно себе представить? Какой бы ни был ответ, к нему всегда можно прибавить 1, потом еще 1, и еще, и еще… Фактически нет предела тому, насколько большими (или насколько малыми) могут быть числа. Математики называют это бесконечность. Бесконечности бывают разные, и одни больше других. Последовательность целых чисел (1,2,3…) называется счетной бесконечностью. Но между целыми числами размещаются иррациональные числа, такие, как π и φ. Эти иррациональные числа составляют несчетную бесконечность, которая, по мнению экспертов, бесконечно больше обычной бесконечности. Иными словами, бесконечность больше бесконечности.
Загадкой математики является тайна простых чисел — это их распределение между остальными числами: произвольное, без какого-либо порядка. Математики годами пытались найти этот порядок, но безуспешно. А отсутствие порядка означает, что простые числа следует отыскивать одно за другим. Малые простые числа легко найти с помощью так называемого «решета Эратосфена», но как насчет больших? Математики нашли несколько очень больших простых чисел. 23 августа 2008 г. компьютеры отдела математики университета в Лос-Анджелесе (Калифорния) обнаружили гигантское 12 978 189-значное простое число 2 43 112 609– 1, а 6 сентября 2008 г, компьютер инженера Ханса Микаэла Элвинича из города Лагенфельда (Германия) открыл 11185272 -значное простое число: 2 37 156 667 -1. Участники международного интернет-проекта, подключившие свои компьютеры к исследованию и поиску рекордных по величине простых чисел, получили крупное денежное вознаграждение от фонда Electronic Frontier Foundation (см. сайт www. mersenne.org).
Интересны не только числа, но и задачи, связанные с ними. Так называемые математические фокусы — это отдельный раздел задач, включающий в себя задачи геометрического содержания, логические задачи, задачи на применение свойств чисел, задачи комбинаторики и теории вероятности. Для решения таких заданий нет единого алгоритма. Каждый вид требует своего метода решения. К ним относятся анализ и синтез, доказательство от противного или с использованием свойств, проведение аналогий и другие.
Примеры «математических фокусов»:
«Угадай зачеркнутую цифру».
Если задумать какое-нибудь многозначное число, например, число 847. Затем найти сумму цифр этого числа (8+4+7=19) и отнять ее от задуманного числа. Получится: 847–19=828. В том числе, которое получится, зачеркнуть цифру — безразлично какую, и сообщить все остальные. Тогда можно назвать зачеркнутую цифру, хотя не знаете задуманного числа.
Ключом этого фокуса является свойство чисел. Потому что если от какого-либо числа отнять сумму его цифр, то останется число, делящееся на 9 без остатка, иначе говоря, такое, сумма цифр которого делится на 9. В самом деле, пусть в задуманном числе а — цифра сотен, в — цифра десятков, с — цифра единиц. Значит, всего в этом числе единиц 100а+10в+с. Отнимая от этого числа сумму цифр (а+в+с), получим: 100а+10в+с — (а+в+с)=99а+9в=9(11а+в), т. е. число, делящееся на 9. При выполнении фокуса может случиться, что сумма сообщенных вам цифр сама делится на 9, например, 4 и 5. Это показывает, что зачеркнутая цифра либо 0, либо 9. Тогда ответ: 0 или 9.
«Отгадывание разности»
Написать трехзначное число с неодинаковыми крайними цифрами и составить новое число из тех же цифр, но записанных в обратном порядке. Вычислите разность между этими числами, вычитая из большего меньшее, и назвать только последнюю цифру результата. По этим данным можно назвать весь полученный результат.
Почему это можно сделать?
Пусть загадали число АВС, тогда число, записанное цифрами в обратном порядке, будет: СВА.
Если А>С, то АВС > СВА.
Составим разность:
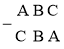
Последней цифрой разности будет 10СА, так как С<А, то для вычитания занимаем 10 единиц из числа десятков В. Средней цифрой разности будет 10(В1)В=9 (число десятков уменьшилось на 1 и для вычитания занимаем 10 десятков из числа сотен А). Таким образом, средняя цифра разности всегда будет 9. Первой цифрой разности будет: (А1)С. Сумма первой и последней цифр разности будет: А1С10СА=9. Из этого следует, что чтобы найти всю разность, нужно лишь найти первую цифру, а ей является разность 9 и названной цифры.
«Одно свойство простых дробей»
Написать произвольное количество разных простых дробей, числители и знаменатели которых положительны. Составить новую дробь, числитель которой равнялся бы сумме всех числителей, а знаменатель — сумме всех знаменателей написанных вами дробей. Эта дробь обязательно будет больше самой меньшей, но меньше самой большей из написанных вами дробей. Пусть
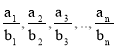
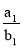
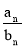
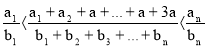
Значит,
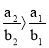
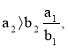
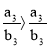
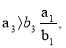
Отсюда следует, что
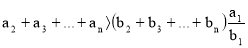
Прибавим к левой части этого неравенства
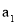
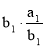
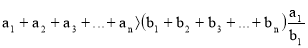
Отсюда
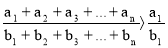
Аналогично доказывается и вторая часть, то есть что:
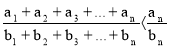
Литература:
- Болл Джонни. «Подумай о числе». Dorling Kindersley Limited, 2005.
- «Занимательная наука». «ЗАО Издательский Дом Ридерз Дайджест», 2008.
- Интернет-ресурс, www.mersenne.org
- Кордемский Б. А. «Математическая смекалка» — 10-е изд., переработ. и доп. –М.:Юнисам, МДС, 2004.
- Перельман Я.И; Под редакцией и с доп. Болтянского В.Г; «Наука», М.:2005.

