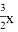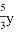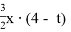Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного желания решить трудную задачу невозможно, но при наличии такого — возможно. Где есть желание, найдется путь.
Д. Пойа
Зачем вообще мыслить нестандартно? Люди, мечтающие состояться как личность, должны научиться мыслить нестандартно, уйти от шаблонов, рутины и скуки. Человек, мыслящий иначе, чем все, — это творец, искатель, вырвавшийся из плена шаблонов и стереотипов. Смогли бы сделать открытия, реализовать себя, оставить свой след на Земле Никола Тесла, Альберт Эйнштейн, Томас Эдисон и другие великие люди, если бы они мыслили стандартно? Конечно же, нет.
При решении подобных задач развивается мышление, сообразительность, повышается уровень математической грамотности. В большинстве своём они встречаются на вступительных испытаниях в ВУЗы и на олимпиадах. Это проверка того, насколько широко вы способны мыслить и способны ли вообще. Да и некоторые текстовые задачи не удается решить стандартными методами. Тем не менее, рассмотрим возможные подходы, которые могут быть применены к таким задачам в различных ситуациях.
Ситуация 1 . Даже при удачном выборе переменных их число превышает число уравнений. В этом случае можно попытаться сгруппировать неизвестные и переобозначить получившиеся группы, уменьшив при этом число новых переменных. Часто в таких задачах метод группировки подсказывает сам вопрос задачи. Обычно требуется найти не сами переменные, а какую-то их комбинацию.
Другим выходом из сложившейся ситуации может быть поиск дополнительных условий. Иногда такими условиями являются особенности геометрического расположения объектов задачи, которые можно записать, используя уравнения и неравенства из геометрии (теоремы синусов, косинусов; неравенство треугольника и т. п.).
Ситуация 2 . Текстовые условия задачи не переводятся однозначно в систему алгебраических условий. Это означает, что возможно встретилась задача с альтернативным условием, то есть такая задача, в которой требуется рассмотреть несколько равноправных возможных условий. Обычно подробный анализ этих условий позволяет отбросить все альтернативы, кроме одной.
Ситуация 3 . Аналитическая запись текстового условия задачи приводит к смешанной системе, содержащей уравнения и неравенства. Часто это означает, что система может быть решена методом минимаксов.
Конечно, изложенные ситуации не могут охватить все многообразие нестандартных текстовых задач.
Рассмотрим на примерах как можно использовать указанные ситуации.
Пример 1 . (ВМК МГУ, 1989)
Из пункта А в пункт В вышел пешеход. Вслед за ним через 2 часа из пункта А выехал велосипедист, а еще через 30 минут –мотоциклист. Пешеход, велосипедист и мотоциклист двигались равномерно и без остановок. Через некоторое время после выезда мотоциклиста оказалось, что к этому времени все трое преодолели одинаковую часть пути от А до В. На сколько минут раньше пешехода в пункт В прибыл велосипедист, если пешеход прибыл в пункт В на 1 час позже мотоциклиста?
Решение.
Изобразим путь из А в В в виде отрезка АВ.

Обозначим точкой С на отрезке АВ то место, где мотоциклист и велосипедист одновременно догнали пешехода. Расстояние АС обозначим через p, а СВ — через q.
|
S(км) |
v(км/час) |
t (час) | |
|
пешеход |
P |
X |
p/x |
|
велосипедист |
P |
Y |
p/y |
|
мотоциклист |
P |
Z |
p/z |
|
пешеход |
Q |
X |
q/x |
|
велосипедист |
Q |
Y |
q/y |
|
мотоциклист |
Q |
Z |
q/z |
Из условия задачи следует, что
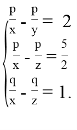
В условии задачи требуется найти величину: q/x — q/y.
Выразим эту величину из системы (1). Введем обозначения: а = 1/ x — 1/ y;
b =1/ x — 1/ z. Тогда уравнения системы (1) примут вид:
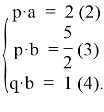
Нужно найти величину q·а. Перемножая равенства (2) и (4), получаем, что
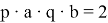
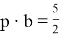
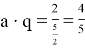
Ответ: 4/5 часа или 48 минут.
Пример 2 . (ВМК МГУ, 1973)
Из пункта А одновременно выходят три пешехода и одновременно возвращаются в тот же пункт, обойдя маршрут, состоящий из прямолинейных отрезков AB, ВC, CD, DA, которые образуют равнобокую трапецию (AB и CD — боковые стороны). На указанных отрезках скорости всех пешеходов постоянны и равны: у первого 6, 8, 5, и 8 км/час соответственно, а у второго — 7, 7, 6 и 8 км/час соответственно. Скорость третьего пешехода на каждом из отрезков равна либо 7 км/час, либо 8 км/час, причем на всем пути он меняет скорость один раз. Определите отношение меньшего основания трапеции к боковой стороне.
Решение .
Изобразим маршруты движения пешеходов на рисунке.
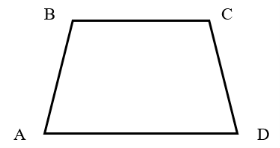
Отметим условность приведенного рисунка: на нем длина DA> ВC, хотя в действительности может быть наоборот. Поэтому предстоит выяснить, какое расстояние наименьшее, и найти отношение наименьшего расстояния к длине боковой стороны. Введем обозначения:
|
AB |
x |
|
ВC |
y |
|
CD |
x |
|
DA |
z |
По условию
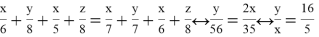
Рассмотрим все возможные варианты скоростей движения третьего пешехода на отрезках маршрута AВCD:
|
AB |
В C |
CD |
DA |
|
7 км/час |
7 км/час |
7 км/час |
8 км/час |
|
7 км/час |
7 км/час |
8 км/час |
8 км/час |
|
7 км/час |
8 км/час |
8 км/час |
8 км/час |
|
8 км/час |
8 км/час |
8 км/час |
7 км/час |
|
8 км/час |
8 км/час |
7 км/час |
7 км/час |
|
8 км/час |
7 км/час |
7 км/час |
7 км/час |
Сравним первый, второй, третий и шестой варианты с движением второго пешехода, а четвертый и пятый варианты — с движением первого пешехода.
-
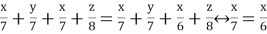
-
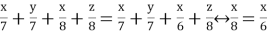
-
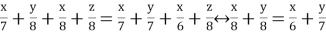
-
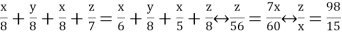
-
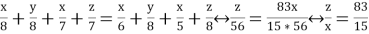
-
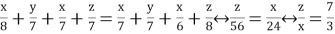
Для отбора получившихся решений должны выполняться следующие неравенства
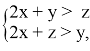
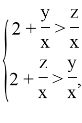
|
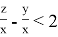
Используя (2), получим, что только (5) удовлетворяет неравенству (6). Рассмотрим систему
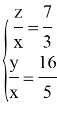
Получаем, что
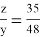
Ответ: 7/3.
Решение задачи показывает, что не всегда сделанный к задаче чертеж реально отражает все ее соотношения.
Пример 3 .
С завода на стройку нужно перевезти 24 больших и 510 маленьких бетонных блоков. Доставка блоков осуществляется автомашинами, каждая из которых вмещает в себя 44 маленьких блока и имеет грузоподъемность 10 тонн. Вес маленького блока составляет 0,2 тонны, большой блок весит 3,6 тонн и занимает место 14 маленьких. Найти минимальное число рейсов, достаточное для перевозки всех блоков.
Решение.
Предположим, что все блоки перевезли за q рейсов. Тогда должны выполняться следующие соотношения:
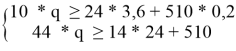
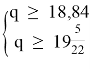
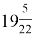
Наименьшее целое число, которое удовлетворяет неравенству, равно 20.
Докажем теперь, что 20 рейсов будет достаточно для перевозки всех блоков. Для этого рассмотрим конкретную схему перевозки. За каждый из первых 12 рейсов можно перевезти два больших блока и 14 маленьких блоков. При этом выполняются все ограничения по массе и размерам. Нагружая по 44 маленьких блока каждый рейс (это возможно) мы могли бы за 8 рейсов перевезти 352 маленьких блока.
Ответ: 20 рейсов.
Пример 4.
В магазине имеется три вида наборов игрушек: мягкие, металлические, пластмассовые. Детский сад купил по одному набору пластмассовых и металлических игрушек и 4 набора мягких игрушек, при этом количество игрушек совпало с количеством детей в детском саду. Если бы купили 4 набора металлических и один набор мягких игрушек, то 57 детям игрушек бы не досталось. Количество игрушек, составляющих 4 набора пластмассовых и 1 мягких на 41 меньше числа детей. Сколько детей было в детском саду, если, купив по три набора игрушек каждого вида, детский сад не обеспечил бы всех детей игрушками?
Решение.
|
Вид набора |
Количество игрушек в наборе |
|
Металлические |
X |
|
Пластмассовые |
Y |
|
Мягкие |
Z |
k-количество детей в детском саду.
Из условия задачи получаем следующую систему:
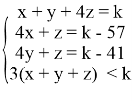
Вычтем из первого и третьего поочередно второе уравнение, получим:
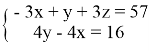
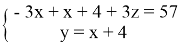
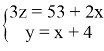
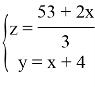
Подставим в уравнение
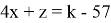
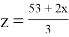
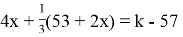
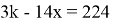
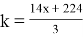
-
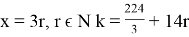
-
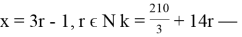
-
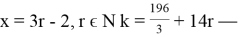
Условию
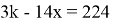
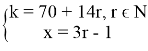
и только они. Заменяя теперь у на х+4 и 3z на 2х+53 в неравенстве
3(x+y+z)
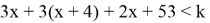
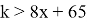
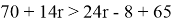
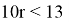
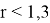
Условию

Ответ: 84.
Пример 5 .
Путь из села в город идет сначала по грунтовой дороге, а затем по шоссе. Из села в город в 7 часов утра выехал автомобилист, и одновременно с ним из города в село выехал мотоциклист. Мотоциклист двигался по шоссе быстрее, чем по грунтовой дороге в 1


Решение.
Предположим, что автомобилист сможет приехать в город до 11 часов 15 минут, если он весь путь из села в город будет ехать с первоначальной скоростью. Если на движение по грунтовой дороге он затрачивает t часов, то на движение по шоссе он затрачивает (4- t) часов. При неизменной скорости весь путь у него займет
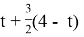
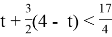
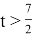
|
Скорость на грунтовой дороге |
Скорость на шоссе | |
|
автомобилист |
х км/ч |
|
|
мотоциклист |
у км/ч |
|
После встречи мотоциклист двигался 3 часа и прошел тот же путь, что и автомобилист за 9/4 часа (то есть до встречи). Поэтому
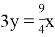
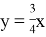
|
Длина грунтового участка дороги |
х∙ t км |
|
Длина шоссейного участка дороги |
|
Мотоциклист движется по шоссе
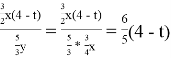
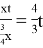


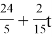
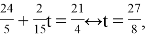
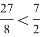
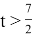
Ответ: не может.
Пример 6 .
Автотранспортное предприятие располагает парком автобусов для перевозки пассажиров. По подсчетам экономистов, эксплуатационные расходы составляют 11,4 тыс. руб. на 1 км при пробеге 100 тыс. км. в год и 13,4 тыс. руб. на 1 км при пробеге 75 тыс. км в год. Требуется:
а) представить переменные и постоянные затраты в виде формулы:
у= a + bх;
б) рассчитать, какова будет сумма эксплуатационных расходов, если автобус пройдет 85 тыс. км в год.
Решение.
Из приведенных данных видно, что минимальные эксплуатационные затраты составляют 11400 рублей, а максимальные — 13400 рублей. Минимальный пробег — 75000 км в год, максимальный пробег — 100000 км в год.
Разница в уровнях затрат составляет 2000 рублей (13400–11400). Разница в пробеге — 25000 км. Тогда ставка переменных расходов на 1 км пробега составит 0,08 руб. (2000 / 25000).
Вычислим общую величину переменных расходов для максимального и минимального уровней:
75000 * 0,08 = 6000 рублей;100000 * 0,08 = 8000 рублей
Тогда величина постоянных затрат составит:
11400–6000 = 5400 рублей; 13400–8000 = 5400 рублей
Уравнение затрат для данного примера будет иметь вид:
у = 5400 + 0,08 х, где у — общая величина эксплуатационных
расходов; х — величина пробега. Сумма эксплуатационных расходов составит 12200 рублей, если автобус пройдет 85000 км в год:
у= 5400 + 0,08 * 85000 = 5400 + 6800 =12200 рублей.
Таким образом, подставляя в данное уравнение различные значения по пробегу, можно установить общую величину эксплуатационных расходов.
Пример 7 .
Тринадцать пиратов делят клад золотых монет на палубе шхуны. При попытке разделить клад поровну оказалось, что остается 8 монет. Налетевшим штормом двух пиратов смыло за борт. Когда оставшиеся пираты снова стали поровну делить клад, то лишними оказались 3 золотые монеты. Затем в перестрелке погибли еще три пирата. Когда уцелевшие пираты опять стали делить клад, то на этот раз оказалось, что остается 5 монет. Из какого количества монет состоял клад, если для его переноски достаточно сундука, вмещающего 500 золотых монет?
Решение.
Пусть К — количество монет, из которых состоит клад. К≤500. x, y, z — число монет, которые достались бы каждому пирату при первом, втором, третьем делении соответственно. Согласно условию задачи, имеем следующую систему:
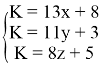
Рассмотрим сначала уравнение
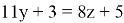
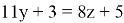
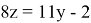
Перебирая все возможные остатки отделения y на 8, находим, что решением последнего уравнения являются
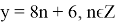
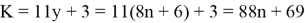
Ответ: 333 монеты.
Пример 8.
Мастер делает за один час целое число деталей, большее 5, а ученик — на 2 детали меньше. Мастер выполняет заказ за целое число часов, а два ученика вместе — на 1 час быстрее. Из какого числа деталей состоит заказ?
Решение.
Пусть мастер за 1 час делает k деталей (k>5), тогда ученик (k-2) детали. Пусть мастер выполнит заказ за t часов, тогда, согласно условию задачи, имеем уравнение:
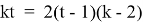
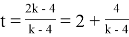
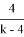
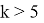
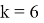
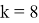
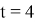
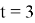
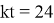
Ответ: 24 детали.
Пример 9 (СПбГУ, 2016)
Цены минуты телефонного разговора и одного sms положительны и кратны копейке. Суммарная стоимость 13 минут разговора и 120 sms равна 23 рубля 60 копеек. Найти цену одного sms.
Решение.
Пусть m копеек — стоимость 1 минуты разговора, а n копеек — стоимость 1 sms, причём
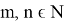
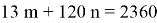
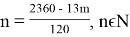
Разложим числа на множители:
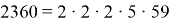
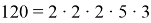
Теперь представим m в виде
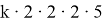
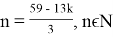
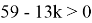
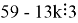
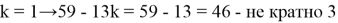
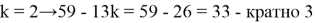
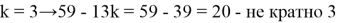
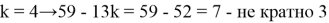
Таким образом,
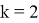
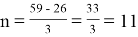
Ответ: 11 копеек.
Пример 10.
Из пунктов А и В навстречу друг другу вышли одновременно два поезда. Каждый из них двигался сначала равноускорено (начальные скорости поездов равны нулю, ускорения различны), а затем, достигнув некоторой скорости, — равномерно. Отношение скоростей равномерного движения поездов равно


Решение:
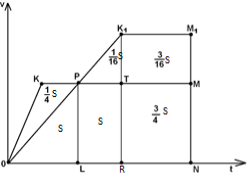
Рассмотрим графики, изображающие зависимость скорости от времени, для каждого поезда. Для одного поезда графиком является ломаная ОКМ, для другого ОК
1
М
1
. Длина пройденного пути равна площади соответствующей фигуры под графиком. По условию поезда прошли одно и то же расстояние за одно время, поэтому мы можем сказать, что площади трапеций ОКМN и ОК
1
М
1
N равны; значит, площади фигур ОКР и РК
1
М
1
М также равны. Площадь ОКРL равна

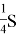

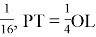
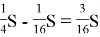
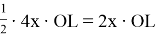
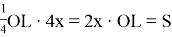
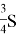
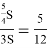
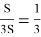
Ответ:
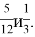
Упражнения.
- (ВМК МГУ,1973) Из пункта А одновременно стартуют три бегуна и одновременно финишируют в том же пункте, пробежав по маршруту, состоящему из прямолинейных отрезков АВ, ВС, СА, образующих треугольник АВС. На каждом из указанных отрезков скорости у бегунов постоянны и равны: у первого — 10 км / ч, 16 км / ч и 14 км / ч соответственно; у второго — 12 км / ч, 10 км / ч и 16 км / ч соответственно. Третий бегун в пунктах В и С оказывается не один и меняет скорость на маршруте один раз. Установить, является ли треугольник АВС остроугольным или тупоугольным. (Ответ: тупоугольным)
- Вася и Петя поделили между собой 39 орехов. Число орехов, доставшихся любому из них, меньше удвоенного числа орехов, доставшихся другому. Квадрат трети числа орехов, доставшихся Пете, меньше числа орехов, доставшихся Васе. Сколько орехов у каждого? (Ответ:25 и 14 орехов)
-
Пункт А находится на берегу реки, ширина которой 400 м, скорость течения 3 км / ч. Пункт В расположен ниже по течению в 4 км от А (если В
1
— проекция В на берег, на котором расположен А, то АВ
1
=4 км), на расстоянии 2 км 680 м от противоположного берега (А и В — по разные стороны реки). Турист выехал из А на лодке, пересек реку, оставил на берегу лодку, дошел до В и вернулся тем же путем. На всех участках, по реке и по суше, он двигался прямолинейно. Скорость лодки в стоячей воде 5 км / ч, скорость передвижения туриста пешком 3,2 км / ч. За какое наименьшее время мог проделать свое путешествие турист? (Ответ: Наименьшее время, за которое турист мог проделать свое путешествие 3
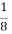
- (Экономический факультет МГУ, 1992) Фабрика получила заказ на изготовление 1005 деталей первого типа и 2010 деталей второго типа. Каждый из 192 рабочих фабрики затрачивает на изготовление двух деталей первого типа время, за которое он мог бы изготовить одну деталь второго типа. Каким образом следует разделить рабочих фабрики на две бригады, чтобы выполнить заказ за наименьшее время, при условии, что обе бригады приступят к работе одновременно, и каждая из бригад будет занята изготовление деталей только одного типа? (Ответ: 39; 153)
-
(Физический факультет МГУ, 1970) Имеется два картофельных поля. Сначала первое поле было убрано бригадой
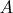
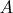
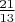
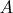
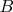
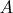
- (ВМК МГУ, 1987) Из пункта А в пункт Б по железной дороге нужно перевезти по 20 больших и 250 малых контейнеров. Один вагон вмещает 30 малых контейнеров, вес каждого составляет 2 тонны. Большой контейнер занимает место 9 малых контейнеров и весит 30 тонн. Грузоподъёмность вагона 80 тонн. Найти минимальное число вагонов, достаточное для перевозки всех контейнеров. (Ответ: 15 вагонов)
Литература:
- Методы решения задач по алгебре: от простых до самых сложных / С. В. Кравцев и др. — М.Издательство: «Экзамен», 2003–544с.
- Как решать задачи по математике / И. И. Мельников, И. Н. Сергеев. Москва, издательство МГУ, 1990г.
- Задачи по математике. Алгебра. /В. В. Вавилов, И. И. Мельников и др. Москва, издательство «Наука», 1987г.
- Математика. Профильный уровень. Задания с развернутым ответом / Ю. В. Садовничий. Издательство «Экзамен», Москва, 2019г.