В данной статье рассматриваются понятия четырехмерного пространства и гиперкуба, а также вопросы практического применения тессеракта к решению транспортных задач. Проводится анализ методов решения транспортных задач с помощью гиперкуба, математических формул и САПР MathCAD.
Ключевые слова: гиперкуб, тессеракт, транспортная задача, САПР MathCAD.
Цель работы: изучение методов решения транспортных задач и выбор наиболее рационального.
Задачи работы:
- Проанализировать специальную литературу по теме исследования.
- Изучить измерения пространства-времени и обосновать возможно решения транспортной задачи с помощью многомерного пространства.
- Изучить способы решения транспортных задач.
- Выявить преимущества и недостатки методов решения транспортных задач.
Введение
Перевозка и доставка грузов, планирование с учётом необходимых товаров в разном регионе, городе является неотъемлемой частью экономики как теоретической, так и практической. Давайте ненадолго представим, что мы предприниматели и открываем новую сеть магазинов. Прибыль у хозяина будет складываться только тогда, когда доходы от продажи будут превышать расходы. Но как минимизировать последние? Как, куда и откуда нужно транспортировать товары с наименьшими затратами на перевозку, когда у тебя десятки вариантов путей? Как наиболее рационально расположить магазины по городу, чтобы они были одновременно близки и к потребителю, и к поставщику?
На эти вопросы отвечает логистика, которая предлагает разные варианты решения задач оптимизации. Есть много способов решения этих задач. В данном исследовании рассмотрена транспортная задача и способы её решения, один из которых предусматривает использование многомерного пространства.
Многомерное пространство.
Пространство — форма существования материальных объектов и процессов. Оно состоит из трёх плюс одного измерения. Первое — это длина. Второе измерение — это ширина. Длинная и ширина вместе образуют двухмерное пространство или плоскость. Третье измерение — это высота. Длинна, ширина и высота образуют объём или пространство. Четвёртое измерение — не является пространственным, как первые три. Оно одно в своём роде. Мы не можем его увидеть или потрогать, однако мы очень хорошо его чувствуем. Четвёртое измерение — это ВРЕМЯ.
На самом деле, количество измерений не ограничено, в математике их может быть сколько угодно, но существуют они для решения разных задач и не имеют общих названий. Для их обозначения в геометрии, существует такое понятие как гиперкуб. Гиперкуб — обобщение куба с произвольным числом измерений
Для решения транспортной задачи рассматривается 4 вида гиперкубов: отрезок, квадрат, куб и тессеракт. Как это может быть видно: все они отлично демонстрируют пространственные и временное измерения, а также их непосредственную взаимосвязь, поскольку существование последующего гиперкуба невозможно без предыдущего.
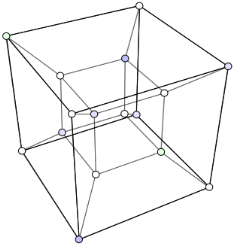
Рис. 1. Тессеракт
Транспортная задача
Однако, какое это имеет отношение к решению транспортной задачи? Прежде чем ответить на этот вопрос, узнаем, а что такое транспортная задача. Транспортная задача — математическая задача линейного программирования об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления с минимальными затратами.
Условие этой задачи таково. Однородный груз сосредоточен у m поставщиков в объемах a1, a2,... am. Данный груз необходимо доставить n потребителям в объемах b1, b2... bn. Известны Cij, i=1,2,...m; j=1,2,...n — стоимости перевозки единиц груза от каждого i-го поставщика каждому j-му потребителю. Переменными транспортной задачи являются xij — объемы перевозок от i-го поставщика каждому j-му потребителю.
Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью, и суммарные затраты на перевозку всех грузов являются минимальными.
Таблица 1
Исходные данные транспортной задачи

Математическая формулировка транспортной задачи: найти переменные задачи X=(xij), i=1,2,...,m; j=1,2,...,n, удовлетворяющие системе ограничений, при которой запасы всех m поставщиков вывозятся полностью, удовлетворены запросы всех n потребителей, условиям не отрицательности и обеспечивающие минимум целевой функции.
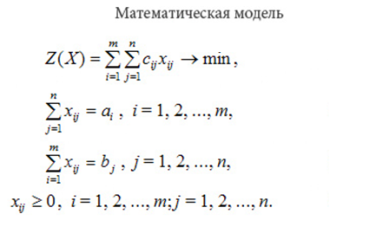
В рассмотренной в рамках данной статьи модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей. Решаются такие задачи несколькими способами. В статье рассмотрены математический метод, метод с использованием гиперкуба и с помощью системы автоматизированного проектирования (САПР) MathCAD.
Решение транспортной задачи методом потенциалов.
В качестве предмета исследования будет выступать следующая задача. В таблице приведены исходные данные транспортной задачи: расстояние от поставщика к потребителю в километрах, и спрос потребителя в тоннах некоего товара. Сформулируйте экономико-математическую модель транспортной задачи, распределительным методом найдите оптимальный план перевозок.
Таблица 2
Пример транспортной задачи (исходные данные)
|
Поставщики |
Возможности поставщиков |
Потребители иих спрос | ||||
|
I |
II |
III |
IV |
V | ||
|
150 |
350 |
200 |
100 |
100 | ||
|
I |
500 |
3 |
3 |
5 |
3 |
1 |
|
II |
300 |
4 |
3 |
2 |
4 |
5 |
|
III |
100 |
3 |
7 |
5 |
4 |
2 |
Целевая функция L=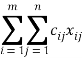 в рассматриваемой задаче стремится к минимуму. Проверим условие того, что данная модель задачи закрытая: 150+350+200+100+100=900 и 500+300+100=900. Построим начальный опорный план, методом минимальной стоимости, согласно которому, сперва заполним ячейки с минимальными затратами на перевозку. И когда весь груз распределён, перейдем к оптимизированию полученного плана.
в рассматриваемой задаче стремится к минимуму. Проверим условие того, что данная модель задачи закрытая: 150+350+200+100+100=900 и 500+300+100=900. Построим начальный опорный план, методом минимальной стоимости, согласно которому, сперва заполним ячейки с минимальными затратами на перевозку. И когда весь груз распределён, перейдем к оптимизированию полученного плана.
Проверка плана транспортной задачи в описываемом методе на оптимальность осуществляется с помощью потенциалов. Потенциалы — это такие числа, которые по определенным правилам назначаются каждой строке и каждому столбцу. Потенциалы строк обозначим ui, потенциалы столбцов — vj. Они могут принимать любые значения. Однако удобнее работать с положительными, целыми и относительно небольшими числами. Такой потенциал первоначально назначается любой строке или столбцу. В нашем случае зададим потенциал второй строке равный нулю (U2=0). Подсчёт потенциалов осуществим по условию: Ui+Vj=Сij
Сперва с помощью этой формулы и потенциала 2 строки рассчитаем потенциалы столбцов, а затем потенциалы оставшихся строк. Получим следующую таблицу.
Таблица 3
План перевозок
|
|
150 |
350 |
200 |
100 |
100 |
Ui |
|
500 |
3 |
3 (+) 100 |
5(-) 200 |
3 100 |
1 100 |
0 |
|
300 |
4 50 |
3(-) 250 |
(+) 2 |
4 |
5 |
0 |
|
100 |
3 100 |
7 |
5 |
4 |
2 |
-1 |
|
Vj |
4 |
3 |
5 |
3 |
1 |
Общая стоимость перевозок согласно этому плану равняется 2850 ед. Проверяя условие оптимальности в свободных клетках по условию Ui+Vj≤сij, получим что в клетках с координатами (1,1) и (2,3) условие не выполняется, следовательно, требуется улучшение плана. Способ улучшения плана — переброска груза по циклу. Для этого каждой клетке цикла присваивают знаки (+) или (-), чередуя их, начиная с (+) в клетке, в которой не выполняется условие оптимальности. Затем выбирают наименьшую перевозку из базисных клеток со знаком (-) и прибавляют её в клетку со знаком (+) и вычитают в клетках со знаком (-).
В результате получим следующий таблицу стоимости перевозок.
Таблица 4
Оптимизированный план перевозок
|
|
150 |
350 |
200 |
100 |
100 |
Ui |
|
500 |
3 50 |
3 250 |
5 |
3 100 |
1 100 |
0 |
|
300 |
4 |
3 100 |
2 200 |
4 |
5 |
0 |
|
100 |
3 100 |
7 |
5 |
4 |
2 |
0 |
|
Vj |
3 |
3 |
2 |
3 |
1 |
Подсчитаем стоимость — она равно 2300 ед. и опять проверим план на оптимальность для базисных и для свободных клеток. Поскольку все условия оптимальности соблюдены, то данный план можно считать оптимальным.
Решение транспортной задачи спомощью гиперкуба.
Теперь рассмотрим решение этой же транспортной задачи методом гиперкуба. Для этого метода начальный опорный план составляется с использованием переменных, значения которых в последствии будут найдены при помощи построения сечения гиперкуба в системе координат.
Таблица 5
Опорный план транспортной задачи («метод гиперкуба»)
|
Поставщики |
Возможности поставщиков |
Потребители иих спрос | ||||
|
I |
II |
III |
IV |
V | ||
|
150 |
350 |
200 |
100 |
100 | ||
|
I |
500 |
3x |
3 y |
5 0 |
3 z |
1 500-x-y-z |
|
II |
300 |
4 0 |
3 350-y |
2 200 |
4 100-z |
5 0 |
|
III |
100 |
3 150-x |
7 0 |
5 0 |
4 0 |
2 x-50 |
Как видно из таблицы, некоторые значения были сразу взяты за ноль. Это объясняется невыгодностью перевозок от этого поставщика к этому потребителю.
Учитывая, что все значения, входящие в эту таблицу, должны быть не отрицательны, составим систему неравенств.
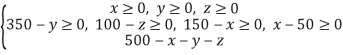
Из двух последних уравнений второй строки следует, что xЄ![]() . Эта система определяет некоторый многогранник, а для того, чтобы его построить изобразим сначала многогранник, определяемый первой и второй строкой данной системы. Это параллелепипед ABCDA1B1C1D1. Уравнение 500-x-y-z определяет плоскость (RGH), пересекающую параллелепипед в точках A1, B, N. На многограннике A1D1C1NADCB выполняются все условия данной системы. Назовём его многогранником ограничений.
. Эта система определяет некоторый многогранник, а для того, чтобы его построить изобразим сначала многогранник, определяемый первой и второй строкой данной системы. Это параллелепипед ABCDA1B1C1D1. Уравнение 500-x-y-z определяет плоскость (RGH), пересекающую параллелепипед в точках A1, B, N. На многограннике A1D1C1NADCB выполняются все условия данной системы. Назовём его многогранником ограничений.
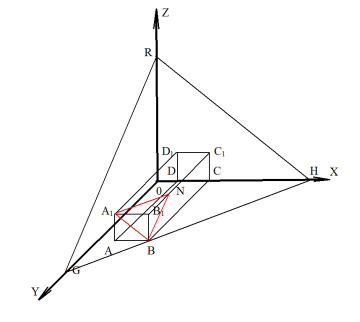
Рис. 2. Многогранник ограничений
Теперь найдём общую стоимость перевозок, сложив и перемножив стоимости и объёмы перевозимого товара. Получаем выражение: x-y-2z+2700
Таким образом задача сводится к отысканию наименьшего значения функции F=2700-(y-x+2z) на многограннике ограничений. Для этого достаточно найти наибольшее значение функции f=y-x+2z, тогда Fmin=2700-Fmax. Вычислив значения Fmax в вершинах многогранника, получаем, что равно оно 500 и достигается в точке А1 с координатами (50;350;100). Подставив значения переменных в таблицу получаем план перевозок:

Видно, что полученный ответ не совпадает с ответом, полученным в решении с использованием метода потенциалов. Потребитель II получает свои 350 тонн груза, однако этот груз ему доставляет поставщик I, согласно полученному плану, тем самым полностью исчерпывает свой лимит в 500 тонн груза. Потребитель же V не получает необходимые ему 100 тонн груза, зато у поставщика II остаются лишние 100 тонн груза. Таким образом, полученный план перевозок не был до конца оптимизирован.
В случае, если, оставшиеся 100 тонн груза у второго поставщика, доставить потребителю v, то получиться новый план перевозок, со стоимостью равной 2300 д. е.
Решение транспортной задачи спомощью САПР MathCAD.


Видно, что план перевозок совпадает с планом, полученным при решении методом потенциалов.
Заключение.
Так или иначе, можно сделать вывод о том, какой из этих трёх способов наиболее рационален: метод потенциалов достаточно объёмен, и предусматривает большое обилие вычислений. Плюс ко всему этот метод — есть цикл, во время которого мы проверяем условия для базисных и свободных клеток. Цикл этот может повторяться сколько угодно, и так и не соблюсти все условия, поэтому данный метод решения транспортной задачи рациональным назвать трудно.
Удобство САПР MathCAD проявляется в возможности использовать одну задачу как шаблон для других, просто меняя числа, однако, чтобы сделать этот шаблон, нужно иметь навык работы с программой, ну и разумеется саму программу, которая стоит совсем не дёшево.
Метод гиперкуба не требует обширных знаний в области математики или IT технологий. Он понятен, быстр в использовании, а также не имеет большого объёма вычислений, что делает его практически идеальным способом решения транспортных задач.
Литература:
- Алексеев Е. Р., Чеснокова О. В. Основы работы в математическом пакете MathCAD. Учебное пособие. — Донецк: ДонНТУ, 2012.
- Болотов В. П. Начертательная геометрия многомерного пространства. — Владивосток: изд-во Морского государственного университета им. Г. И. Невельского, 2003.
- Ибаньес Р. Мир математики. Четвёртое измерение: является ли наш мир частью другой вселенной? — М.: DeAgostini, 2014.
- Рудык Б. М. Ермаков В. И. Общий курс высшей математики для экономистов. — М.: Инфра-М, 2010.
- Хинтон С. Г. Четвертое измерение.- СПб.: Книгоиздательство «Новый человек», 1915.
- Черняк А. А., Новиков В. А. Математика для экономистов на базе MathCAD. — СПб.: БХВ-Петербург, 2003.
- Информационный портал Wikipedia [Электронный ресурс].
- URL:https://ru.wikipedia.org/wiki/Тессеракт (Дата обращения: 07.11.2015г.)

