Однажды Винни Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Задумались и мы…, а сможем ли мы решить эту задачу?
После изучения литературы, посвященной логическим задачам, выяснилось, что пчелки предложили нашему любимому герою известную головоломку на переливание. Практически ни один популярный сборник, связанный с математическими задачами и головоломками, не обходится без раздела «Переливания». Это один из видов старинных занимательных задач, они возникли много веков назад, но до сих пор вызывают интерес у любителей математики и их часто можно встретить в олимпиадных заданиях, что делает их актуальными и сегодня.
Суть этих задач-головоломок сводится к следующему: имея несколько сосудов разного объема, один из которых наполнен жидкостью, требуется разделить ее в каком-либо отношении или отлить какую-либо ее часть при помощи других сосудов за наименьшее число переливаний. Понятно, что для поиска ответа можно перебрать все возможные варианты решения, но это очень долго и неудобно. Поэтому мы решили найти рациональный алгоритм решения задач на переливание.
На первом этапе работы мы, изучили математическую литературу по данной теме. Выяснилось, что можно выделить два основных типа задач на переливание:
– «Открытая система» — задачи, в которых необходимо получить некоторое количество жидкости с помощью нескольких пустых сосудов из бесконечного источника, из которого можно наливать жидкость, и в который ее можно выливать.
– «Закрытая система» — задачи, в которых необходимо разделить жидкость в большей емкости с помощью нескольких меньших по объему емкостей, жидкость можно только переливать из одной емкости в другую.
В задачах на переливания требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи. Если не сказано ничего другого, считается, что все сосуды без делений и нельзя переливать жидкости «на глаз».
Существует несколько методов решения задачи: метод компьютерного моделирования, метод таблиц, метод бильярда.
Рассмотрим эти методы на примере решения задачи Винни-Пуха, которая относится к типу «открытая система».
Метод компьютерного моделирования— основан на применении для решения задач виртуальных лабораторий, позволяющих моделировать реальные ситуации переливания жидкостей. Одна из таких виртуальных лабораторий — программа «ВОДОМАТИКА» (http://www.umapalata.com/design_ru/games/UP_Pereliv.asp?file=UP_Pereliv.swf).
Также для решения задач можно использовать виртуальную лабораторию «Переливания», созданную Лабораторией знаний «Бином».
Метод таблиц— основной прием, который используется при решении задач на переливание. В первом столбце указываются объемы данных сосудов, а в каждом следующем — результат очередного переливания:
|
Ходы |
1 |
2 |
3 |
4 |
5 |
6 |
|
5 л |
5 |
2 |
2 |
- |
5 |
4 |
|
3 л |
- |
3 |
- |
2 |
2 |
3 |
Таблицы позволяют наглядно представить условие задачи или ее ответ, но существенным недостатком этого способа решения является отсутствие четкого алгоритма действий, невозможность предвидеть ближайшие шаги. Составлять такие таблицы можно довольно долго, так и не придя к нужному результату.
Метод бильярда заключается в представлении последовательности переливаний аналогично движению бильярдного шарика по столу особой конструкции с размерами, соответствующими объемам первоначально пустых сосудов.
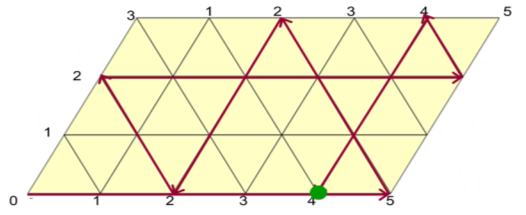
В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали — в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников. Бильярдный шар может перемещаться только вдоль прямых, образующих сетку на параллелограмме. После удара о стороны параллелограмма шар отражается и продолжает движение вдоль выходящего из точки борта, где произошло соударение. При этом каждая точка параллелограмма, в которой происходит соударение, полностью характеризует, сколько воды находится в каждом из сосудов.
Пусть шар находится в левом нижнем углу и после удара начнет перемещаться вверх вдоль левой боковой стороны параллелограмма до тех пор, пока не достигнет верхней стороны. Это означает, что мы полностью наполнили водой малый сосуд. Отразившись, шар покатится вправо вниз и ударится о нижний борт. Это означает, что в большом сосуде 3 литра воды, а в малом сосуде воды нет, то есть мы перелили воду из малого сосуда в большой сосуд. Прослеживая дальнейший путь шара, мы попадаем в точку, которая соответствует состоянию, когда малый сосуд пуст, а в большом сосуде 4 литра воды. Таким образом, получен ответ и указана последовательность переливаний, позволяющих отмерить 4 литра воды.
Прорешав разные задачи типа «открытая система» на переливание различными методами, мы пришли к выводу, что задачи на переливания трудные, но их можно решать по определенному алгоритму:
- Наполнить большую емкость жидкостью из бесконечного источника.
- Перелить из большей емкости в меньшую емкость.
- Вылить жидкость из меньшей емкости.
- Повторить действия 1–3 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
В век новых информационных технологий мы много времени тратим на бессмысленные игры на компьютере. А не лучше ли заняться решением логических задач, пусть даже и с помощью компьютера? Ведь задачи на логику развивают в человеке догадливость, сообразительность и интеллект.
Литература:
1. Ф. Ф. Нагибин, Е. С. Канин Математическая шкатулка М.: Просвещение, 1988
2. И. Ф. Шарыгин Математический винегрет М., АГЕНТСТВО «ОРИОН», 1991
3. Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи на смекалку. — М.: Дрофа, 2003.
4. Сайт «Решение логических задач». Точка доступа: https://sites.google.com/site/resenielog/
5. Сайт «Дидактические игры». Точка доступа: http://www.umapalata.com/design_ru/games/UP_Pereliv.asp?file=UP_Pereliv.swf

