Рассматривается один из вариантов построения математической модели планирования производственного процесса в терминах стохастического программирования и получение детерминированного эквивалента в виде выпуклого программирования.
Ключевые слова: производственный процесс, планирование, неполноты информации, стохастическое программирование, детерминированный эквивалент, математическая модель.
В условиях развивающихся рыночных отношений в Узбекистане резко усложнились задачи управления производственными объектами в целом и предприятиями мелькомбината в частности. Постоянно изменяющиеся технико-технологические и конструктивные характеристики мукомольного производства, а также возрастающая конкуренция на рынке мучных продукций свидетельствуют о том, что наступило время, когда резервы традиционных приемов совершенствования управления производством на предприятиях мукомольного оказались исчерпанными.
Один из перспективных путей решения этих вопросов заключается в повышении эффективности управления производственными объектами на основе использования научно обоснованных методов выработки и принятия решений с применением соответствующего математического аппарата и средств вычислительной техники.
Для решения задач принятия решений применяются различные методы и алгоритмы. Например, Вальд, Гурвиц и Сэвидж предлагают использовать теорию статистических решений и теорию игр. Маршак, Чернов и Рубин, а также Блекуэлл Дю, Гиршик – субъективную вероятность. Методы экспертных систем и искусственного интеллекта: Литвак Б.Г., Бешелев C.JL, Гурвич Ф.Г., Евланов Л.Г., Кутузов В.А., Пятковский О.И. Методы нечеткой логики: Усков А.А., Васильев В.И. Имитационное моделирование: Бусленко Н.П., Багриновский К.А., Форрестер Дж. Методы стохастического программирования: Юдин Д.Б., Песиков Э.Б., Юсупбеков Н.Р., Бекмурадов Т.Ф., Гулямов Ш.М., Игамбердиев Х.З., и другие.
Большинство методов, применяемых для поддержки принятия решений, малопригодны в условиях реального процесса планирования производства на предприятиях переработки зерна в связи со спецификой производства. Поэтому актуальной является задача адаптации существующих методов и формирование новых алгоритмов для поддержки принятия решений с учетом специфики планирования производства мучных продуктов. Внедрение в практику оперативного управления производством мучных продуктов системы поддержки принятия решений с использованием экономико-математических моделей и алгоритмов на сегодняшний день приобретает особое значение и определяется на верхних эшелонах управления предприятиями как одно из приоритетных направлений автоматизации оперативного управления основным производством.
При реалистической постановке задачи планирования производства недопустимо ориентироваться на средние значения располагаемых ресурсов, полученные, например, путем статистической обработки данных о фактических объемах ресурсов в предшествующие периоды времени. Подобное планирование связано с недопустимо высоким риском невыполнения плана. Планирование затрат и выпуска должно ориентироваться на сниженные уровни располагаемых ресурсов. При стремлении к гарантированному результату можно строить планирование, ориентируясь на минимальный уровень располагаемых ресурсов и предельно высокие значения затрат ресурсов. Однако такой подход является полностью лишенным риска и не эффективным, т.к. наихудшая реализация технологических процессов и крайне неудовлетворительное обеспечение ресурсами является мало вероятными событиями. Более рациональным является подход, основанный на введении в ограничения гарантированных с заданными вероятностями нижних уровней располагаемых ресурсов.
В данной работе предлагается использовать методы СП для оптимизации производственной программы мукомольного предприятия в условиях неполной информации об уровнях наличных ресурсов [1,2].
Постановка задачи. Оптимизационная модель, сформулированная в терминах одноэтапной модели СП с вероятностным ограничением, содержит: управляющие переменные – объемы выпуска конечных продуктов по модификациям: систему ограничений, описывающую условия функционирования мукомольного предприятия – обеспеченность лимитирующими производственными ингредиентами, удовлетворение спроса на продукцию. Выполнение директивных значений основных технико-экономических показателей, целевые функции – максимизация (минимизация) некоторого технико-экономического показателя (прибыль, товарная продукция, себестоимость и т. п).
Под допустимым планом понимается такой план (детерминированный – вектор управляющих переменных), для которого вероятность выполнения всех ограничений по лимитирующим ресурсам была бы не меньше заданной величины ![]() . По существу
. По существу ![]() – это вероятность выполнения плана, так как факт выполнения плана зависит от обеспеченности ресурсами.
– это вероятность выполнения плана, так как факт выполнения плана зависит от обеспеченности ресурсами.
Задача объемного планирования заключается в определении в целом за плановый период (год) таких значений управляющих переменных, которые удовлетворяли бы с заданной вероятностью ![]() система ограничений и при этом доставляли экстремум функционалу, реализующему цель управления.
система ограничений и при этом доставляли экстремум функционалу, реализующему цель управления.
Сформулируем задачу расчета оптимального плана с ограничением по ресурсам в вероятностной форме:
найти ![]() (1)
(1)
при условиях: 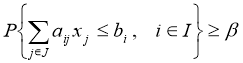 (2)
(2)
0<β≤1, (3)
где x={xj} (jJ) – детерминированный вектор объемов выпуска xj продукта j;
cj – технико-экономический показатель единицы продукта j;
aij – норма расхода ресурса i на единицу продукта j;
I – множество индексов i ресурсов;
J -множество индексов j конечных продуктов;
bi -уровень наличных ресурсов i в плановом периоде (случайная величина);
β – заданный уровень вероятности выполнения системы ограничений.
Ограничения вида ![]() , где
, где ![]() – соответственно нижняя и верхняя границы объема выпуска xj продукта j, предлагаются включенными в условие (2). Из условия (2) следует, что оператор вероятности р применяется ко всей системе линейных неравенств с детерминированной матрицей условий
– соответственно нижняя и верхняя границы объема выпуска xj продукта j, предлагаются включенными в условие (2). Из условия (2) следует, что оператор вероятности р применяется ко всей системе линейных неравенств с детерминированной матрицей условий ![]() и случайным вектором b={bi}.
и случайным вектором b={bi}.
При построении модели делается допущение о статической независимости между компонентами bi вектора b. В качестве возможных функций распределения непрерывных случайных величин bi могут быть приняты: нормальная, экспотенцианальная, Вей- булла, гамма-функция.
Статистическая проверка гипотез о распределении случайных величин bi может быть проведена с помощью известных критериев согласия [3].
В случае справедливости нескольких гипотез о виде распределения некоторого компонента bi вопрос выбора наиболее адекватной статистической модели величины bi решается экспертно.
Одноэтапная модель СП вида (1) – (3) может быть сведена по методике Чарнса-Купера с уровнем риска (1-β) к детерминированному эквиваленту, относящемуся к классу моделей нелинейного программирования с дополнительными переменными βi – вероятностями выполнения ограничений по каждому виду ресурса i.
Детерминированный эквивалент имеет вид:
Найти 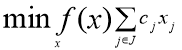 (4).
(4).
при условиях
![]() (5 )
(5 )
![]() (6)
(6)
0<β≤1, (7)
где ![]() - математическое ожидание случайной величины bi ;
- математическое ожидание случайной величины bi ;
ϭi – среднеквадратическое отклонение случайной величины bi;
![]() – квантиль порядка βi;
– квантиль порядка βi;
Π – символ произведения;
Ф(bi) – функция распределения случайной величины bi.
При аппроксимации эмпирических распределений величин bi известными теоретическими распределениями (нормальным, экспоненциальным, вейбулла, гамма – функцией) на основании результатов работы [3] можно сделать вывод о выпуклости допустимых планов задачи (4) – (7). Полученная задача выпуклого программирования может быть решена известными методами, например, методом штрафных функция [1,4]. Из-за сложностей вычислительного характера предлагается упростить модель (4) – (7) путем “расщепления” вероятности β на множество вероятностей βi и подстановки полученных значений βi в ограничение (5). Величины βi определяются экспертно с учетом следующих условий: ![]() . По определению величины
. По определению величины ![]() такая, что
такая, что ![]() . При назначении вероятностей βi следует принять во внимание степень важности ресурсов i для конкретной производственной ситуации. В этом плане представляет интерес двойственные оценки
. При назначении вероятностей βi следует принять во внимание степень важности ресурсов i для конкретной производственной ситуации. В этом плане представляет интерес двойственные оценки ![]() , позволяющие количественно оценить степень «дефицитности» ресурсов i. Известно, что величины
, позволяющие количественно оценить степень «дефицитности» ресурсов i. Известно, что величины ![]() являются частными производными целевой функции f(x) по параметру bi, вычисленными при оптимальном решении x* задачи ЛП, т.е.
являются частными производными целевой функции f(x) по параметру bi, вычисленными при оптимальном решении x* задачи ЛП, т.е.
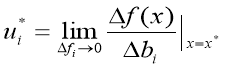 .
.
Величины ![]() , ϭi по своей сути являются «страховкой на случайность». То есть при планировании учитывается гарантированный уровень ресурса i.
, ϭi по своей сути являются «страховкой на случайность». То есть при планировании учитывается гарантированный уровень ресурса i.
Величина ![]() является нижней границей доверительного интервала для величины bi, соответствующего заданной вероятности βi.
является нижней границей доверительного интервала для величины bi, соответствующего заданной вероятности βi.
При фиксации величины βi детерминированный эквивалент (4) – (7) переходит в класс моделей линейного программирования (ЛП). Анализ модели ЛП осуществляется модифицированным симплекс-методом с мультипликативным представлением обратной матрицы.
Из-за относительно небольшой размерности (десятки переменных и ограничений) не требуется значительных затрат памяти ЭВМ и времени счета, что существенно упрощает практическую реализацию оптимизационной модели.
Литература:
- Юдин Д.Б. Математические методы управления в условиях неполной информации. – М.: Сов.радио, 1979.- 392с.
- Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях: Монография. Тюмень: Издательство Тюменского государственного университета, 2000. – 352 С.
- Первозванский А.А. Математические методы в управлении производством. – М.: Наука, 1975. – 616 с.
- Рахимов Т.Н. и др. Основы построения АСУ/Т.Н. Рахимов, О.А. Заикин, Б.Я. Советов; под общ. ред. Б.Я. Советова. – Т.: Укитувчи, 1984. – 376 с.

