Современная фрактальная теория: визуализация и прикладные аспекты



Современная фрактальная теория: визуализация иприкладные аспекты

Власов Дмитрий Анатольевич, кандидат педагогических наук, доцент

Российский экономический университет имени Г. В. Плеханова (г. Москва)

В центре внимания статьи — современная фрактальная теория, одно из перспективных направлений, используемых для анализа социально-экономических проблем и ситуаций. Представлены примеры визуализации фракталов в базе знаний и наборе вычислительных алгоритмов WolframAlpha, раскрыты прикладные аспекты фрактальной теории (исследовательские и методические аспекты).

Ключевые слова:фрактал, самоподобие, фрактальная теория, визуализация, WolframAlpha, циклические колебания, экономическая кибернетика

Происхождение термина «фрактал» связано с латинским словом fractus (разбитый, сломанный, дробленый). Основным свойством фрактала как математического множества является свойство самоподобия. Благодаря этому свойству целый объект имеет форму, аналогичную форме частей. Отметим существенный вклад французского и американского математика Бенуа Мандельброта, автора монографии «Фрактальная геометрия природы» как в создание фрактальной геометрии, так и в популяризацию фракталов. Новые информационные технологии WolframAlpha [1, 2, 9] предоставляют широкие возможности по визуализации геометрических структур в виде фракталов и предфракталов, изучении их необычных свойств.

К наиболее популярным фракталам, получаемым с помощью специальных рекурсивных процедур, относятся:

‒ кривая дракона (модификация Dragon curve; 1 итерация, 3 итерации, 10 итераций рис. 2);

‒ кривая Коха (Koch snowflake; 1 итерация, 2 итерации, 100 итераций, рис. 1);

‒ кривая Миньковского (модификация Minkovski sausage; 1 итерация, 2 итерации, 100 итераций рис. 1);

‒ кривая Пеано (модификация Peano curve; 1 итерация, 2 итерации, 4 итераций, рис. 2);

‒ кривая «Причудливый узор» (Сurlicue fractal; константа Pi, 1 итерация, 25 итерации, 100 итераций, рис. 2);

‒ кривая «Квадрат льда» (Square ice fractal; 1 итерация, 3 итерации, 25 итераций, рис. 1);

‒ кривая Леви; кривая Мякишева; кривая Гильберта; дерево Пифагора и др.

Мы считаем, что изучение различных свойств фракталов и фрактальных кривых должно найти отражение в системе целеполагания прикладной математической подготовки бакалавра [4].

Рис. 1. Примеры визуализации фракталов в WolframAlpha

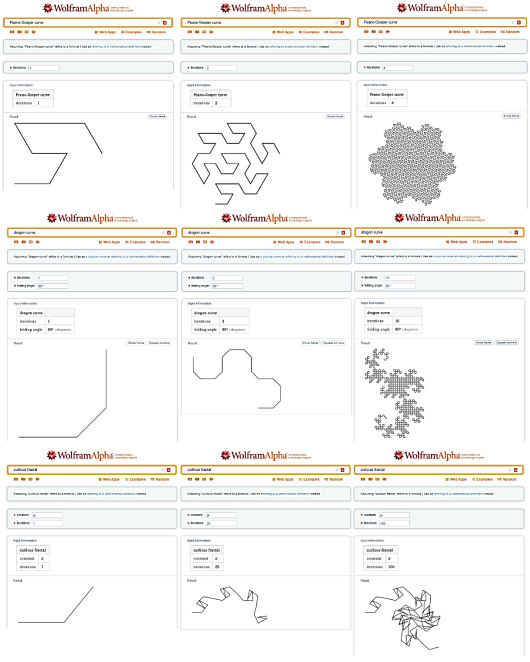
Рис. 2. Примеры визуализации фракталов в WolframAlpha

Одним из модных подходов к моделированию и прогнозированию экономики в последние годы стала фрактальная теория. Несмотря на попытки создания, однозначного математического определения понятия «фрактал» к настоящему времени не создано. Сейчас фрактал определяют как крайнюю непредсказуемость постоянного нелинейного и нерегулярного сложного движения, возникающую в динамической системе. Существенная зависимость от имеющихся начальных условий динамической системы объясняет своеобразную непредсказуемость фракталов. Именно благодаря этой зависимости одним из выводов фрактальной теории является невозможность предсказать будущее (как по причине существующих ошибок наблюдений и измерений, так и по причине неполноты информации о рассматриваемой экономической проблеме и ситуации). При этом именно современные экономические проблемы и ситуации составляют содержание прикладной математической подготовки бакалавра менеджмента [7] и бакалавра экономики [8].

Широкое применение фрактальной теории в экономике связано с исследованиями американского экономиста Чарльз Доу, раскрывшего новые механизмы функционирования финансовых рынков посредством введения в рассмотрение циклических колебаний [10].

В середине XX века американский экономист Ральф Эллиот обобщил теорию изменения цен на финансовые активы с использованием понятия «фрактал». Сегодня мы воспринимаем волновую теорию Эллиота как одну из классических теорий технического анализа финансового рынка. Заслуга Ральфа Эллиота в инструментальном применении достижений фрактальной теории с целью представления тенденции в виде системы из более мелких, понятных и поддающихся анализу компонентов, в рамках которых становится возможным технический анализ риска и доходности финансовых инструментов [11].

Однако существование и развитие фрактальной теории достаточно неоднозначно соседствует с классической наукой. В силу непредсказуемости фракталов в настоящее время есть возможность прогнозировать исключительно модель поведения исследуемой экономической системы (невозможно построить прогноз в классическом понимании, и следовательно, невозможно провести его проверку). На современном этапе развития экономической кибернетики [3] не существует полноценного инструментального применения фрактальной для исследования множества экономических проблем и ситуаций, поэтому настаивать на обязательном применении фрактальной теории нельзя. Наряду с этим, фрактальная теория является современным перспективным направлением прикладной математики с точки зрения исследования и визуализации разнообразных экономических проблем и ситуаций, в том числе в финансовой сфере [5], а WolframAlpha как развивающаяся системе предоставляет новые инструментальные возможности [6], способные существенно повысить уровень прикладной математической подготовки бакалавров.

Литература:

1. Власов Д. А. Возможности профессиональных математических пакетов в системе прикладной математической подготовки будущих специалистов // Вестник Российского университета дружбы народов. Серия: Информатизация образования. — 2009. — № 4. — С. 52–59.
2. Власов Д. А. Информационных технологии в системе математической подготовки бакалавров: опыт МГГУ им. М. А. Шолохова // Информатика и образование. — 2012. — № 3. — С. 93–94.
3. Власов Д. А. Особенности и математические основы современной экономической кибернетики // Техника. Технологии. Инженерия. — 2016. — № 2. — С. 4–7.
4. Власов Д. А. Особенности целеполагания при проектировании системы обучения прикладной математике // Философия образования. — 2008. — № 4. — С. 278–283.
5. Власов Д. А. Технология визуализации проблем и ситуаций финансовой сферы // Педагогика высшей школы. — 2016. — № 2. — С. 35–38.
6. Власов Д. А., Синчуков А. В. Новые технологии WolframAlpha при изучении количественных методов студентами бакалавриата // Вестник Российского университета дружбы народов. Серия: Информатизация образования. — 2013. — № 4. — С. 43–53.
7. Власов Д. А., Синчуков А. В. Прикладная математическая подготовка бакалавра менеджмента // Образование и воспитание. — 2016. — № 4. — С. 57–60.
8. Власов Д. А., Синчуков А. В. Принципы проектирования прикладной математической подготовки бакалавра экономики // Образование и воспитание. — 2016. — № 3. — С. 37–40.
9. Качалова Г. А., Власов Д. А. Технологии Wolframalpha при изучении элементов прикладной математики студентами бакалавриата // Молодой ученый. — 2013. — № 6. — С. 683–691.
10. Петерс Э. Фрактальный анализ финансовых рынков. — М.: «Интернет-трейдинг», 2004. — 304 с.
11. Тихомиров Н. П., Тихомирова Т. М. Риск-анализ в экономике. — М.: Издательство «Экономика». — 2010. — 318 с.