Методы проектирования радиолинз СВЧ и КВЧ-диапазона



В статье рассматриваются методы проектирования радиолинз как основных элементов диаграммообразующих схем антенных решеток радиоэлектронных систем СВЧ и КВЧ диапазонов. В рамках содержательной части представлен подход к использованию метода геометрической оптики при проектировании радиолинз. Проанализированы и обобщены альтернативные методы синтеза диэлектрических радиолинз, представлены особенности их использования в зависимости от различных целей, исходных данных и условий проектирования.

Ключевые слова: геометрическая оптика, СВЧ линза, асимптотические методы проектирования диэлектрических линз.

СВЧ линзы как диаграммообразующие схемы (ДОС) появились в 1950-х годах, и впоследствии получили многочисленные приложения. Достижения в материаловедении и технологии изготовления привели к новым направлениям реализаций СВЧ линз, использующих волноводы, полосковые и микрополосковые линии передач. В последние годы стали доминировать беспроводные коммуникации, поддерживающие многолучевые и адаптивные антенные решётки. Многие приложения, включая автомобильные радары, предотвращающие столкновения, дистанционно пилотируемые радары и спутниковые сенсоры различного назначения — всем им необходимы компактные, лёгкие антенные системы, способные обеспечивать достаточно большой угол сканирования в широком диапазоне частот. Развитие печатных СВЧ линз предполагает возможные технические, конструктивные решения для таких развивающихся технологий [1–3]. СВЧ линза является структурой, способной фокусировать электромагнитную энергию в точке. Радиолинзы делятся на замедляющие, в которых фазовая скорость распространения электромагнитной волны ниже скорости света, и ускоряющие. Замедляющие линзы выполняются из диэлектрика; в который вкраплены токопроводящие элементы. Ускоряющие линзы изготовляются из параллельных металлических пластин или секций прямоугольных волноводов. Наиболее широко используются многолучевые линзы, обеспечивающие широкий сектор излучения и приёма: сферические и цилиндрические линзы Люнеберга, линзы Ротмана и так называемые линзы R-2R.

Геометрическая оптика в проектировании СВЧ линз

Геометрическая оптика (GO) очень удобна при формализованном описании конструкции СВЧ линзы. Она вытекает из асимптотического решения уравнений Максвелла в высокочастотной области СВЧ-КВЧ диапазонов [4]. В пределах условия превышения длины волны габаритными размерами линзы и радиусом кривизны, поверхности распространения волны внутри однородной изотропной линзы могут удобно моделироваться в терминах элементарных лучевых трубок. Излучение исходит из фазового центра источника вдоль прямой линии, с амплитудой, взвешенной ДН источника и затуханием по длине пути обратно пропорционально квадратному корню поперечного сечения лучевой трубки, и с фазой, заданной длиной электрической цепи (рисунок 1) [5, 6]. Отражение и передача на поверхности происходят в соответствии с законами Снеллиуса, вытекающими из принципа Ферма [5], а амплитуда луча зависит от коэффициентов Френеля и коэффициента расхождения пучка.

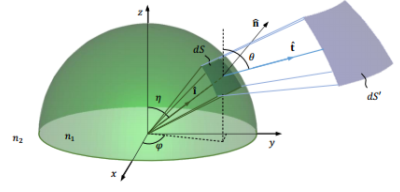
Рис. 1. Геометрия линзы и лучевой трубки при формализации в терминах GO

Если предположить, что границу раздела между двумя диэлектрическими средами можно рассматривать в пределах плоскости, отражение падающей плоской волны происходит в той же среде, с одинаковыми углами падения и отражения — закон Снеллиуса для отражения [1, 5]. Преломление регулируется законом Снеллиуса:

n₁sin(θ_inc) = n₂sin(θ_trans) (1)

где n₁ и n₂ — коэффициенты преломления каждой среды и θ_inc и θ_trans являются углами падения и прохождения, определяемыми по отношению к нормали к поверхности (рисунок 2). Если обе среды имеют одинаковую магнитную проницаемость, то n₁ = и n₂ = , где ε_r1 и ε_r2 — относительная диэлектрическая проницаемость каждого материала. Преломленная волна отклоняется в направлении нормали к поверхности, если волна входит в среду с высокой диэлектрической проницаемостью (рисунок 2, а), и она отклоняется от нормали при выходе из среды с более высокой диэлектрической постоянной (рисунок 2, б) [7].

Принимая во внимание, что в общем случае поверхность линзы имеет произвольную искривленную форму, хотя и с большим радиусом кривизны (по сравнению с длиной волны) в любой точке, то удобно представить уравнение (1) в более общем виде:

(2)

где и — векторы падающего и преломленного направления волновых чисел, соответственно (рисунок 1) и — вектор нормали к поверхности.

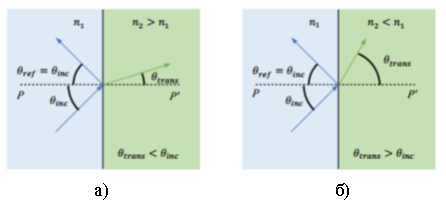
Рис. 2. Плоская волна, падающая на границу раздела между двумя диэлектриками: а) — отклонение из среды с низкой проницаемостью; б) — отклонение из среды с высокой проницаемостью.

Выражая эти три вектора в сферических координатах, размещённых в точке фазового центра облучателя, уравнение (2) для осесимметричной линзы принимает вид [6–8]:

, (3)

где r(η) представляет собой неизвестный профиль линзы, в то время как функция выходного угла θ(η) является другой неизвестной, устанавливаемой отдельными условиями проектирования, включающими фазу, или амплитуду или, в конечном счёте, поляризацию. Это условие может быть задано алгебраическим или дифференциальным уравнением. Система уравнений должна быть интегрирована в интервале η  [0, η_max] с использованием начальных условий r(0) и θ(0) и конечным значением η_max [7].

Если траектория луча включает участие других диэлектрических поверхностей, каждая из них должна соответствовать уравнению Снеллиуса, эквивалентному (3). Вторая поверхность линзы обеспечивает установление дополнительных характеристик ДН, которые переводят в соответствие уравнения с использованием радиуса r_n(η) поверхности n и угла выхода луча θ_n(η). Система всех включённых уравнений решается путём обобщения процедуры, представленной выше для одной поверхности [7, 8].

Характеристика многократных внутренних отражений становится сложной с увеличением числа линзовых оболочек [2], но в общем случае не существует значительных преимуществ во включении их влияния в процессе синтеза линз. Вместе с тем, постановка задачи проектирования должна включать коэффициенты пропускания, коэффициент дивергенции и потери на рассеивание в материале, где это происходит. Анализ внутреннего отражения может быть выполнен апостериори при оценке эффективности линзы.

Согласно литературным источникам, синтез линзы на основе GO используется для различных условий проектирования, начиная от задач простой коррекции фазы [8] или с дополнительными параметрами ослабления поля к краям раскрыва, до многолучевых или проблем сканирования луча [2, 3], или задач корректировки формирования луча заданной формы [6, 7]. Методы GO были применены для синтеза осесимметричной линзы, а также для произвольной линзы любой формы [3, 6], для линз с несколькими оболочками и неравномерным преломлением [9], или, фактически, для любой комбинации предыдущих случаев.

Точное решение для общих 3D структур с использованием GO включает количественную оценку параметров линзы [9, 10]. Метод возмущений, например, предложенный в [10] может быть реализован для определенных типов несимметричных целевых ДН и позволяет найти соответствующую форму для заданной несимметричной линзы. При необходимости, адаптация одного и того же принципа может быть использована для регулировки формы линзы для получения осесимметричного исходящего луча.

Другие методы проектирования СВЧ-линзы

Преимущество метода GO прямого синтеза, рассматриваемого в статье, заключается в том, что он обеспечивает форму линзы, удовлетворяющую требованиям к конструкции после первичной численной оценки аналитических выражений замкнутой формы, без необходимости каких-либо итераций проб и ошибок. Требуемые объём памяти и ресурсы процессора фактически незначительны в случае осесимметричных линз. Хотя GO прямого синтеза достаточно для большого количество приложений, метод является асимптотическим, действует в оптических границах, тем самым, пренебрегая дифракционными эффектами, которые становятся важными, при уменьшении размера линзы [11].

Альтернативные методы проектирования можно рассматривать, когда требуется более точное решение линзы для заданных характеристик диаграммы направленности антенной системы. Они, как правило, основаны на процессе проб и ошибок с участием параметризированной модели и метода анализа характеристик линзы. Точность конструкции зависит от точности численного моделирования и количества требуемых итераций, обусловленных имеющимися вычислительными ресурсами. Эффективность процесса проектирования во многом зависит от того, насколько продумана процедура оптимизации из-за проблем конкретных линз, которые предварительно детализируются. Использование GO прямого синтеза линзы в качестве первого приближения для итерационного процесса может повысить его эффективность.

Прежде чем описывать альтернативный итеративный метод проектирования СВЧ-КВЧ-линз, следует обобщить следующие положения:

1. Метод синтеза линзы в замкнутой форме (например, метод GO, описанный выше) начинается с перечня входных параметров и конструкторской спецификации и непосредственно обеспечивает соответствующую форму линзы, основанную на замкнутой форме описания, без применения итераций проб и ошибок. В этом значении метод можно дополнительно классифицировать как метод прямого синтеза. В целом, проверка характеристик линз требует последующего одноразового использования метода анализа линзы.
2. В методах итерационного синтеза линзы ее форма описывается некоторым аналитическим или численным представлением с неизвестными коэффициентами, определяемыми внутри итерационного цикла оптимизации, который проверяет каждую сгенерированную линзу с использованием соответствующего метода анализа линзы, пока методом проб и ошибок не будут достигнуты целевые характеристики или диаграммообразующей схемы, или антенной решетки (антенной системы).
3. Метод анализа линз предназначен для оценки эффективности проектируемого (существующего) резонатора, либо используя приближенный метод или электродинамический решатель. Его выходом являются характеристики, а не форма линзы.

В отличие от методов прямого синтеза, список доступных методов анализа значительно больше. Наиболее часто используемые методы, сгруппированные в соответствии с типом электромагнитного моделирования, представлены следующим образом [1, 12].

Асимптотические методы:

– геометрическая оптика / физическая оптика (GO/PO),

– физическая оптика / физическая оптика (PO/PO),

– метод спектральной области (SDM).

Электродинамическое моделирование:

– метод сферической волновой моды (Spherical Wave Modal Method),

– метод конечных элементов (FEM),

– метод моментов (MoM),

– метод конечных разностей во временной области (FDTD).

Особенности применения этих методов проектирования СВЧ линз можно представить следующим образом.

Гибридный метод GO/PO, считается одним из наиболее часто используемых подходов в анализе СВЧ–КВЧ линз. В качестве входных данных этот метод предусматривает форму линзы и диэлектрическую проницаемость материала, расположение облучателя, а также ДН дальнего поля облучателя, при погружении в неограниченную среду, имеющую ту же диэлектрическую проницаемостью, как у СВЧ–КВЧ линзы.

Процедура GO/PO включает два этапа. Вначале постановка в терминах GO, как описано выше, используется для вычисления распределения поля на внутренней поверхности линзы; затем используются коэффициенты Френеля для вычисления поля на внешней поверхности линзы. Когда одна или больше диэлектрических поверхностей пересекаются лучевыми трубками, возникающими в фазовом центре облучателя, должны быть использованы соответствующие коэффициенты Френеля и дивергенции [4, 5, 8].

Гибридный метод (PO/PO) также двухступенчатый, как и GO/PO, но теперь вычисление полей апертуры на первом этапе основано на постановке PO. Это позволяет обойти два ограничения GO:

– GO не может быть использован на первой стадии для небольших СВЧ–КВЧ линз, где облучатель уже не может быть точно представлен точкой и его ДН дальнего поля;

– GO не может предсказать поля вблизи каустики. Этот аспект становится критическим, когда каустика подходит к краю линзы, затрагивая правильную оценку дифракционных эффектов края, или когда каустика подходит к области облучателя, таким образом, существенно затрагивая импеданс облучателя [4].

Методы спектральной области (SDM) являются возможной альтернативой GO/PO при анализе интегрированной линзовой антенны. Он представляет особый интерес для небольших СВЧ–КВЧ-линз, размером только в несколько длин волн, где классический подход геометрической оптики терпит неудачу.

В методах SDM дальнее поле линзы определяется из разложения полей облучателя апертуры в основании линзы в заданных базисных функциях. Эти функции могут быть, например, плоскими волнами или гауссовыми пучками [2–4]. Основное преимущество гауссовых пучков состоит в том, что они оба ограничены пространственно и спектрально. Оценка поля в ближней зоне у основания СВЧ линзы требует использования другого метода, например, метода моментов [12]. Гауссово разложение представляет несколько параметров пучка, устанавливающих ширину луча, наклон, пространственное и спектральное разделение между базисными функциями.

В работах [6, 11] SDM в сочетании с методом трассировки лучей используется для анализа расширенной полусферической СВЧ линзы. Результаты сравниваются с электродинамическими коммерческими пакетами ПО и экспериментальными измерениями.

Метод сферической волновой моды основан на дискретности электромагнитного поля в группе базовых функций, которые являются решениями волнового уравнения в сферических координатах. Примеры такого подхода можно найти, например, в [2, 11, 13], для анализа сферической однородной или стратифицированной линзы Люнеберга.

Для каждого слоя линз, внутренние и внешние поля дискретизируются в сферических модах. Методика согласования мод (типов волн) используется для получения коэффициентов разложения. Априори, известны коэффициенты только для падающей волны на наружный слой линзы. Все остальные коэффициенты должны быть определены из наложения граничных условий на границах раздела слоёв. Применение граничных условий формирует ряд линейных уравнений, которые будучи однажды решенными, обеспечивают коэффициенты всех полей в каждой области.

Метод моментов (MоM) в анализе СВЧ–КВЧ линз относительно редко встречается в литературе. Причина, в какой-то мере, заключается в том, что связанная с MоM матрица линейных уравнений может иметь слишком громоздкий размер для больших электромагнитных объектов, в то время как СВЧ линзы, обычно являются большими в терминах длины волны [12].

В методе конечных разностей во временной области (FDTD), как и в МоМ, использование традиционных 3D FDTD как алгоритма итеративного анализа ограничивается СВЧ–КВЧ линзами с размерами, близкими к длине волны. Действительно, число переменных алгоритма возрастает в кубе с увеличением радиуса линзы, что приводит к слишком большим вычислительным затратам для наиболее распространенных задач оптимизации. Тем не менее, для структур с осевой симметрией, можно свести 3D к более простой 2D задаче и реализовать более быстрый алгоритм, называемый телом вращения (Body of Revolution, BOR) FDTD. BOR-FDTD можно использовать, даже если симметричная СВЧ линза запитана асимметричным источником [14]. В этом случае ток облучателя или его излучаемое поле может дискретизироваться в разложении Фурье. Каждый элемент разложения отдельно анализируется с помощью алгоритма BOR-FDTD, и конечный результат получается по векторной сумме всех частей BOR-FDTD анализа.

Метод BOR-FDTD может быть реализован для небольших СВЧ линз, где, например, не может быть использован метод GO/РО. Действительно, чем меньше СВЧ линза, тем быстрее BOR-FDTD будет сходиться к решению, так как число элементов пространства сетки уменьшается со снижением размера линзы. BOR-FDTD может обрабатывать внутренние отражения, так как он является электродинамическим методом, а также может быть реализован для многослойных или СВЧ линз с различной диэлектрической проницаемостью.

Следует отметить, что возможно рассмотрение двух альтернативных подходов в параметрическом моделировании СВЧ линзы. Полиномиальный тип представления может быть принят, когда коэффициенты являются неизвестными для оптимизации в цикле вместо большой совокупности координат поверхности СВЧ линзы. Это решение является достаточно гибким, допуская представление произвольных форм. Недостаток заключается в том, что алгоритм оптимизации может генерировать ненужное количество бесполезных форм линз, а не потому, что та или иная геометрия является невозможной, но потому, что случайно сгенерированные линзы могут легко создавать полное внутреннее отражение, поверхностные волновые моды и каустику, особенно для интегрированных многооболочных линз, которые могут быть обнаружены только после процесса анализа [2, 9].

При втором подходе [11], пространство поиска может быть сужено к конкретным классам линз с помощью аналитических профилей линз, полученных методом синтеза GO, но позволяя управлять рассматриваемыми параметрами с помощью алгоритма оптимизации. Аналитические решения с целью обеспечения электромагнитной жизнеспособности всех решений тестируются в итерационном процессе. Между этими двумя подходами существует компромисс времени сходимости решения и гибкости проектирования.

На рисунке 3 представлены описанные процедуры и рабочий процесс — инструмент анализа и оптимизации при проектировании СВЧ–КВЧ линз. Этот инструмент был реализован в пакете ПО (ILASHsoftware tool), разработанном в Instituto de Telecomunicações Португалии, для круговой формы интегрированных линзовых антенн с одинарным или двойным слоем, и может обрабатывать несколько определений целевых характеристик [15].

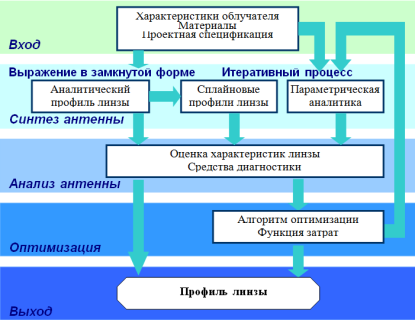
Рис. 3. Блок-схема этапов проектирования СВЧ–КВЧ линз

Метод анализа СВЧ-линзы основан на GO/PO, а оптимизация основана на метаэвристических, в частности, генетических алгоритмах.

Заключение

Таким образом, в статье показано, что приближенные методы проектирования радиолинз СВЧ–КВЧ диапазона связаны с задачами излучения и рассеяния электромагнитных волн. Их отличие от задач печатных или волноводных схем состоят в необходимости определения поля в области больших электрических размеров. Дискретизация больших областей порождает задачи большой размерности. Поэтому использование таких методов как FEM и FDTD заведомо неэффективно.

Более того, часто оказывается неэффективным существенно более экономичный метод моментов. В таких случаях строгие методы вычислительной электродинамики необходимо дополнить, так называемыми, асимптотическими или гибридными методами моделирования и проектирования радиолинз СВЧ–КВЧ диапазона.

Литература:

1. Кочетков В. А., Сивов А. Ю., Солдатиков И. В. и др. Современное состояние и возможные направления совершенствования элементов методологии проектирования линзовых антенных решеток РЭС СВЧ диапазона [Текст] / В. А. Кочетков, А. Ю. Сивов, И. В. Солдатиков, А. В. Тихонов, Н. В. Шишкин / Научно-технический журнал Информационные системы и технологии. № 5 (97) сентябрь — октябрь 2016 г. — Орел: ОГУ им. И. С. Тургенева, 2016. — С. 73–82.
2. Fuchs B., Palud S., Coq L. Le, Lafond O., Himdi M., Rondinean S. Scattering of spherically and hemispherically stratified lenses fed by any real source, «IEEE trans. Antennas and Propag., 2008. vol. 56, no. 2, pp. 450–460.
3. Zhang, Y., Christie, S., Fusco, V.: «Reconfigurable beamformimg using phase-aligned Rotman lens», IET Microwaves, Antennas and Propagation, 2012, vol. 6, no. 3, pp. 326–330.
4. Бреховских, Л. М. Волны в слоистых средах [Текст] / Л. М. Бреховских. — М.: Изд-во Академии наук СССР, 1957. — 502 с.
5. Сивухин Д. В. Общий курс физики. Учеб. пособие: для вузов в 5 т. Том IV. Оптика [Текст]. — 6-е изд. М.: Физматлит, 2015. — 656 с.
6. J. Dong, A. I. Zaghloul. Extremely high-frequency beam steerable lens-fed antenna for vehicular sensor applications. //IET Microw. Antennas Propag., 2010, vol. 4, pp. 1549–1558.
7. Кочетков В. А., Сивов А. Ю., Солдатиков И. В. и др. Применение методов геометрической оптики при проектировании линзовых антенных решеток (2-я часть цикла статей) [Текст, рисунок] / Кочетков В. А., Сивов А. Ю., Солдатиков И. В., Тихонов А. В., Шишкин Н. В., Лысанов И. Ю. / Научно-технический сборник «Техника радиосвязи». — 2017. — Вып. 1 (32). — Омск: ОНИИП, 2017. — С. 46–64.
8. Зелкин, Е.Г., Петрова, Р. А. Линзовые антенны [Текст] / Е. Г. Зелкин. — М.: Сов. Радио, 1974. — 280 с.
9. P. A. Belov and M. G. Silveirinha, Resolution of sub-wavelength lenses formed by a wire medium, Phys. Rev. E, 73, 056607, 2006.
10. Егоров А. А., Ловецкий К. П., Севастьянов А. Л., Севастьянов Л. А. Моделирование направляемых (собственных) мод и синтез тонкопленочной обобщенной волноводной линзы Люнеберга в нулевом векторном приближении // Квантовая электроника, 2010, том 40, № 9. — С. 830–836. Режим доступа: http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=qe&paperid=14332&option_lang=rus (дата обращения 08.01.2019).
11. John Thornton, Kao-Cheng Huang. Modern lens antennas for communications engineering. IEEE Press. Wiley, 2013. — 272 pages.
12. Кочетков В. А., Сивов А. Ю., Солдатиков И. В. и др. Структура областей применения численных методов моделирования линзовых антенных решеток СВЧ диапазона в процессе их проектирования (1-я часть цикла статей) [Текст] / Кочетков В. А., Сивов А. Ю., Солдатиков И. В., Тихонов А. В., Шишкин Н. В., Шеянов Д. Ю. / Научно-технический сборник «Техника радиосвязи». — 2016. — Вып. 3 (30). — Омск: ОНИИП, 2016.– С. 46–61.
13. Комарова, Е. В. Антенные и дифракционные характеристики многослойной линзы Люнеберга [Текст] / Е. В. Комарова / Автореферат дисс. на соискание ученой степени к. т.н. — Екатеринбург: ФГАОУ ВПО «Уральский федеральный университет им. Первого Президента России Б. Н. Ельцина», 2012. — 20 с.
14. Jun Shibayama, Bungo Murakami, Junji Yamauchi, Hisamatsu Nakao. LOD-BOR-FDTD Algorithm for Efficient Analysis of Circularly Simmetric. IEEE Microwave and Wireless Components Letters. Vol. 19, Issue: 2, Feb. 2009. Режим доступа: http://ieeexplore.ieee.org/document/4773156 (дата обращения 09.01.2019).
15. Eduardo Lima, Jorge R. Costa, Mario G. Silveirinha, Carlos A. Fernandes. ILASH — Software tool for the design of integrated lens antennas. 2008 IEEE Antennas and Propagation Society International Symposium (5–11 July 2008). Режим доступа: https://ieeexplore.ieee.org/document/4619133 (дата обращения 09.01.2019).