В современном мире каждый ученик ежедневно находится в огромном потоке информации. В подобных условиях от учителя требуется мастерство и творческое начало, чтобы поддерживать у школьников устойчивый интерес к знаниям и учёбе. Мотивация обучения алгебре и геометрии является одной из актуальных проблем методики преподавания в средней школе. Нестандартные формы урока — одно из средств разрешения этой проблемы, ведь необычное всегда кажется интересным.
В рамках традиционного урока трудно реализовать ряд задач. Например, добиться стойкой мотивации изучения предмета у большинства учащихся; трудно организовать работу с такими мыслительными операциями как сравнение, обобщение, классификация, анализ, синтез и т. д.; сложно показать межпредметные связи и их применение при решении различных задач.
Интегрированный урок с применением современных технологий позволяет добиться более качественных результатов обучения. Развитие устойчивого познавательного интереса, создание творческой атмосферы на уроке, элементы исследовательской деятельности позволяют углубить теоретические знания и развить практические навыки учащихся.
Использование на уроках игровых технологий обеспечивает достижение единства эмоционального и рационального в обучении. Во время математической игры происходит одновременно игровая, учебная и трудовая деятельность, расширяются возможности для решения воспитательных задач.
Мне хотелось бы поделиться опытом проведения интегрированного урока повторения, закрепления умений, систематизации и обобщения знаний. Урок проводится в 8 классе, после изучения раздела по алгебре «Рациональные дроби» и по геометрии «Четырехугольники».
Урок повторения и обобщения знаний наряду с интеграцией позволяет применять игровую и групповую форму учебной работы. Разные группы учащихся могут включаться в выполнение различных заданий с той целью, чтобы потом полнее осветить разные вопросы ранее изученного материала. При такой организации учебной работы школьники убеждаются в преимуществе коллективных форм учебной деятельности. На этих уроках восстанавливаются знания, предупреждается забывание. Их развивающая функция проявляется через способы анализа, систематизации материала. Воспитательные задачи решаются не только через методы, содержание учебного материала, но и через организацию коллективной деятельности учащихся.
Форма урока позволяет включать задачи творческого характера, дающие возможность по-новому взглянуть на ранее изученное.
Применяемые на уроке технологии:
– Технология учебно-игровой деятельности.
Игровая форма взаимодействия педагога и учащихся реализуется через определенный сюжет (игру). При этом образовательные задачи включаются в содержание игры.
– Технология дифференцированного обучения.
Использование данной технологии позволяет дифференцированно работать со всеми учащимися, не усредняя уровень знаний обучающихся, позволяя слабому видеть перспективу успеха, а сильному — иметь возможность творческого роста. Ученик становится субъектом процесса обучения.
– Технология группового обучения
Групповая технология предполагает: взаимное обогащение учащихся в группе, организацию совместных действий, распределение операций, ролей, развитие коммуникативных компетенций, обмен способами действия, взаимопонимание, рефлексия по принципу объединения школьников разного уровня обученности, совместимости, что позволяет им работать комфортно и дополнять знания друг друга.
– Здоровьесберегающие технологии
Реализации здоровьесберегающих технологий на уроке способствуют следующие приемы: смена видов деятельности, игровые приемы, физкультминутки.
Постановка целей урока.
Учитель: Сегодня у нас обобщающий урок, объединяющий две темы: по алгебре «Рациональные дроби» и по геометрии «Четырехугольники». Мы с вами вспомним и обобщим основные понятия, систематизируем знания, полученные по данным темам. Урок пройдет в виде- виде игры «Своя игра», с использованием презентации.
Комментарии корганизации игры.
Чтобы показать насколько занимательной может быть математика, мы разбились на две команды, условно названные «А» и «В». Игра состоит из трех раундов. В каждом раунде две темы и три уровня сложности. Команды будут по очереди выбирать тему и уровень сложности вопроса, обсуждать вопрос, принимать решение и поднимать сигнальный флажок. Если команда затрудняется с ответом, то право ответа может перейти к другой команде. У нас есть две команды болельщиков, которые будут также участвовать в игре и смогут принести своим командам дополнительные балы.
Ход игры
1 раунд
Выбираем категорию:
|
Найди лишнее |
10 |
20 |
30 |
|
Основные понятия |
10 |
20 |
30 |

Пока жюри подводит итоги у нас физкультминутка
Физкультминутка
Я буду называть утверждение из алгебры или геометрии.
Если вы считаете его верным, то выполняете следующее движение:
– одна рука вытягивается вдоль тела, а другая подносится к голове (как бы приветствуя верное утверждение).
Если вы считаете утверждение неверным, то
– вы кладете руки на пояс.
Итак:
– Если диагонали параллелограмма равны, то этот параллелограмм прямоугольник. (ДА)
– Гипербола является графиком линейной функции. (НЕТ)
– Если выражение не содержит деление на выражение с переменной, то оно называется целым. (ДА)
– Диагонали ромба являются биссектрисами его углов. (ДА)
– При умножении рациональных дробей первую дробь умножают на дробь, обратную второй. (НЕТ)
– Прямоугольник, у которого все стороны равны, называется квадратом. (ДА)
– Диагонали квадрата перпендикулярны. (ДА)
Слово для подведения итогов 1-ого раунда предоставляется жюри.
2 раунд
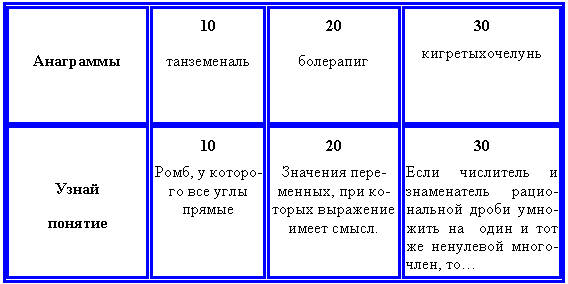
Выбираем категорию:
|
Анаграммы |
10 |
20 |
30 |
|
Узнай понятие |
10 |
20 |
30 |
Пока жюри подводит итоги 2 раунда у нас конкурс болельщиков.
Конкурс болельщиков
Команды болельщиков вытягивают по очереди по два вида четырехугольников (параллелограмм, прямоугольник, ромб, квадрат). А затем они должны назвать каждую из фигур, дать ей определение, перечислить ее свойства. Правильный ответ по каждой из фигур добавит в копилку командам по 3 балла.
Слово для подведения итогов 2-ого раунда предоставляется жюри.
3 раунд
Выбираем категорию:
|
Задачи по геометрии |
10 |
20 |
30 |
|
Задания по алгебре |
10 |
20 |
30 |

Слово жюри для подведения итогов.
Учитель: Спасибо за урок. Все молодцы! В нашей игре нет побежденных. Победила математика. Мы убедились, насколько она может быть занимательной. Вы продемонстрировали свою дружбу с ней. Спасибо!
Приведенный выше урок позволяет решить следующие задачи:
Образовательные:
– Контроль знаний;
– Способствовать прочному усвоению учащимися учебного материала;
– Мотивация учебной деятельности
– Расширение кругозора учащихся и др.
Развивающие:
– Развивать у учащихся творческое мышление;
– Способствовать практическому применению умений и навыков, полученных на уроках и внеклассных занятиях;
– Способствовать развитию воображения, фантазии, творческих способностей и др.
Воспитательные:
– Способствовать воспитанию саморазвивающейся и самореализующейся личности;
– Воспитать нравственные взгляды и убеждения;
– Воспитание сотрудничества и коллективизма;
– Способствовать воспитанию самостоятельности и воли в работе и др.
Математическая игра позволяет органично соединить игровые и познавательные мотивы, и в такой игровой деятельности постепенно происходит переход от игровых мотивов к учебным мотивам. Игра помогает закреплять и расширять предусмотренные школьной программой знания, умения и навыки.
Сбалансированное применение современных образовательных технологий позволяет активизировать познавательный интерес учащихся, развивать их творческие способности, стимулирует умственную деятельность, а так же побуждает к исследовательской работе. Все это в конечном итоге способствует решению основной задачи стоящей перед современным учителем — воспитание активно мыслящей личности.
Литература:
- Данилюк А. Я., Кондаков А. М., Тишков В. А. Концепция духовно-нравственного развития и воспитания личности гражданина России. — М.: Просвещение, 2009. — 24 с. (Стандарты второго поколения).
- Примерные программы по учебным предметам. Математика. 5–9 классы: проект. 3-изд. перераб.– М.: Просвещение, 2011.– 64 с.
- Михайленко Т. М. Игровые технологии как вид педагогических технологий / Т. М. Михайленко // Педагогика: традиции и инновации: материалы междунар. науч. конф. (г. Челябинск, октябрь 2011 г.).Т. I. — Челябинск: Два комсомольца, 2011. — С. 140–146.
- Алгебра. Дидактические материалы. 8 класс /В. И. Жохов, Ю. Н. Макарычев, Н. Г. Миндюк.-М.:Просвещение,2014–160 с.
- Ершова А. П., Голобородько В. В., Ершова А. С. Самостоятельные и контрольные работы по алгебре для 8 класса.-М.: Илекса, 2015.
- Тесты по геометрии: 8 класс: к учебнику Л. С. Атанасяна и др. “Геометрия. 7–9” / А. В. Фарков. — 7-е изд., стереотип. — М.: Издательство “Экзамен”, 2014.
- Контрольно- измерительные материалы. Алгебра.8 класс / сост.В. В. Черноруцкий.- М.: ВАКО,2013.

