Организация творческой познавательной деятельности на занятиях кружка «Занимательная математика»



В соответствии с требованиями Федерального государственного образовательного стандарта второго поколения основного общего образования внеурочная деятельность стала важным составляющим учебного процесса. Предлагаемый материал содержит примерные разработки занятий кружка «Занимательная математика». Предназначен для обучающихся 5-х классов (10–11 лет).

Внеурочная деятельность по математике создает возможность разностороннего раскрытия индивидуальных способностей школьников, развития интереса к углубленному изучению данной дисциплины, желания активно участвовать в продуктивной деятельности, умения самостоятельно организовать свое свободное время.

Цель кружка : создание условий, обеспечивающих интеллектуальное развитие личности школьника на основе развития его индивидуальности; создание фундамента для математического развития, формирование механизмов мышления, характерных для математической деятельности.

Реализация занятий осуществляется с использованием электронного обучения, дистанционных образовательных технологий.

Задачи кружка:

Обучающие: расширение и углубление знаний по предмету;

Воспитывающие: пробуждение и развитие устойчивого интереса учащихся к математике и ее приложениям, расширение кругозора;

Развивающие : развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой;

Дополнительные задачи решаемые данными внеурочными занятиями:

– раскрытие творческих способностей учащихся;

– воспитание твердости в пути достижения цели (решения той или иной задачи);

– решение специально подобранных упражнений и задач, направленных на формирование приемов мыслительной деятельности;

– формирование потребности к логическим обоснованиям и рассуждениям;

– специальное обучение математическому моделированию как методу решения практических задач;

– работа с одаренными детьми в рамках подготовки к предметным олимпиадам и конкурсам.

Кружок ориентирован на 34 учебных часа (по 1 часу в неделю), срок реализации сентябрь — май.

Формы работы в рамках реализации кружка — комбинированное тематическое занятие:

– Выступление учителя или кружковца.

– Самостоятельное решение задач по избранной теме.

– Разбор решения задач (обучение решению задач).

– Решение задач занимательного характера, задач на смекалку, разбор математических софизмов, проведение математических игр и развлечений.

– Ответы на вопросы учащихся.

Значительная часть работы с обучающимися отводится практическим занятиям:

– Конкурсы и соревнования по решению математических задач, олимпиады, игры.

– Разбор заданий городской (районной) олимпиады, анализ ошибок.

– Изготовление моделей для уроков математики.

– Чтение отрывков из художественных произведений, связанных с математикой. Собственное написание рассказов и сказок с математическим содержанием

– Просмотр видеофильмов по математике.

На занятиях кружка большое внимание уделяется обсуждению различных модулированных ситуаций, групповым дискуссиям, ролевому проигрыванию, творческому самовыражению, самопроверке и формированию навыков умения выступать перед аудиторией.

Перечень отобранных для рассмотрения на занятии задач создается педагогом, как правило, ведущем учебный предмет у данных учащихся. Учитель знает уровень базовой математической подготовки, мотивации и потенциальной одаренности ребят. Обширный список специальной литературы из разных источников, включая интернет-ресурсы, позволяет педагогу включать в занятие разнообразные задачи, сообразно интересам и потребностям учащихся.

Материалы к занятию кружка. Тема: Действия с натуральными числами. Измерение отрезков.

Ниже приведена примерная схема одного из первых занятий кружка. Согласно календарно тематическому планированию в этот момент учащиеся на уроках повторяют действия с натуральными числами, решают задачи на простейшие геометрические построения (прямая, отрезок, его измерение, луч). Подбор заданий сделан с учетом данной тематики. Учитывая возраст кружковцев, занятие проходит в игровой форме.

Учитель: Здравствуйте ребята! Сегодня на уроке мы отправимся с вами на поиски математического клада на автобусе, а нашими экскурсоводами будут Незнайка и Знайка.

(на экране проектора автобус, сказочные герои Незнайка и Знайка)

Устный счет.

Учитель:Итак, прежде чем отправиться на поиски, Знайка предлагает вам задание.

Слайд:

300+ 200 =

450+150 =

340–140 =

550–550 =

850–450 =

980–180 =

300 + 400 =

Расставьте числа в порядке возрастания, и вы узнаете, что вам хочет пожелать Знайка!

0	200	400	500	600	700	800
У	С	П	Е	Х	А	!

Учитель:Мы прибываем на станцию «Смекалистых»

Ответьте, пожалуйста, на вопросы Знайки:

—У стола отпилили один угол. Сколько углов у него теперь? (5)

— В тарелке лежали три морковки и четыре яблока. Сколько фруктов было в тарелке? (4)

—У кошки Мурки родились щенята: один черненький и два беленьких. Сколько щенят у Мурки? (0)

— Прилетели два чижа, два стрижа и два ужа. Сколько стало птиц всего возле дома моего? (4)

—Один банан падает с елки каждые 5 минут. Сколько их упадет за один час? (0)

—На столе стояло 5 стаканов ягод. Миша съел один и поставил его на стол. Сколько стаканов стоит на столе? (5)

—Что случится с красным платком, если его опустить на дно моря на 5 минут? (намокнет)

Учитель:Мы прибыли на станцию «Спортивная». Вы знаете, что числа бывают четные и нечетные. Приведите примеры. Слайд.

Если я называю четные числа, то вы встаете, нечетные — сидите на месте.

2, 5, 7, 6, 8, 3, 10.

Физкультминутка.

Учитель: А сейчас вместе с Незнайкой сделаем зарядку.Слайд: сказочные герои занимаются спортом

Я скажу несколько математических предложений. Если предположение верное, то вы сидите, если оно ложное, вы встаёте, а кто-то из вас объясняет, почему оно ложное.

1. В записи числа «одна тысяча» три нуля.
2. В записи числа «один миллион» пять нулей.
3. Для записи натуральных чисел употребляются одиннадцать цифр.
4. Последующее натуральное число отличается от предыдущего на единицу.
5. У прямой есть два конца.
6. Число, получающееся при сложении чисел, называется разностью.
7. Уменьшаемое больше вычитаемого.

Учитель: Мы на станции Историческая

(Сообщение может сделать один из учащихся, после предварительной подготовки. Выступление сопровождается слайдами с изображением линеек разного вида)

В 2019 году у линейки юбилей. Ей исполнилось 230 лет. Однако линейки использовались и в более ранние времена. В Средневековье, например, немецкие монахи для разметки линий на листках пергамента пользовались тонкими свинцовыми пластинками. А в ряде стран Европы, в том числе и в Древней Руси, для этих целей применялись железные прутья. Их называли шильцами. В разных странах люди измеряли одно и то же расстояние по-разному. Это было очень неудобно.

Наконец, во Франции в 1789 году решено было ввести единую систему мер. В Париже изготовили платиновые линейки с делениями, которые стали образцами мерок для всего мира. По их образцу изготовили деревянные линейки для остальных. В Россию линейка попала после войны 1812 года в качестве военного трофея. Этой системой измерения мы пользуемся, и по сей день

Учитель: решим задачу, в который приведены длины отрезков, измеренные той самой линейкой, о которой мы узнали так много интересного.

Задача (текст выведен на экран):

В треугольнике DKC сторона DK меньше стороны KC на 6 см и больше стороны DC на 2 см. Найдите периметр треугольника DKC, если DC = 18 см.

(DK = 18 + 2 = 20 см, KC = 20 + 6 = 26 см, P = DK + KC + DC = 20 + 26 +18 = 64 см).

Учитель: Мы на станции Сказочная

Задачи бабы Яги. На экране избушка на курьих ножках, тексты задач на разных слайдах

1. У меня в лесу есть участок, где я выращиваю елочки специально для новогодних праздников. Этот участок имеет прямоугольную форму, Е го ширина 200 м, и это на 50 м меньше длины. Найти периметр участка
2. Когда Василисе Премудрой исполнилось 18 лет, Кощей Бессмертный решил взять ее замуж. Василиса спросила, сколько у Кощея сундуков с золотом. Кощей сказал, что у него 300 сундуков, полных золота, и каждый год прибавляется еще по 2 сундука. Василиса обещала выйти замуж за Кощея тогда, когда у него будет 500 сундуков, полных золота. Сколько лет будет невесте Кощея в день свадьбы?

Решение: Невесте будет 118 лет.

Учитель: не захотел Кощей Бессмертный так долго ждать Василису, он решил жениться на дочке Бабы Яги- на Акулине. Только пусть она сначала научится читать, писать, считать. Сейчас она как раз выполняет домашнее задание по математике.

Проверьте вычисления Акулины (слайд)

100×25=240 (2500);

891000:2700=230 (330)

Учитель: Молодцы! Исправили ошибки! Знайка вами очень доволен (Слайд с улыбающимся Знайкой)! А сейчас вам пора домой. Делать уроки и стараться не допускать ошибок! До новых встреч!

Материалы к занятию кружка. Тема: «Решение уравнений»

Занятие целесообразно провести параллельно с изучением данной темы в классе или при повторение изученного материала.

Занятие проходит в форме командной игры.

Ведущий: когда уравненье решаешь дружок,

Ты должен найти у него корешок.

Значение буквы проверить не сложно,

Поставь в уравненье его осторожно.

Коль верное равенство выйдет у вас,

То корнем значенье зовите тот час.

Конкурс № 1

1 этап: ответить на вопросы:

1. 1 команда: что называется уравнением?
2. 2 команда: что называют корнем уравнения?
3. 3 команда: что значит решить уравнение?

2 этап: на доске записаны 3 вида уравнений в общем виде. Нужно записать, как найти неизвестное.

1 команда: x + a = b x =

2 команда: x — a = b x =

3 команда: b — x = a x =

3 этап: дать словесную формулировку нахождения неизвестного в предложенном уравнении каждой команде.

Конкурс № 2

Составить уравнение по условию задачи и решить её.

1. 1 команда: от сосиски длиной 72 метра живущей на мясокомбинате пёс отъел кусок, осталось всего 45 метров. Сколько метров сосиски отъел пёс, живущий на мясокомбинате?
2. 2 команда: в корзине было несколько яблок. После того, как в неё положили ещё 15 яблок, в ней стало 42 яблока. Сколько яблок было в корзине?
3. 3 команда: у девочки было некоторое количество денег. После того, как она купила своему любимому попугаю Гоше корм на 63 рубля, у неё осталось ещё 35 рублей. Сколько денег было у Гошиной хозяйки в самом начале?

Минутка отдыха . Фокус: отгадывание задуманного числа.

Задумайте любое число, умножьте его на 2, прибавьте 1, полученный результат увеличьте в 5 раз, вычтите 4, умножьте на 2. Что у вас получилось? (Если от названного числа отнять 2, а затем полученное число разделить на 20, то получим задуманное число.)

Конкурс № 3

Творческое задание. Командам предложены уравнения:

1. 1 команда: (х –35) –18 = 17;
2. 2 команда: 12 + (х + 34) = 83;
3. 3 команда: 93 — (х + 56) = 8.

Необходимо составить задачу по данному уравнению, решить её.

Конкурс № 4

Решение задачи с помощью уравнения:

На одной чаше весов лежат 6 одинаковых яблок и 3 одинаковые груши, на другой чаше- 3 таких же яблока и 5 таких же груш. Весы находятся в равновесии. Что легче : яблоко или груша?

Материалы к занятию кружка. Тема: «Умножение натуральных чисел»

1)Игра «Верю — не верю».

1. Числа, которые перемножают, называют множителями. (да)
2. Выражение называют суммой. (нет)
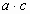
3. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. (да)
4. При умножении числа на единицу получиться то же самое число. (да)
5. Числа, которые делят, называют множителями. (нет)
6. Если один множитель увеличить в 2 раза, а другой в 5 раз, по произведение увеличиться в 7 раз. (нет)
7. Если среди множителей есть нуль, по произведение равно нулю. (да)
8. Чтобы найти во сколько раз одно число больше другого, нужно выполнить вычитание. (нет)

2)Устная работа

1. Найдите значение выражений:

50 × 786 × 2

79 × 125 × 8

3×2×5

7×25×4

20×17×5

125×7×8

16×25×4

12×8∙×125

40×9×25

2. Вычислить

9999+9999+9999+9999+5.

3. Задача.

Ежедневно из бочки брали по 7 л воды. Через 9 дней в бочке осталось 37 л. Сколько литров воды было в бочке первоначально?

3)Олимпиадная задача.

Рот Буратино 1 метр, а длина его носа раньше была 9 сантиметров. Каждый раз, когда Буратино врал, длина его носа удваивалась. Как только нос стал длиннее самого Буратино, тот врать перестал. Сколько раз врал Буратино?

— Что значит «удваивалась»?

— Сколько сантиметров в 1 метре?

(Дети решают задачу самостоятельно в парах)

9 × 2 = 18

18 × 2 = 36

36 × 2 = 64

64 × 2 = 128

128 >100

Ответ: Буратино врал 4 раза.

4) Расшифровать

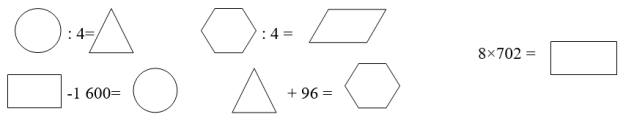
Решение практико-ориентированных задач

1. Для нормального протекания физиологических функций человеку в среднем требуется 3 л воды в сутки (с учетом поступления воды с пищевыми продуктами). Человек выпивает примерно 1л 500 мл воды, а остальное получает с пищевыми продуктами. Сколько литров воды потребуется человеку в месяц? за год?

Решение:

1. 1500 × 30 = 45 000 мл = 45 л — требуется выпить человеку за месяц.
2. 45000×12=540000 мл=540л-– требуется выпить человеку за год.

2.Однажды во время наводнения затопило подвал дома на набережной. Из подвала нужно было выкачать воду. Спасатели установили 5 больших и 3 малых насоса. Большой насос выкачивает за 1 час 4537 литров воды, а малый — 2120 литров. Через 6 часов вся вода была выкачана. Сколько литров воды скопилось в подвале во время наводнения? (Решите задачу 2 способами: по действиям; выражением).

Решение:

1. 5 × 4537 = 22685(л) — 5 б. насосов за 1 час.
2. 3 × 2120 6360 (л)– 3 м. насосов за 1 час.
3. 22685 + 6360 = 29 045 (л) всего за час.
4. 29045 × 6 = 174270 (л) скопилось в подвале во время наводнения.

3.Сердце человека перекачивает за сутки 8т. крови. Сколько тонн крови сердце перекачивает за 1 год? За 75 лет?

Решение.

1) 365*8=2920(т) — сердце перекачивает за год.

2) 2920*75=219000(т) — сердце перекачивает за 75 лет.

Ответ:219000тонн.

Приведенные примеры заданий и форм кружковой работы придают разнообразие проводимым занятиям, прививают интерес к предмету. Учащиеся учатся воспринимать математику не как скучную догму, а как увлекательную, живую, полезную в жизни науку.

Работа кружка выполняет познавательные и воспитательные функции. Ученики применяют приобретенные знания, открывают новые приемы и способы решений, рассуждений; развивается логическое мышление, развивается смысловая и образная память, формируется умение работать с нестандартными задачами. Ученики с огромным удовольствием показывают свои умения и навыки.

Внеурочная деятельность позволяет развить у учащихся личностные и метапредметные результаты: ребенок учится умению работать с информацией, ставить проблему и решать её, рассуждать при решении логических задач, задач на смекалку, на эрудицию и интуицию, систематизировать данные в виде таблиц при решении задач, при составлении математических кроссвордов, шарад и ребусов. Также становится настойчивым в достижении цели, способным принимать самостоятельные решения, приобретает навыки сотрудничества. Все это является ценнейшим багажом для успешного жизненного пути.