Данное учебно-методическое пособие содержит материал, расширяющий границы учебника, а также дополнительные сведения, необходимые для учащихся и учителя в их совместной деятельности. Особое место отводится методическим рекомендациям по изучению решения уравнений и неравенств данной темы, даются указания по работе с ними (алгоритм) и решения наиболее трудных из них с подробной записью преобразований. Изложение материала ведется с соблюдением примерного планирования учебного материала. Включены задания для самостоятельного решения.
Цели:
− Главная цель — развить навык в решении показательных уравнений и неравенств, предусмотренных уровнем обязательной подготовки.
− Увеличить объём умений и навыков за счёт упражнений «нового» типа.
− Продемонстрировать образцы логических приёмов для запоминания и воспроизведения учащимися.
− «Вооружить» путями поиска решений для дальнейшей самостоятельной работы, обеспечить эффективную организацию этой работы с учётом индивидуальных способностей и уровня математической подготовки учащихся.
− Активизировать познавательную деятельность учащихся для творческого применения полученных знаний в новых условиях так, чтобы учащиеся смогли обобщить и перенести данные приёмы и алгоритмы на изучение других разделов курса математики.
- Общий вид показательных уравнений. Характеристика. Теоремы.
Показательными уравнениями называют уравнения вида:af(x) = ag(x) (ах = аb), где а > 0, а ≠1, х — неизвестноеиуравнения, сводящиеся к этому виду (неизвестное содержится в показателе степени).
Рассмотрим и решим простейшие показательные уравнения графическим способом:
a) 2x = 1
b) 2x = 4
c) 2x = 8
d) 2x = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
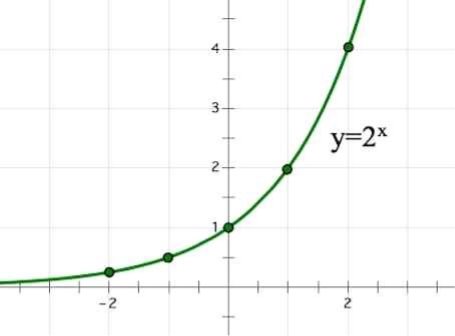
Решение:
a) Построив в одной системе координат графики функций y = 2x и у = 1, замечаем, что они имеют одну общую точку (0;1).
Значит, уравнение 2x = 1 имеет единственный корень х=0.
Итак, из уравнения 2x = 20 мы получили х=0.
b) Построив в одной системе координат графики функций y = 2x и у = 4, замечаем, что они имеют одну общую точку (2;4).
Значит, уравнение 2x = 4 имеет единственный корень х=2.
Итак, из уравнения 2x = 22 получили х=2.
c) и d) Исходя из тех же соображений, делаем вывод (теперь для отыскания корня графики можно и не строить).
2x = 8 и 2 x = ![]() , т. к.
, т. к. ![]() =
= ![]() =
= ![]()
2x = 23 2x = 2–4
х = 3 х = -4
В основе всех выводов при решении уравнений лежало свойство монотонности (возрастания) функции y = 2x и теоремы о единственности корня.
В указанной инструкции (самостоятельно) рассмотрите решение уравнений:
a) ![]() = 1
= 1
b) ![]() = 3
= 3
c) ![]() = 9
= 9
d) ![]() =
= ![]()
Убедитесь, чторешениями будут следующие числа:
a) х= 0
b) х= -1
c) х= -2
d) х= 2
В данных примерах выводы сделаны на основе свойства монотонности (убывания) функции y = ![]() итеоремы о единственности корня. Этот метод решения уравнений называется функционально-графический. Он основан на использовании графических иллюстраций:
итеоремы о единственности корня. Этот метод решения уравнений называется функционально-графический. Он основан на использовании графических иллюстраций:
1) построить графики функций левой и правой частей уравнения;
2) найти общую точку пересечения графиков.
Убедитесь самостоятельно, что уравнение вида: 2x = -4 не имеет корней.
Следовательно, мы убедились в справедливости двух теорем:
Теорема 1: Если а > 1, то равенство аt = аsсправедливо тогда и только тогда, когдаt=s.
Теорема 2: Если 0 < а < 1, то равенство аt = аsсправедливо тогда и только тогда, когдаt=s.
Опираясь на теоремы 1 и 2 мы можем сформулировать следующее утверждение:
Теорема: Показательное уравнение af(x) = ag(x) (где а > 0, а≠ 1) равносильно уравнению ![]() (x) = g(x).
(x) = g(x).
Приведём примеры:
Пример 1. Решить уравнения:
a) 22х-4 = 64
Решение:
Представим 64 как 26, перепишем заданное уравнение в виде:
22х-4 = 26
Это уравнение равносильно уравнению
2х— 4 = 6
2х = 6 + 4
2х = 10
х = 5
Ответ: 5
b) 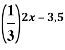 =
= ![]()
Решение:
Представим ![]() через степень числа
через степень числа ![]() :
:
![]() =
= ![]() =
= ![]() =
= ![]()
получим:
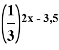 =
= ![]()
Это уравнение равносильно уравнению:
2х— 3,5 = 0,5
2х = 0,5 + 3,5
2х = 4
х = 2
Ответ: 2
c) ![]() =
= ![]()
Решение:
Заданное уравнение равносильно уравнению:
х2–3х = 3х— 8
Далее имеем:
х2–3х— 3х + 8 = 0
х2–6х + 8 = 0
D = b2–4ac; D = 36–32 = 4
![]() =
= ![]() ;
; ![]() =
=![]()
![]() =
= ![]() ;
; ![]() =
= ![]()
![]() =
= ![]() ;
; ![]() =
= ![]()
Ответ: 2; 4.
Пример 2. Решить уравнения:
a) ![]() = 1
= 1
Решение:
Необходимо уравнять основания. Мы знаем, что ![]() = 1.
= 1.
Получаем:
![]() =
= ![]()
![]() + 2x— 3 = 0
+ 2x— 3 = 0
D = 4–4 ∙ 1 ∙ (-3) = 0
![]() =
=![]() = 1
= 1
![]() =
=![]() = -3
= -3
Ответ: -3; 1.
b) 16 ∙ ![]() =
= ![]()
Решение:
Так как уравнение содержит корень четной степени, необходимо определить ОДЗ.
ОДЗ: x + 1 ≥ 0
x ≥ -1
Преобразуем левую часть по свойствам степеней:
![]() ;
; ![]()
16 ∙ ![]() =
= ![]()
Получаем: ![]()
Затем:
![]()
Решая это иррациональное уравнение, получаем:
![]()
![]()
![]()
![]()
![]()
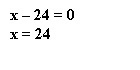
![]()
x = 0 или
Проверка:
Если x = 0;
116 ∙ ![]() =
= ![]()
![]()
![]() — равенство неверное;
— равенство неверное;
x = 0 — посторонний корень.
Если x = 24;
16 ∙ ![]() =
= ![]()
![]()
![]() — равенство верное.
— равенство верное.
Исходному уравнению удовлетворяет только значение x = 24.
Ответ: 24.
c) 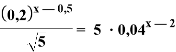
Решение:
В этом уравнении есть возможность и левую и правую части представить в виде степени с основанием 5.
− ![]() =
= 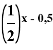 =
= ![]()
− ![]()
− 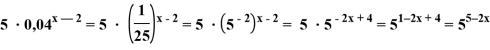
Заданное уравнение приобретает вид:
![]()
—![]()
![]()
x = 5
Ответ: 5.
Этот рассмотренный метод решения показательных уравнений относится к так называемому методу уравнивания показателей. Мы применили этот метод в рассмотрении и решении примеров 1 и 2.
Из других показательных уравнений нужно отметить такие, которые так же приводятся к уравниванию показателей и решение которых сводится к вынесению общего множителя за скобки.
Рассмотрим пример:
Решить уравнение: ![]()
Решение:
По свойству степеней имеем ![]()
![]()
Выносим за скобки общий множитель ![]() .
.
![]()
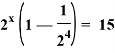
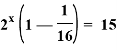
![]()
![]()
![]() = 16
= 16
![]() =
= ![]()
x = 4
Ответ: 4.
И, наконец, на решении двух примеров разного уровня сложности рассмотрим третий из основных методов — метод введения новой переменной.
Пример 1. Решить уравнение:
![]()
Решение:
Заметим, что ![]()
а ![]()
Перепишем заданное уравнение в виде:
![]()
Есть смысл ввести новую переменную y=![]() , тогда уравнение примет вид:
, тогда уравнение примет вид:
![]()
Решив квадратное уравнение относительноy, находим его корни:
![]() и
и ![]()
Но y=![]() ,значит остается решить два уравнения:
,значит остается решить два уравнения:
![]() = 4 и
= 4 и ![]() = -6
= -6
![]() нет корней, т. к. -6 < 0, а
нет корней, т. к. -6 < 0, а ![]() > 0 при
> 0 при
x = 2 любых значениях x.
Ответ: 2.
Пример 2. Решить уравнение:
![]()
Решение:
Воспользуемся тем, что:
− ![]() =
= ![]() ∙ 5
∙ 5
− ![]() =
= ![]()
− ![]() =
= 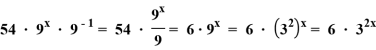
Получили:
![]() ∙ 5–13 ∙
∙ 5–13 ∙ ![]() +
+ ![]() = 0
= 0
Обе части уравнения разделим на ![]() ≠ 0, (уравнение однородное, второй степени), это позволит перейти к одному основанию.
≠ 0, (уравнение однородное, второй степени), это позволит перейти к одному основанию.
5 ∙ ![]() — 13 ∙
— 13 ∙ ![]() + 6 ∙
+ 6 ∙ ![]() =
= ![]()
5 ∙ ![]() - 13 ∙
- 13 ∙ ![]() + 6 = 0
+ 6 = 0
Теперь «появилась» новая переменная t = ![]() , относительно которой уравнение имеет вид квадратного уравнения:
, относительно которой уравнение имеет вид квадратного уравнения:
5![]() — 13t + 6t = 0
— 13t + 6t = 0
Корнями этого уравнения служат числа:
![]() =
= ![]() и
и![]() = 2
= 2
Решим два уравнения:
1) ![]() =
= ![]()
2) ![]() = 2
= 2
Решим два уравнения:
![]() =
= ![]()
x = -1
Решаем второе уравнение:
![]() = 2. Проблема?
= 2. Проблема?
Как представить число 2 в виде некоторой степени числа ![]() ?
?
Решение существует. Забегая вперед, скажем, что корень находится через логарифм. (Вернемся к этому позже).
Покажем единственный корень этого уравнения, применив графическую иллюстрацию. Построим в одной системе координат графики:
y = ![]() и y = 2
и y = 2
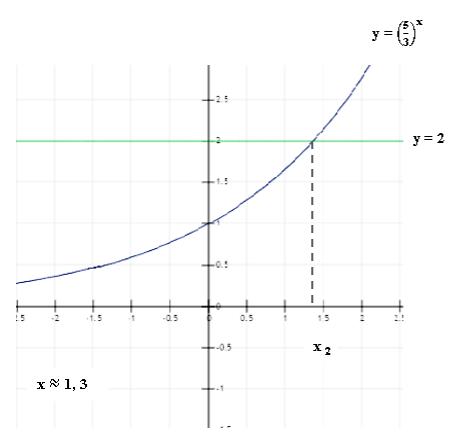
Ответ: ![]() = -1
= -1
![]() — корень уравнения
— корень уравнения ![]() = 2
= 2
Рассмотрим решение систем показательных уравнений
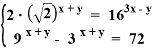
Для решения необходимо преобразовать уравнения системы к более простому виду.
Преобразуем 1 уравнение:
![]()
2∙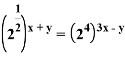
![]()
По свойству монотонности функции имеем:
1+![]()
![]()
2 + x + y = 24x— 8y
23x— 9y = 2
Преобразуем 2 уравнение системы к более простому виду:
![]()
Введем новую переменную, т. к. 9 = ![]() и
и ![]()
Пусть, 3x + y = t, тогда
![]()
D = ![]() - 4ac; D = 1 + 288 = 289
- 4ac; D = 1 + 288 = 289
![]()
![]()
Делаем обратную замену:
![]() = 9 и
= 9 и ![]() = -8— нет корней
= -8— нет корней
![]() =
= ![]()
x + y = 2— преобразованное второе уравнение.
Решим полученную систему:
![]()
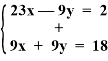
32x = 20
x = ![]()
x = ![]()
Из уравнения ![]() ,находим y
,находим y
![]() + y = 2
+ y = 2
y = 2— ![]()
y = 1![]()
Ответ: ![]() 1
1![]()
- Показательные неравенства.
Теперь переходим к рассмотрению решения показательных неравенств.
Дадим определение: показательными неравенствами называются неравенства вида ![]() , где a > 0, a ≠ 1, и неравенства, сводящиеся к этому виду.
, где a > 0, a ≠ 1, и неравенства, сводящиеся к этому виду.
Необходимо пользоваться следующей теоремой:
Показательное неравенство ![]() равносильно неравенству того же смысла f(x) > g(x), если a > 1 (т. е. знак не меняется, если функция y =
равносильно неравенству того же смысла f(x) > g(x), если a > 1 (т. е. знак не меняется, если функция y = ![]() — возрастающая. Примеры: y =
— возрастающая. Примеры: y = ![]() ; y =
; y = ![]() ; где 3 > 1 и 1,3 > 1).
; где 3 > 1 и 1,3 > 1).
Показательное неравенство ![]() равносильно неравенству противоположного смысла f(x) < g(x), если 0 < a < 1 (т. е. знак неравенства меняется, если функция y =
равносильно неравенству противоположного смысла f(x) < g(x), если 0 < a < 1 (т. е. знак неравенства меняется, если функция y = ![]() — убывающая. Примеры: y =
— убывающая. Примеры: y = ![]() или y =
или y = ![]() т. к. 0 < 0,5 < 1; и 0 <
т. к. 0 < 0,5 < 1; и 0 < ![]() < 1).
< 1).
Пример 1. Решить уравнения:
a) ![]()
![]()
Т. к. 2 > 1, то функция y = ![]() — возрастающая.
— возрастающая.
Получим:
2x— 4 > 6
2x > 10
x > 5
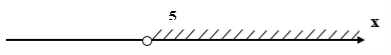
Ответ: (5; + ∞)
b) ![]()
т. к. ![]() =
= ![]() =
= ![]()
Перепишем
![]()
![]()
Т. к. 0 < ![]() < 1, то функция y =
< 1, то функция y = ![]() — убывающая.
— убывающая.
2x— 3,5 > ![]()
2x > 0,5 + 3,5
2x > 4
x > 2
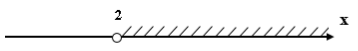
Ответ: (2; + ∞)
c) ![]()
т. к. 0 < 0,5 < 1, то функция y =![]() — убывающая.
— убывающая.
т. е. ![]()
![]()
![]()
Получили неравенство второй степени, которое решаем методом интервалов.
Рассмотрим функцию: f(x) = ![]()
Нули функции: f(x) = 0
![]() = 0
= 0
D = ![]() - 4ac; D = 36–32 =4
- 4ac; D = 36–32 =4
![]() =
= ![]() = 4
= 4
![]() =
= ![]() = 2
= 2

f(x) = (x— 2)∙(x— 4)
![]()
![]() Определим знаки в каждом из интервалов:
Определим знаки в каждом из интервалов:
![]()
![]() f(0) = (0–2)∙(0–4) > 0
f(0) = (0–2)∙(0–4) > 0
![]()
![]() f(3) = (3–2)∙(3–4) < 0
f(3) = (3–2)∙(3–4) < 0
f(5) = (5–2)∙(5–4) > 0
x € (-∞; 2] U [4; +∞)
Ответ: x € (-∞; 2] U [4; +∞)
Пример 2. Рассмотрим решение более сложного неравенства:
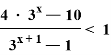
По свойству ![]() =
= ![]() ∙ 3; введем новую переменную y =
∙ 3; введем новую переменную y = ![]()
Получим
![]()
![]()
![]()
![]()
![]()
Решаем методом интервалов:
Рассмотрим функцию f(x) = ![]()
Нули функции: f(x) = 0; ![]() = 0 → y— 9 = 0, т. о. y = 9
= 0 → y— 9 = 0, т. о. y = 9
Нули знаменателя
![]() = 0
= 0
3y = 1
y = ![]()
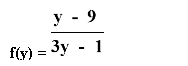 Применяем метод интервалов.
Применяем метод интервалов.
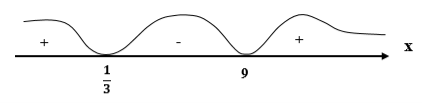
f(0) = ![]() > 0
> 0
f(1) = ![]() < 0
< 0
f(10) = ![]() > 0
> 0
Находим ![]() < y < 9
< y < 9
Возвращаемся к переменной x, получим двойное неравенство
![]() <
< ![]() < 9
< 9
![]() <
< ![]() <
< ![]()
т. к. 3 > 1, то функция y = ![]() — возрастающая.
— возрастающая.
—1 < x < 2
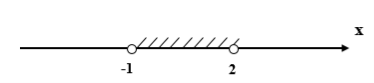
Ответ: (-1;2)
Для более полного объема информации решения неравенств, необходимо рассмотреть трансцендентные неравенства, в которых левая и правая части не приводятся к одному основанию. Их можно решить лишь графическим способом, используя иллюстрацию.
Например, решить неравентва:
a) ![]() ;
;
b) ![]()
Решение:
Построим в одной системе координат графики функций y = ![]() и y =
и y = ![]()
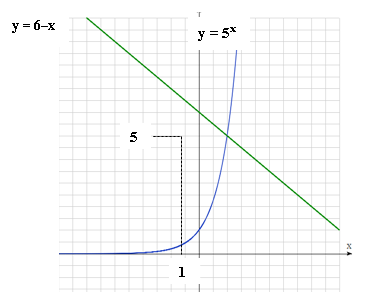
y = ![]()
|
x |
-1 |
0 |
1 |
|
y |
1/5 |
1 |
5 |
y = ![]()
|
x |
0 |
3 |
|
y |
6 |
3 |
Графики пересеклись в одной точке (1; 5)
Абсцисса точки пересечения является единственным корнем уравнения ![]()
Нас интересует решение неравенства ![]()
По иллюстрации график показательной функции y = ![]() лежит выше прямой y =
лежит выше прямой y = ![]() , если
, если ![]() > 1 (хорошо видно из рисунка).
> 1 (хорошо видно из рисунка).
Значит, решение неравенства ![]() можно записать так: x ≥ 1
можно записать так: x ≥ 1
Ответ: [1;+∞)
б)![]()
График y = ![]() ниже y =
ниже y = ![]() при x < 1
при x < 1
Ответ: (-∞; 1)
Итак, обобщим полученный опыт в решении уравнений и неравенств через алгоритмы.
- Общий вид стандартного показательного уравнения:
![]()
![]()
- Приведение к одному основанию:
1) ![]()
2) ![]()
3) x = c
- Графический:
![]()
1) 
2) Найти абсциссы (x) точек пересечения.
3) Ответ.
- Вынесение за скобку степени с наименьшим показателем:
1) Вынести степень за скобку (![]() ;
;
2) Вычислить числовое значение в скобках (?);
3) Разделить обе части на (?);
4) Прийти ![]() ;
;
5) Решить ![]() (см. выше);
(см. выше);
6) Получить ответ.
- Приведение к квадратному уравнению:
1) Записать в виде:
A![]() + B
+ B![]() + C = 0
+ C = 0
2) Обозначить ![]() = t
= t
3) Решить квадратное уравнение A![]() + Bt + C = 0
+ Bt + C = 0
4) ![]()
![]()
5) Решить стандартные уравнения
6) Ответ.
Для закрепления, анализа и самопроверки предлагаются следующие задания (алгоритм решения смотри выше).
Задания предлагаются для двух вариантов
- Какие из перечисленных ниже неравенств будут верными, если:
I ВариантII Вариант
a > 1 0 < a < 1
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
- Решить уравнения:
I Вариант
1) ![]()
2) ![]()
3) ![]()
4) 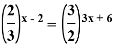
II Вариант
1) ![]()
2) ![]()
3) ![]()
4) 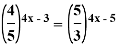
- Решить уравнения
I Вариант
1) ![]()
2) ![]()
II Вариант
1) ![]()
2) ![]()
- Задания с применением классификации.
Выписать уравнения, решаемые способом приведения к общему основанию, и решить их.
I вариант
1) ![]()
2) ![]()
3) ![]()
4) ![]()
(задание повышенной сложности).
II вариант
1) ![]()
2) ![]()
3) ![]()
4) ![]()
(задание повышенной сложности)
- Выписать уравнения, решаемые только графическим способом и решить их.
I вариант
1) ![]()
2) ![]()
3) ![]()
II вариант
1) ![]()
2) ![]()
3) ![]()
Решить остальные уравнения.
- Решить неравенства:
I вариант
1) ![]()
2) ![]()
3) ![]()
4) ![]()
II вариант
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Литература:
- Учебник: «Алгебра и начала анализа 10–11» / А. Г. Мордкович.
- Учебник: «Алгебра и начала анализа 10–11» / А. Н. Колмогоров.
- «Сборник заданий для проведения письменного экзамена 11 кл.» / Г. В. Дорофеев.
- «Тренировочные задания ЕГЭ» / ЭКСМО / Т. А. Корешкова.
- «Экзаменационные материалы для подготовки к ЕГЭ 2006» / Коммерсант / А. Г. Клово.
- Методические рекомендации по изучению тем «Показательная, логарифмическая, степенная функции» / Н. К. Беденко.

