В данной статье рассматривается кластер автоколебательных систем на основе двух связанных нейронов ФитцХью — Нагумо. Исследования показали, что в данном кластере есть 4 режима генераций сигналов. Однако в данной работе определено что, переход от одного режима к другому происходит не только по заданным параметрам, но и из-за влияния шумов и флуктуаций.

In this paper we consider a cluster of self-oscillating systems based on two coupled FitzHugh — Nagumo neurons. Studies have shown that in this cluster there are 4 modes of signal generation. However, in this paper it is determined that the transition from one regime to another occurs not only from given parameters, but also because of the influence of noise and fluctuations.

В качестве автоколебательной системы рассмотрена модель нейрона ФитцХью —Нагумо [1], а кластер образовывается отрицательно связью между нейронами.

(1)

В результате теоретических, численных и экспериментальных исследований динамики рассматриваемой автоколебательной системы, определены 4 режима генерации сигналов: «быстрый», «медленный», «bursting», «покой». Так же в этой система на границе потери устойчивости определена «двухчастотная» бифуркация Хопфа. В связи с этим для определения «двухчастотной» бифуркаций Хопфа [2] должно выполнится следующее условие:

(2)

На рисунке 1 показано, как в пространстве переменных a1 и a2 отображено условие возникновения бифуркаций Хопфа. На этом график уравнению 2 соответствует дуга круга выделенная жирной линией.

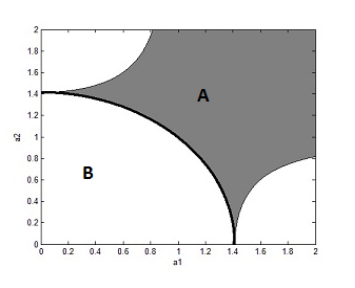
Рис. 1. Условие возникновения бифуркаций Хопфа , и

На рисунке 1 показаны условия, при которых возникают режимы «bursting» сектор B и режим «покоя» сектор A. Условия для возникновения этих режимов выглядит следующим образом:

, (3)

При численном исследований кластера автоколебательных систем с заданными дифференциальными уравнениями все режимы сигналов соответствовали графику представленным на рисунке 1. При этом точность интегрирования была взята σ = . При эксериментальном моделирований системы, сигналы генерируемые кластером не соответсвовали тем областям в пространстве переменных a1 и a2.

1. Эксперимент

Как известно кластер автоколебательных систем генерирует 4 режима сигналов. При численных исследованиях все режимы соответствуют условиям возникновения их по заданным параметрам (рисунок 2).

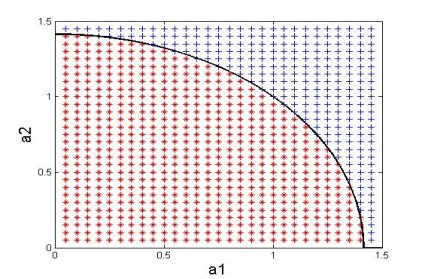
Рис. 2. Численное исследование режимов генераций сигналов (*-«bursting», +-«покой»)

На рисунке 3 показан график режима «покоя» при численом иследований.

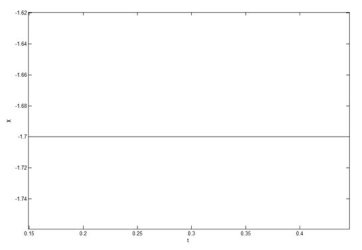
Рис. 3. Режим «покоя» численное исследование

При экспериментальном исследований в данном режиме при определенных значениях намного превышающих условие (3) были определены режим «покоя» с наличием шумов и флуктуаций.

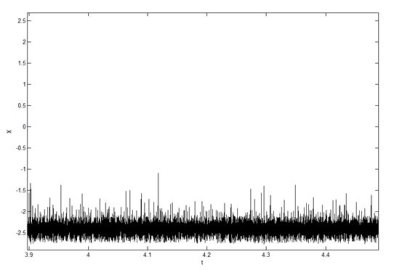
Рис. 4. Режим «покоя» экпериментальное исследование

Используя данные результаты было проведено численное исследование при точности интегрирования σ = , что соотвествует реальному шуму в эксперименте. Определено что границы равновесия устойчивости системы меняются под влиянием шумов и флуктуаций.

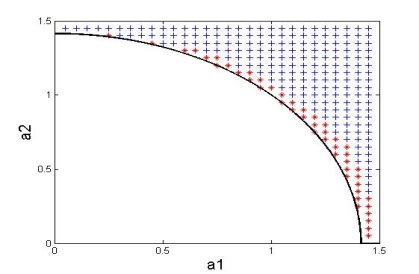
Рис. 5. Условия возникновения сигналов при σ = .

2. Заключение

В результате данных исследований определено, что качественный переход между режимами происходит из-за шумов и флуктуаций. Однако, стотит отметить что, переход от режима в другой из шумов происходит около границы устойчивости системы.

Литература:

1. Jane Cronin. Mathematical aspects of Hodgkin-Huxley neural theory. Cambridge University Press. 1987.
2. B. Medetov, G. Weiss, Zh. Zhanabaev, M. Zaks. Numerically induced bursting in a set of coupled neuronal oscillators. //Communications in Nonlinear Science and Numerical Simulation. 2014.
3. А.С. Койшигарин, Б.Ж. Медетов, Н. Албанбай. Численное исследование влияния шума и флуктуаций на режимы генерации кластером автоколебательных систем. Теория. — Алматы: Журнал проблем эволюции открытых систем, 2015 г., вып. 17, том 1.
4. Б.Ж. Медетов, Н. Албанбай, А.С. Койшигарин, К.А. Ниязалиев. ФитцХью-Нагумо нейрондарынан құралған кластердің шуыл әсерінен «тыныштық» күйден «bursting» режиміне көшуін эксперименталдық зерттеу. — Алматы: Сборник тезисов. Международная конференция молодых ученых «ФАРАБИ ӘЛЕМІ», 13-16 апреля, 2015 г., стр. 421.