Преобразование Фурье как основополагающий частотный метод улучшения изображений

Повышение качества изображения остается открытой проблемой современных технологий. В данной работе рассмотрены частотные методы улучшения изображений, а в частности использование Фурье преобразования с различными способами фильтрации для повышения качества картинки.

Ключевые слова: частотная фильтрация, преобразование Фурье, улучшение изображений

Преобразование Фурье (ПФ) является одним из самых действенных частотных методов в области улучшения изображений, однако практическая реализация данного инструмента обработки до сих пор обладает значительной сложностью восприятия. В этой работе мы опишем основные принципы Фурье анализа, а также особенности его применения в качестве частотного метода обработки изображений.

Благодаря работе французского математика Жана Батиста Жозефа Фурье изданной в 1822 году в книге «Аналитическая теория тепла» нам стало известно о том, что любая функция, периодически воспроизводящая свои значения, может быть представлена в виде суммы косинусов (синусов) различных частот, умноженных на некоторые коэффициенты. Позже это сумма стала называться рядом Фурье. Являющееся сейчас чем-то очевидным и общепризнанным, в свое время данное утверждение подверглось большой критике и было признанно только более чем через пол века. В Случае, когда представляемая функция не является периодической, она может быть выражена в виде интеграла от произведения синусов (косинусов) на некоторую постоянную функцию. Данный интеграл и называется преобразованием Фурье. Одной из важнейших особенностей этих представлений является то, что они могут быть полностью восстановлены, совершенно без потери информации при помощи определенной процедуры обращения. Данная особенность делает их широко используемыми фундаментальными инструментами в область фурье-анализа, и предоставляет методы решения для большого спектра задач [1].

Преобразование Фурье используется во многих областях науки — в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть обратимый переход от временного пространства (time domain) в частотное пространство (frequency domain). Богатые возможности применения основываются на нескольких полезных свойствах преобразования [1].

Прямое преобразование Фурье представляется собой образ непрерывной функции одной переменной и определяется как:

где (мнимая единица). Для данного образа можно легко получить исходную функцию, воспользовавшись формулой для обратного преобразования Фурье [2]:

Рассмотренные функции являются обратными, а вместе составляют фурье-пару. Преобразования для функции двух переменных происходит аналогичным образом.

Дискретное преобразование Фурье — преобразование конечных последовательностей (комплексных) чисел, которое, как и в непрерывном случае, превращает свёртку в поточечное умножение. Используется в цифровой обработке сигналов и в других ситуациях, где необходимо быстро выполнять свёртку, например, при умножении больших чисел. Дискретное преобразования Фурье (ДПФ) на конечной области для функции одной переменной , где определяется как [1]:

,

Данное преобразование является основным в частотной области улучшения изображений. Для прямого дискретного преобразования Фурье так же можно построить обратное. В отличие от преобразований, построенных на бесконечной области, в которых необходимо проводить вычисления, определяющие существование ДПФ и обратного, здесь эта необходимость отпадает. Оно всегда существует.

Теперь нам необходимо понять, что же представляет собой частотная область. Ее определение прямо следует из формулы Эйлера:

Если поставить данное выражение в формулу для ДПФ и использовать нечетность синуса и четность косинуса получим:

,

Таким образом можно заметить, что значение для каждого значения состоит из суммы всех значений функции , которые в свою очередь умножаются на синусы и косинусы разных частот. Частотной областью называется область значений переменной , на которой принимает свои значения функция , поскольку частоты слагаемых, составляющих преобразование, определяются значением переменной . Простыми словами, преобразование Фурье можно сравнить со своего рода математической призмой (по аналогии со стеклянной призмой, которая разлагает свет в зависимости от длины волны (т. е. частоты)). Оно позволяет нам описать функцию, как совокупность составляющих ее частот. Это и является основной задумкой, которая лежит в основе методов линейной фильтрации.

За счет описанного выше свойства, зачастую невозможно установить соответствие между образом и изображением. Однако, интуитивно понятно, что частоты в преобразовании связаны с вариациями яркости на изображении. Например, на картинке более низким значениям частот, обозначенных в начале оси координат Фурье, преобразования будут отвечать плавные изменения яркости в пределах одного однотонного объекта, тогда как по мере удаления от начала координат будут появляться высокие частоты, которые будут соответствовать более быстрому изменению яркости, например, на границах двух разных объектов.

1. Перед вычислением преобразования Фурье умножить исходное изображение на 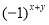, с целью его центрирования и подтверждения что ПФ существует.
2. Вычислить прямое ДПФ 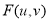для полученного изображения.
3. Умножить 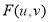на функцию фильтра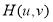
4. Вычислить обратное ДПФ от значения, полученного на шаге 3.
5. Выделить вещественную часть результата.
6. Умножить на 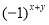для получения финального значения.

Только что описанная процедура фильтрации изображена на рис 1.

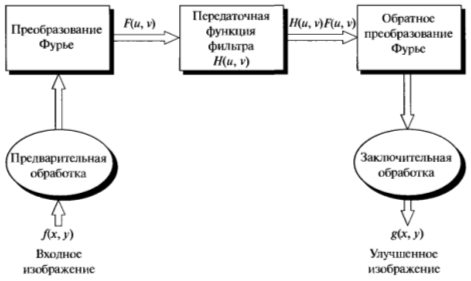
Рис. 1. Основные этапы фильтрации в частотной области

Значение множителя может быть различным, в зависимости от необходимых нам свойств. Низкие частоты Фурье преобразования отвечают за возникновение преобладающих значений яркости на гладких участках сети, в то время как высокие частоты ответственны за такие детали, как контуры и шум. Таким образом, возникает возможность создания высокочастотных и низкочастотных фильтров. Высокочастотные фильтры ослабляют значения низких частот, пропуская только высокие. Низкочастотный действует в точности наоборот. После его применения изображение будет содержать меньше резких деталей, поскольку большие значения яркости подавлены.

Несмотря на то, что преобразование Фурье является наилучшим инструментом частотной фильтрации, можно достигнуть еще большей эффективности его использования в совокупности с методами пространственной фильтрации. Наиболее важная взаимосвязь областей пространственной и частотной фильтрации достигается при помощи свертки, процедуры, в основе которой лежит просмотр каждой области изображения при помощи маски фильтра для поиска определенной величины. Формально дискретная свертка двух функций и определяется как [4]:

где размеры свертки. В отличие от частотной фильтрации, в пространственной используются фильтры гораздо меньшего размера. С другой стороны фильтрация в частотной области почти всегда оказывается наглядной. Таким образом, мы можем задать фильтр в частотной области, вычислить его прообраз, а затем использовать полученный пространственный фильтр, как ориентир для построения маски меньшего размера.

Фурье преобразования являются частным случаем гауссовых функций. На их основе могут быть построены и более сложные фильтры, например высокочастотный фильтр состоящий из двух гауссовых функций.

Анализ в частотной области позволяет выявить значительное число методов того, как выбрать фильтр для улучшения изображения. Таким образом, наш подход состоит в отыскании небольшой пространственной маски, которая бы отражала сущность метода фильтрации [4,5]

К достоинствам методов линейной фильтрации, в том числе преобразования Фурье, следует отнести их ясный физический смысл и простоту анализа результатов. Однако при резком ухудшении соотношения сигнал/шум, при возможных вариантах площади зашумления и наличии высокоамплитудного импульсного шума линейные методы предварительной обработки могут оказаться недостаточными. В этой ситуации значительную помощь оказывают нелинейные методы, оставляя в качестве основы именно частотную фильтрацию.

1. Гонсалес Р., Вудс Р. Цифровая обработка изображений //М.: Техносфера. — 2012. — Т. 1104.
2. Залогова Л. Компьютерная графика. — М.: Лаборатория Базовых Знаний, 2005.
3. Лукин А. Введение в цифровую обработку сигналов //М.: МГУ. Лаборатория компьютерной графики и мультимедиа. — 2002.
4. Айфичер Э. С. Цифровая обработка сигналов: практ. подход: [пер. с англ.]. — Издательский дом Вильямс, 2008.
5. Чутченко Ю. Е., Преображенский А. П. Исследование возможности улучшения качества изображения //Территория науки. — 2007. — №. 3.