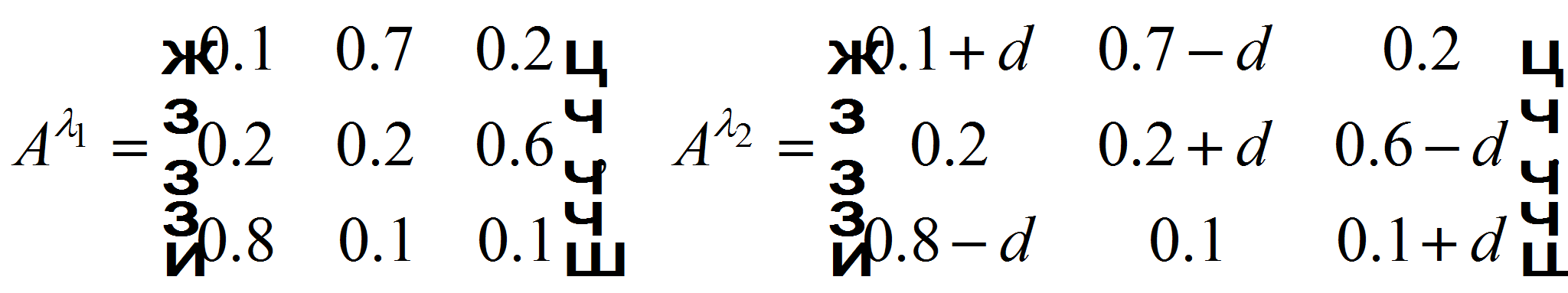- По своей природе скрытые марковские модели (СММ) позволяют непосредственно учитывать пространственно-временные характеристики последовательностей и поэтому получили широкое применение [1], [2]. Имея хорошие описательные способности, СММ не всегда демонстрируют необходимые дискриминирующие свойства, важные для задач классификации.
- Задачу классификации будем понимать в следующем смысле. Имеется исходное множество объектов, разделённых экспертом на классы (обучение с учителем). Из него каким-либо способом отбирается часть объектов, образующих обучающую выборку. Требуется построить алгоритм, способный классифицировать произвольный тестовый объект из исходного множества.
-
СММ полностью описывается ненаблюдаемой
(скрытой) марковской цепью, вероятностями наблюдаемых символов и
вероятностями начальных состояний:
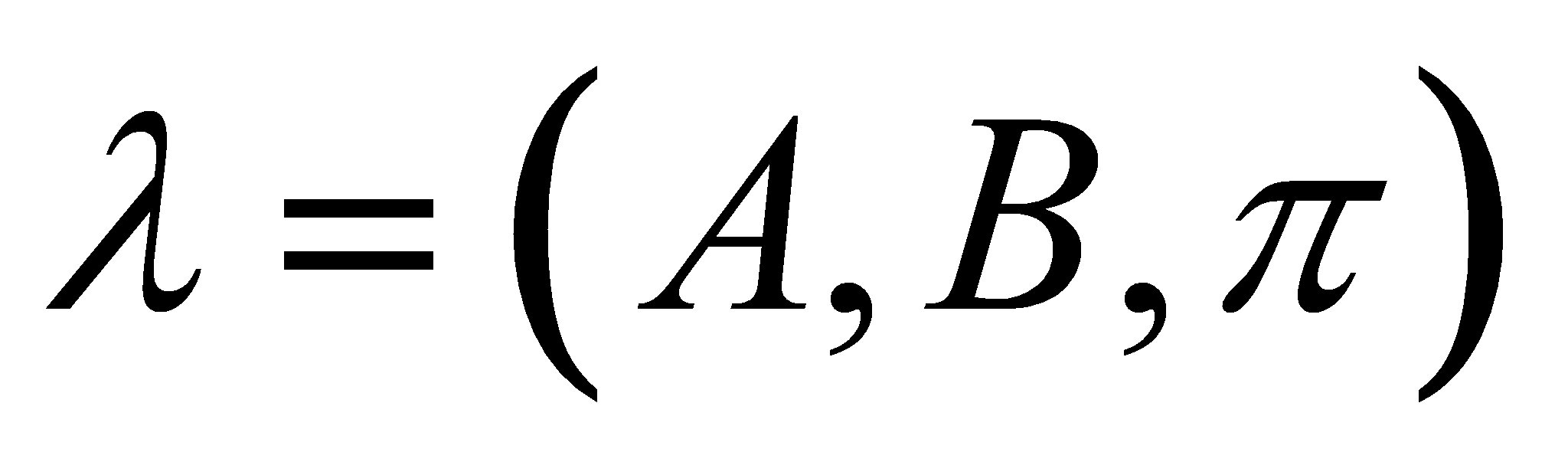 .
В данной работе рассматривается случай, когда функция распределения
вероятностей наблюдаемых символов описывается смесью нормальных
распределений. Параметры смеси задаются таким образом, чтобы скрытое
состояние ассоциировалось лишь с одним своим наблюдаемым состоянием.
.
В данной работе рассматривается случай, когда функция распределения
вероятностей наблюдаемых символов описывается смесью нормальных
распределений. Параметры смеси задаются таким образом, чтобы скрытое
состояние ассоциировалось лишь с одним своим наблюдаемым состоянием. -
Традиционно при использовании СММ
используется классификатор, основанный на отношении логарифмов
функций правдоподобия: последовательность
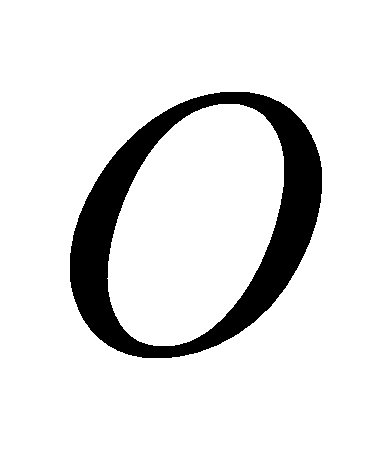 считается порожденным моделью
считается порожденным моделью
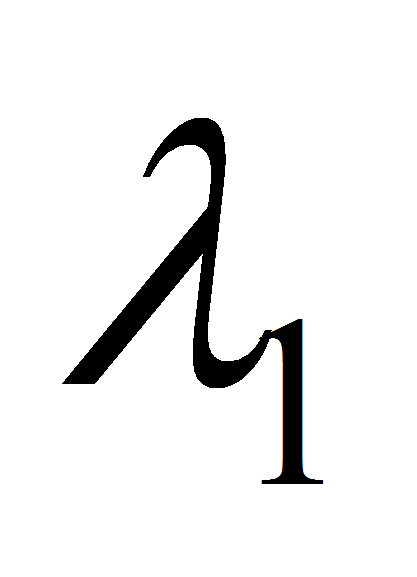 ,
если выполняется:
,
если выполняется:
|
(1) |
MERGEFORMATИначе – считается, что
последовательность порождена моделью
![]() .
При неизвестных параметрах моделей
.
При неизвестных параметрах моделей
![]() и
и
![]() сначала производится их оценка (например, с использованием метода
максимального правдоподобия [1]).
сначала производится их оценка (например, с использованием метода
максимального правдоподобия [1]).
- Если конкурирующие модели близки по параметрам, а наблюдаемые последовательности не являются чисто гауссовскими последовательностями, то традиционная техника классификации с применением (1) далеко не всегда дает приемлемые результаты.
-
Для приближения к реальной ситуации все
наблюдаемые последовательности при моделировании подвергались
искажению. Задача состояла в сравнении в этих условиях возможностей
традиционной методики классификации, основывающейся на (1), с
классификатором k
ближайших соседей (kNN)
в пространстве признаков, в качестве которых использовались первые
производные от логарифма функции правдоподобия по элементам матрицы
 двух моделей
двух моделей
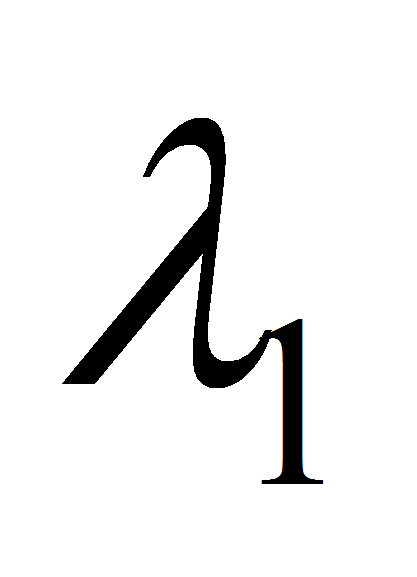 и
и
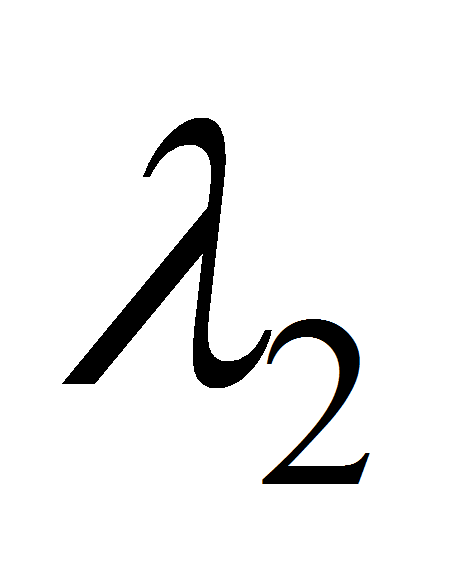 [3].
Предложенная схема классификации описана в [4].
[3].
Предложенная схема классификации описана в [4]. - Зашумление производилось по двум различным схемам:
|
(2) | |
|
(3) |
- Схема (2) использовалась для моделирования аддитивного шума, а (3) – для вероятностного шума. Оба случая также подразделялись на схему с шумом, имеющим одинаковые параметры в каждом скрытом состоянии модели, и схему с разными параметрами.
- Исследования проводились при следующих условиях. Две модели определены на одинаковых по структуре скрытых марковских цепях и различаются только матрицами переходных вероятностей:
- Параметры гауссовских распределений
для моделей
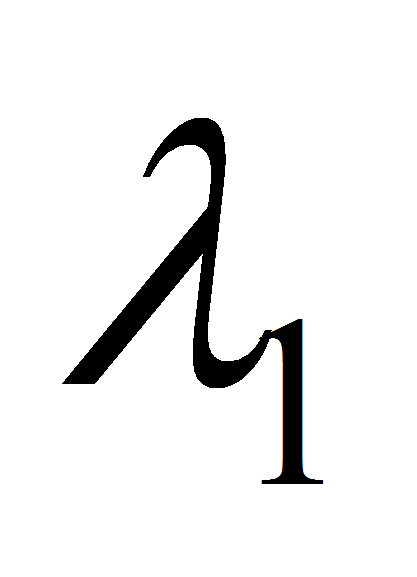 и
и
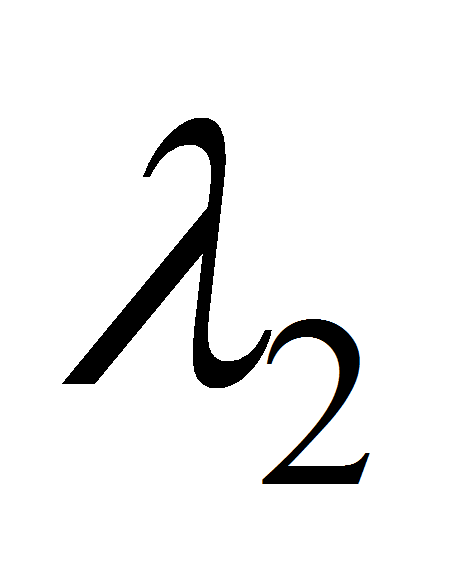 выбирались одинаковыми:
выбирались одинаковыми:
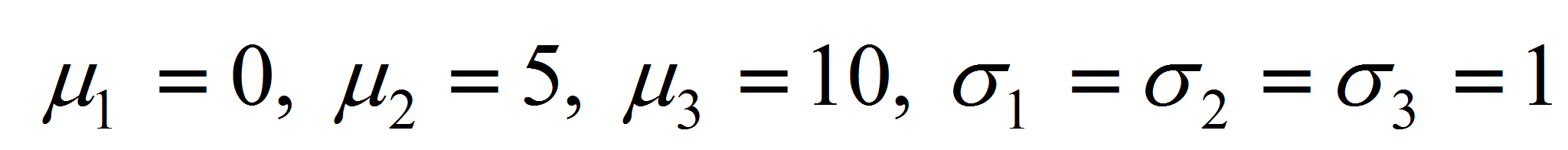 .
Вероятности начальных состояний также совпадали:
.
Вероятности начальных состояний также совпадали:
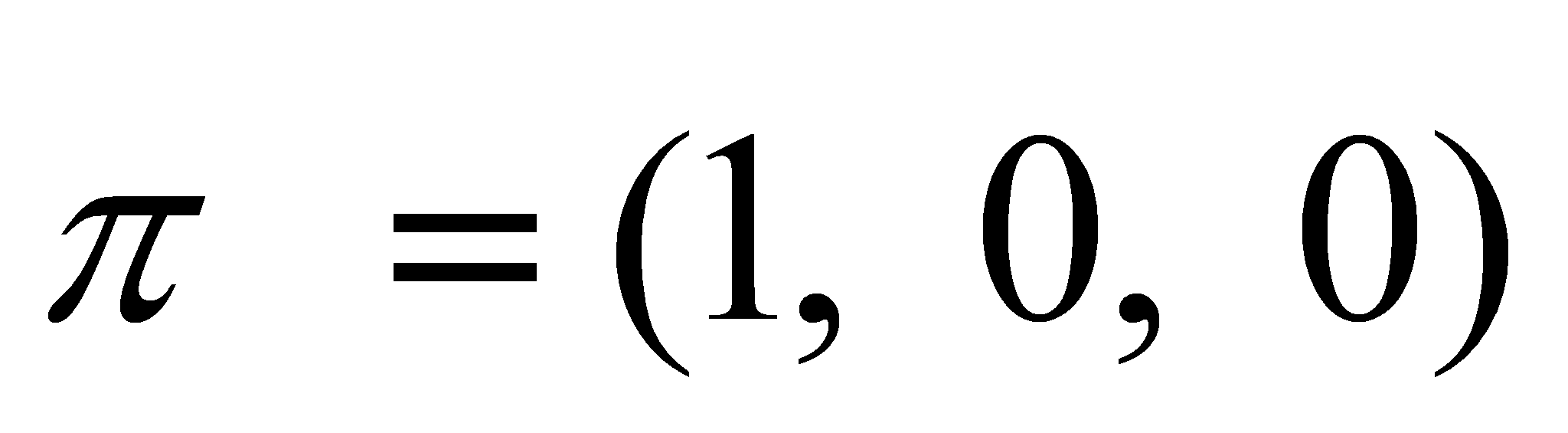 .
. -
Обучающие и тестовые последовательности
моделировались по методу Монте-Карло. Для проведения экспериментов
было сгенерировано по 5 обучающих наборов последовательностей. К
каждому набору этих последовательностей моделировалось по 5 тестовых
наборов. Каждый набор содержал по 100 последовательностей для
каждого класса. Таким образом, всего было смоделировано
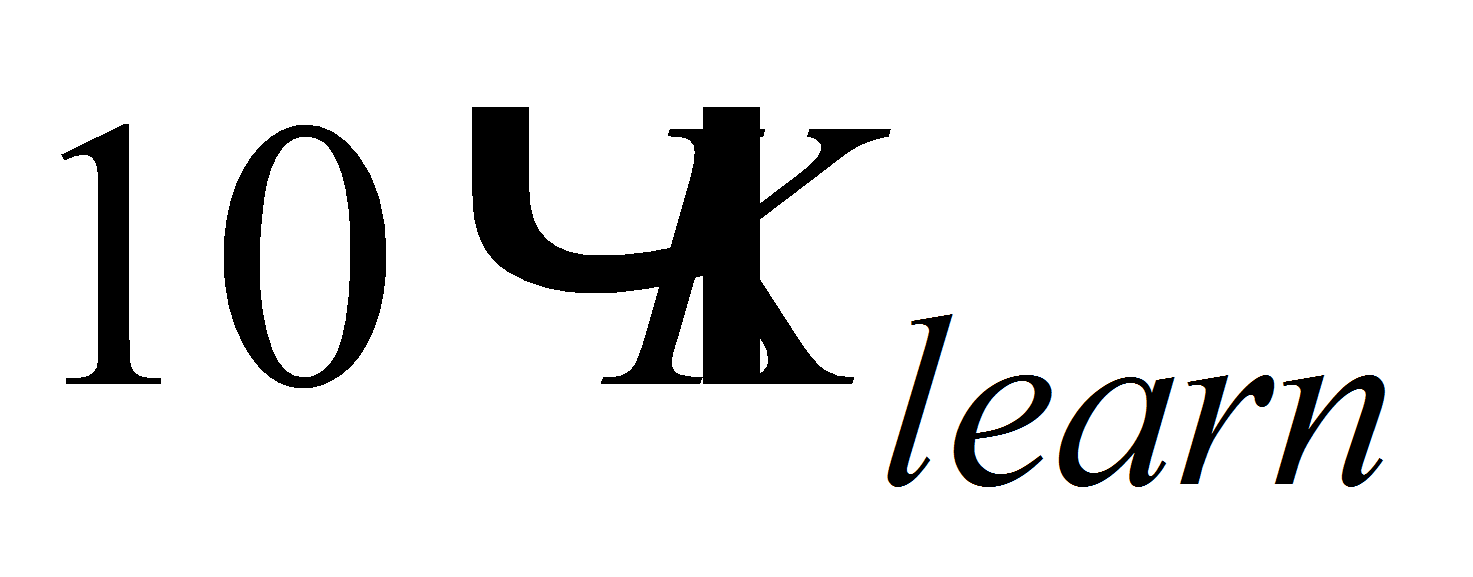 обучающих и 1000 тестовых последовательностей. Здесь
обучающих и 1000 тестовых последовательностей. Здесь
 – это количество обучающих последовательностей в каждом
классе. Результаты классификации усреднялись.
– это количество обучающих последовательностей в каждом
классе. Результаты классификации усреднялись. -
Исследования проводились при разном уровне
шума
 и
и
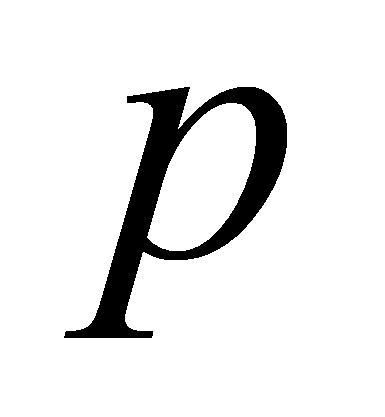 ,
различной длине последовательностей
,
различной длине последовательностей
 ,
степени близостей моделей по матрице
,
степени близостей моделей по матрице
 ,
количестве обучающих последовательностей
,
количестве обучающих последовательностей
 .
В качестве распределения шума было выбрано распределение Коши, т.к.
это распределение имеет тяжелые хвосты и часто используется как
некий индикатор в исследованиях, связанных с робастными методами
оценивания параметров. Это было сделано для того, чтобы посмотреть,
как ведет себя традиционный классификатор в сравнении с
классификатором, базирующимся на kNN.
.
В качестве распределения шума было выбрано распределение Коши, т.к.
это распределение имеет тяжелые хвосты и часто используется как
некий индикатор в исследованиях, связанных с робастными методами
оценивания параметров. Это было сделано для того, чтобы посмотреть,
как ведет себя традиционный классификатор в сравнении с
классификатором, базирующимся на kNN. - Ниже приводится сравнение качества классификации зашумленных последовательностей при используемых схемах (2) и (3) для шума с одинаковыми параметрами в каждом скрытом состоянии и с разными параметрами в скрытых состояниях.
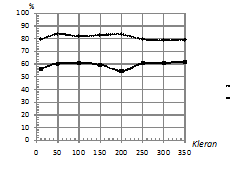
- Далее на всех рисунках график, отражающий результаты классификации для kNN, имеет пунктирную линию, а график для традиционного подхода – сплошную линию.
-
На рис. 1 (а) – рис. 8 (а) приведены
зависимости процента верно классифицированных последовательностей
при распределении ошибок по закону Коши с параметрами, одинаковыми
для каждого скрытого состояния:
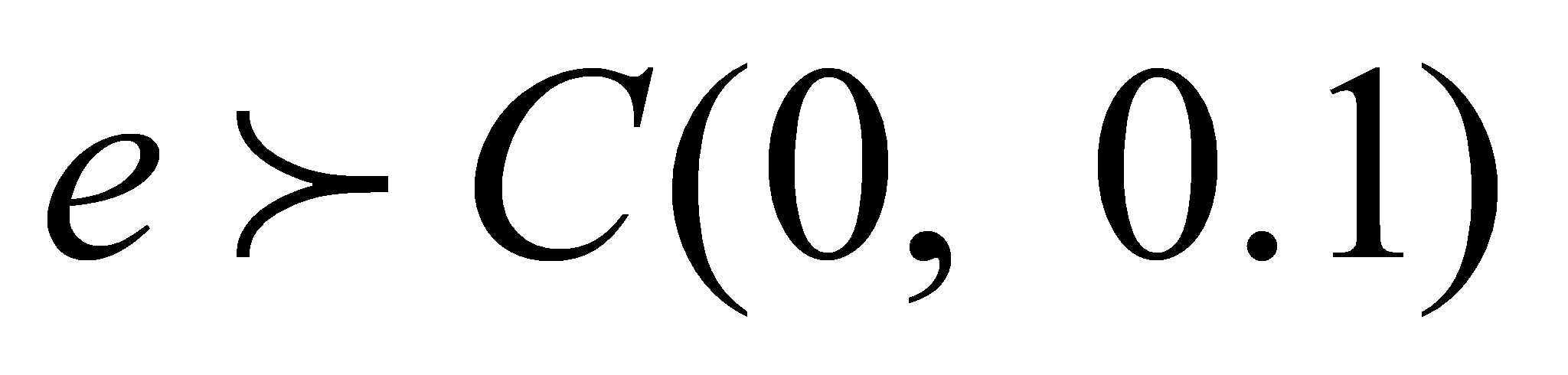 ,
и на рис. 1 (б) – рис. 8 (б) – по закону Коши с
параметрами разными для каждого скрытого состояния:
,
и на рис. 1 (б) – рис. 8 (б) – по закону Коши с
параметрами разными для каждого скрытого состояния:
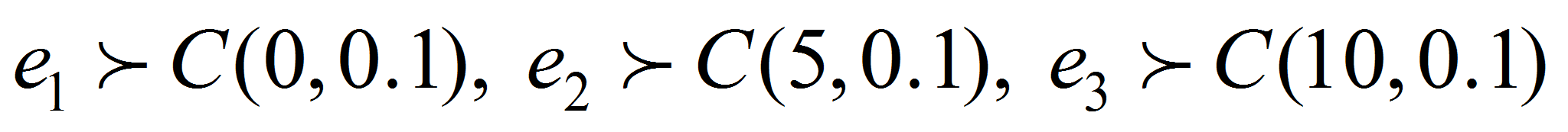 .
.
- На рис. 1 – 4 приведены
зависимости для аддитивного шума. При этом параметры (если в
зависимости от них не изменялись проценты классификации на
графиках), заданы следующим образом:
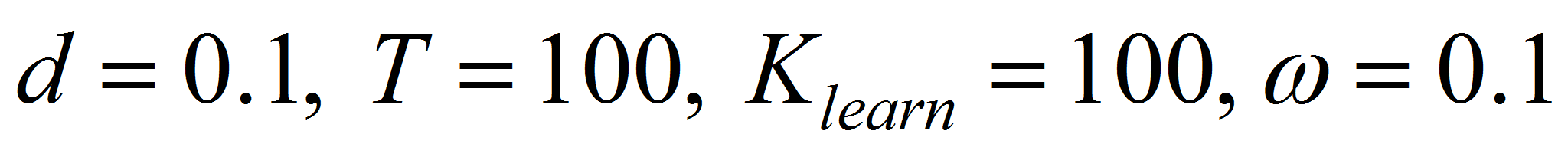 .
. -
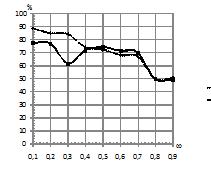
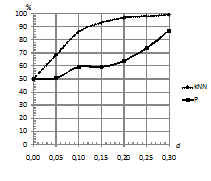
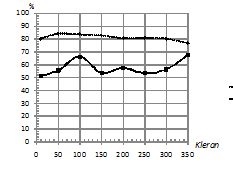
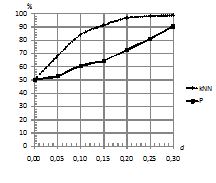
По рис. 1 видно, что при шуме, одинаковом
в каждом скрытом состоянии (рис 1 (а)), идет снижение качества
классификации, в то время как при шуме, разном в каждом скрытом
состоянии, наблюдается постепенное увеличение процента верно
классифицированных последовательностей (рис. 1 (б)). Это объясняется
тем, что во втором случае шум воспринимается не как искажение, а как
наблюдаемый сигнал, т.к. параметры смещения шума и нормальных
распределений для СММ
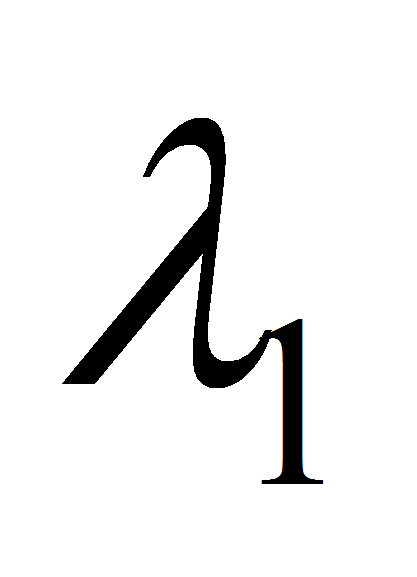 и
и
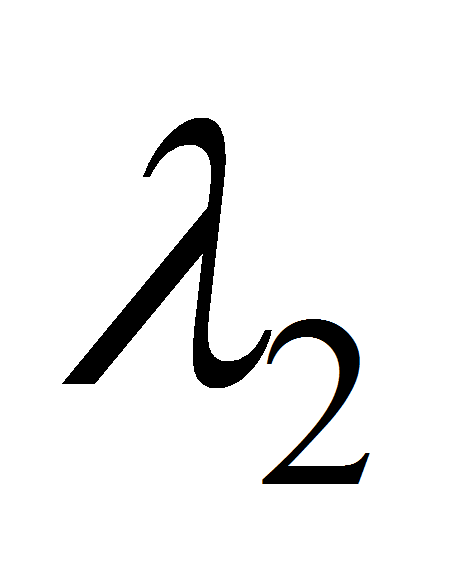 совпадают.
совпадают.
|
а) |
б) |
|
Рис. 1. Зависимость
процента верно классифицированных последовательностей от уровня
шума
| |
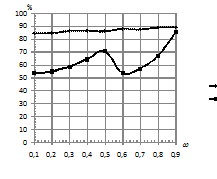
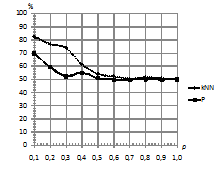
На рис. 2 наблюдается одинаковый
характер зависимостей: чем модели дальше по параметру
![]() ,
тем выше процент верной классификации как для стандартной методики,
так и для kNN.
,
тем выше процент верной классификации как для стандартной методики,
так и для kNN.
|
а) |
б) |
|
Рис. 2. Зависимость
процента верно классифицированных последовательностей от параметра
близости моделей
| |
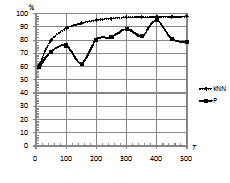
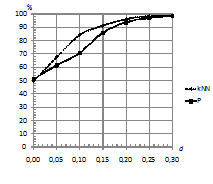
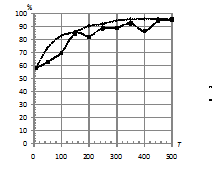
На рис. 3 (б) наблюдается интересный эффект: с увеличением длины последовательностей процент верно классифицированных последовательностей остается на одном и том же уровне (около 60%).
|
а) |
б) |
|
Рис. 3. Зависимость
процента верно классифицированных последовательностей от длины
последовательности
| |
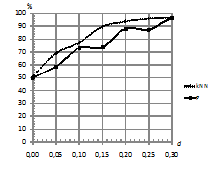
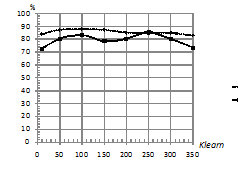
На рис. 4 наблюдается то, что увеличение
числа обучающих последовательностей не влечет увеличения качества
классификации, причем для kNN
наблюдается эффект переобучения: снижение
процента верной классификации при росте
![]() .
.
|
а) |
б) |
|
Рис. 4. Зависимость
процента верно классифицированных последовательностей от
количества обучающих последовательностей в каждом классе
| |
- На рис. 5 – 8 приведены
зависимости для вероятностного шума. При этом параметры (если в
зависимости от них не изменялись проценты классификации на графиках)
заданы следующим образом:
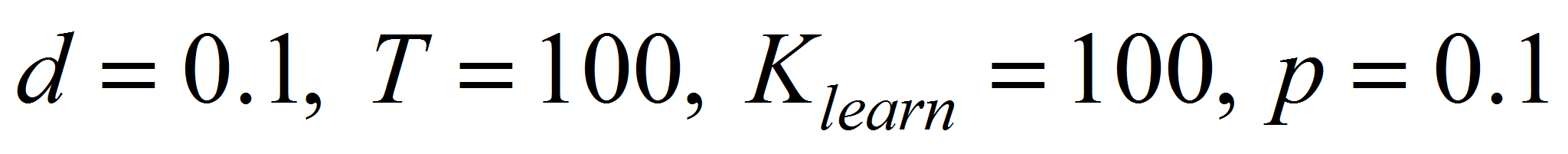 .
. -
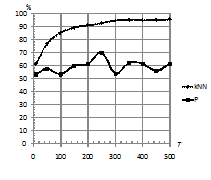
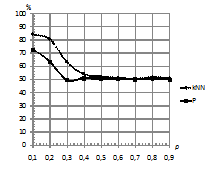
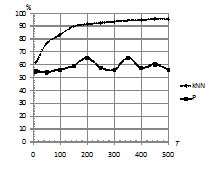
На рис. 5 наблюдается постоянное снижение
процента верной классификации (при
 ).
).
|
а) |
б) |
|
Рис. 5. Зависимость
процента верно классифицированных последовательностей от
вероятности возникновения шума
| |
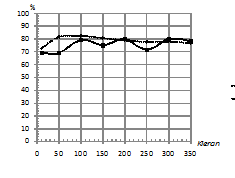
Характер зависимостей, приведенных на рис. 6 – рис. 8 аналогичен зависимостям на рис. 2 – рис. 4.
- Судя по проведенным исследованиям, можно сделать вывод, что предложенный классификатор, базирующийся на метрическом алгоритме классификации kNN, имеет процент верно классифицированных зашумленных последовательностей выше, чем классический классификатор, основывающийся на отношении логарифмов функций правдоподобия. Следует также отметить более пологое изменение графика, отображающего процент верной классификации для kNN, в сравнении с графиком для традиционной методики. Это объясняется тем, что используемый шум, распределенный по закону Коши, относится к распределениям с тяжелыми хвостами, и в этих условиях оценки параметров базового нормального распределения, полученные по методу максимального правдоподобия, становятся смещенными.
- Используя модель шума, имеющего разные параметры в каждом скрытом состоянии, в целом получаются результаты, сходные с результатами классификации при шуме с одинаковыми параметрами. Однако классификатор, основанный на kNN, в данном случае выигрывает в сравнении с традиционной методикой классификации в среднем на 20 %, что является весьма существенным аргументом для применения предложенного метода при классификации реальных зашумленных сигналов.
-
- Литература:
- Rabiner, L.R. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition / L.R. Rabiner // Proceedings of the IEEE. – 1989. – 77 (2). – P. 257-285.
- Cappe, O. Ten years of HMM [Электронный ресурс] / O. Cappe; CNRS, LTCI & ENST, Dpt. TSI. – Режим доступа: http://perso.telecom-paristech.fr/~cappe/docs/hmmbib.html.
- Гультяева, Т.А. Особенности вычисление первых производных от логарифма функции правдоподобия для скрытых марковских моделей при длинных сигналах / Т.А. Гультяева // Сборник Научных трудов НГТУ.. – Новосибирск : Изд-во НГТУ, 2010. – № 2(60). – С. 47-52.
- Гультяева Т. А. Повышение классификационных свойств скрытых марсковских моделей / Т. А. Гультяева // Информатика и проблема телекоммуникаций: Материалы российской науч.-технич. конф. - Новосибирск: Изд-во СибГУТИ, 2010. - Том I. - C. 52-54.