Выбор одного из методов построения модели системы зависит от априорной информации о ней. Если субъект обладает ограниченной информацией, например, только выборкой наблюдений входных и выходных воздействий системы, то моделирование можно произвести одним из непараметрических методов, которые не требует сведений о составе и структуре системы. В большинстве случаев построения модели реального процесса аналитику приходится иметь дело с выборками малого объема, причем в пространстве наблюдений результаты измерений распределены неравномерно. Этот факт часто вызван большими затратами на проведение экспериментов для снятия наблюдений, отсутствием возможности проводить дополнительные эксперименты в случае нормального функционирования объекта либо отсутствием возможности повторить эксперимент при одних и тех же условиях. Это приводит к тому, что в некоторых подобластях пространства наблюдений образуются «пустоты». В данных условиях построение стандартной непараметрической оценки регрессии дает неудовлетворительные результаты.
Пусть имеется неравномерная выборка наблюдений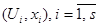 
входных и выходных переменных системы объемом s. Здесь 
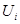- значение вектора наблюдений входных воздействий размерности m в i-ой точке выборки, а xi - значение выходного воздействия в этой точке. Требуется построить непараметрическую модель объекта на основе непараметрической оценки регрессии, имеющей следующий вид [1]:
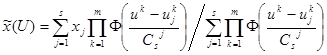, (1)
где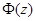 
- колоколообразная функция, удовлетворяющая следующим условиям [1]:
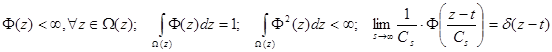, (2)
здесь δ(t) - дельта-функция Дирака. Параметр размытости Сs должен удовлетворять следующим условиям [1]:
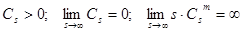(3)
Предлагается использовать непараметрическую оценку регрессии, основанную на использовании не конкретного значения выходной переменной в j-ой точке выборки, а ее оценки. Проводить это оценивание будем по нижеизложенному алгоритму.
Пусть мы находимся в i-ой точке выборки, определяются соседние точки выборки, в которых колоколообразная функция не равна нулю:
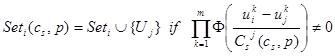, (4)
где колоколообразная функция:
,
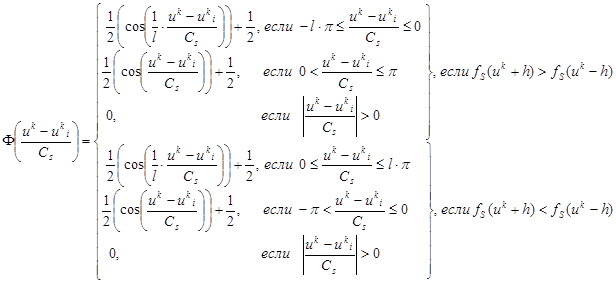расширяется в направлении разрежений в выборке, то есть ее ветви имеют разные константы Липшица. Здесь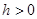 
- шаг, 
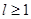– коэффициент «расширения» колоколообразной функции, при l=1 колоколообразная функция принимает симметричный вид.
Для определения сгущений и разрежений точек в выборке введем функцию множества, которая имеет вид непараметрической оценки плотности Розенблата-Парзена [2] с малым параметром размытости сs:
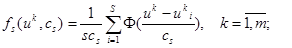(5)
Через точки (1) проводим поверхность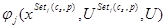 
, параметры которой определяются по методу наименьших квадратов.
Непараметрическая оценка регрессии примет следующий вид [3]:
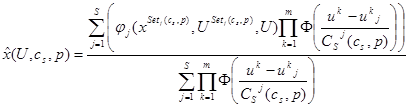. (6)
Чтобы оценить параметр размытости в этой формуле для j-ой точки выборки будем использовать следующую формулу:
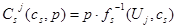. (7)
Выбор оптимального параметра размытости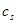 
и коэффициента пропорциональности p осуществляется путем минимизации критерия:
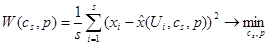. (8)
Приведем некоторые численные результаты моделирования.
Пусть имеется неравномерная выборка наблюдений случайной величины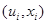 
, 
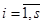, объемом s=30, 
, 
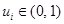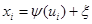, где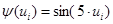 
, 
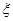- аддитивная центрированная помеха, имеющая нормальный закон распределения с 
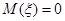и 
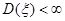. Расположение точек 
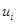на указанном интервале приведено на рисунке 1.
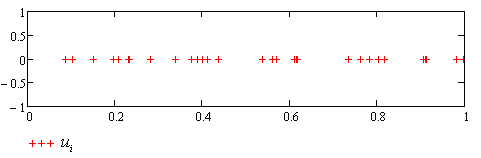
Рисунок 1
Пусть помехи в каналах измерения отсутствуют, а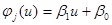 
имеет линейный вид, коэффициенты 
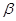определяются по методу наименьших квадратов на основании точек 
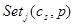. Результат моделирования приведен на рисунке 2.
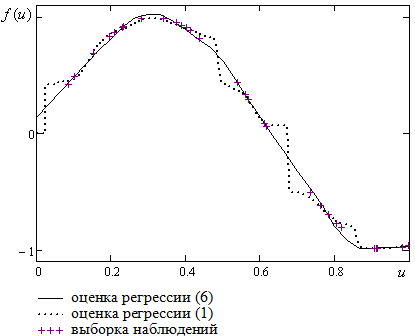
Рисунок 2
Очевидно, что оценка регрессии (1) в областях разрежений выборки дает неудовлетворительные результаты. Среднеквадратичная оценка ошибки моделирования равна 4,95%. При использовании модифицированной оценки регрессии (6) с несимметричной колоколообразной функцией оценка ошибки моделирования равна 2,25%.
Результаты моделирования при 15% помехе в каналах измерения и неизменных остальных условиях приведены на рисунке 3.
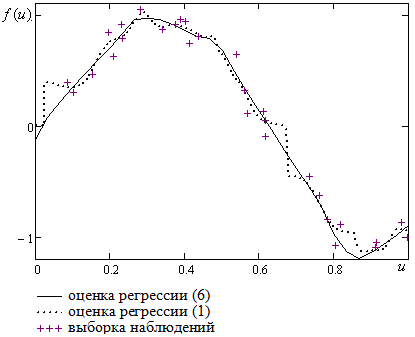
Рисунок 3
Среднеквадратичная оценка ошибки моделирования при использовании стандартной непараметрической оценки регрессии (1) равна 6%. При использовании модифицированной оценки регрессии с несимметричной колоколообразной функции оценка ошибки моделирования равна 4,4%.
Зависимость ошибки моделирования при использовании оценок регрессии (1) и (6) от уровня шума в % приведена на рисунке 4.
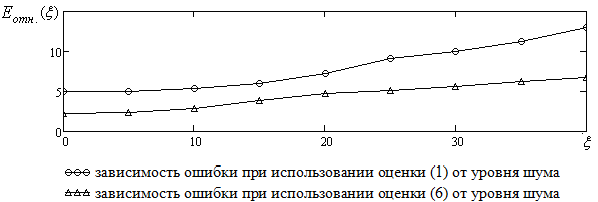
Рисунок 4
Таким образом, можно отметить, что ошибка моделирования при использовании модифицированной оценки регрессии (6) примерно в 2 раза меньше, чем при использовании стандартной непараметрической оценки (1).
Выберем другой объект с одномерным входным и выходным воздействиями. Для этого примем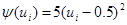 
. Объем выборки по-прежнему равен 30: 
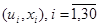. Пусть выборка наблюдений относительно равномерна и не имеет больших пробелов. Результаты моделирования приведены на рисунке 5.
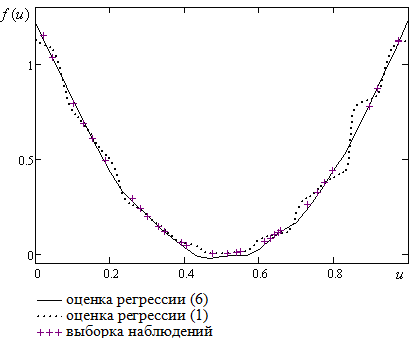
Рисунок 5
Среднеквадратичная оценка ошибки моделирования при использовании стандартной непараметрической оценки регрессии (1) равна 1,9%. При использовании модифицированной оценки регрессии (6) с несимметричной колоколообразной функции ошибка равна 0,77%, что в 2,5 раза меньше, чем при использовании стандартной оценки.
Таким образом, даже при разреженной выборке наблюдений, без явных пробелов ошибка моделирования с использованием модифицированной оценки регрессии (6) меньше, чем с использованием стандартной.
Пусть размерность входной переменной равна двум, и имеется неравномерная выборка наблюдений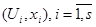 
, объемом s=200, 
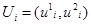, на области 
, 
; 
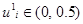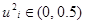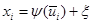, где 
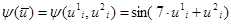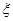, - аддитивная центрированная помеха, имеющая нормальный закон распределения с математическим ожиданием 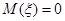и ограниченной дисперсией. Создадим пробел в выборке наблюдений. Расположение точек 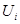приведено на рисунке 6.
Пусть в каналах измерения присутствует 5% помеха, а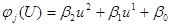 
имеет линейный вид (плоскость), где 
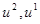- входные переменные. Графически результат моделирования в виде среза представлен на рисунке 7.
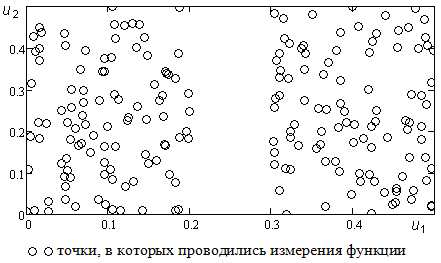
Рисунок 6
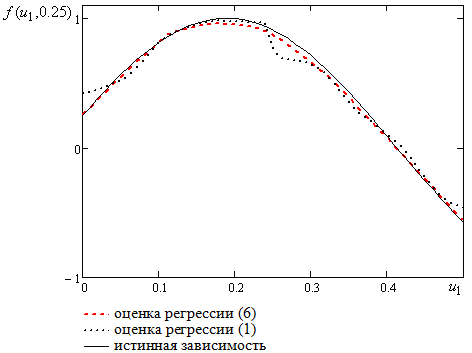
Рисунок 7
Среднеквадратичная оценка ошибки моделирования при использовании стандартной непараметрической оценки регрессии (1) равна 3,3%. При использовании модифицированной оценки регрессии (6) с несимметричной колоколообразной функции оценка ошибки равна 1,5%, что в 2 раза меньше, чем при использовании стандартной оценки.
Пусть имеется неравномерная выборка наблюдений одномерных входного и выходного воздействий объекта 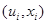, , 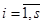объемом s=30, 
, 
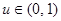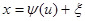, где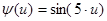 
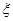, - центрированная помеха, распределенная нормально с нулевым математическим ожиданием и ограниченной дисперсией. Пусть функция 
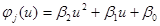имеет квадратичный вид. Помеха в каналах измерения 10%.
Результаты моделирования приведены на рисунке 8.
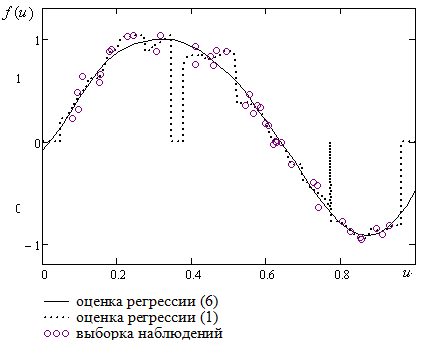
Рисунок 8
При построении модели этого же объекта, но производя аппроксимацию линейным полиномом 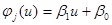, среднеквадратичная ошибка моделирования в 1,9 раза больше, чем при аппроксимации квадратичным полиномом. При дальнейшем увеличении порядка аппроксимирующего полинома ошибка моделирования практически не изменяется, а при порядках полинома больше 4 ошибка моделирования увеличивается. Таким образом, предлагается использовать второй порядок аппроксимирующего полинома 
.
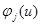Были проведены численные исследования алгоритмов непараметрического моделирования (1) и (6) на равномерных выборках наблюдений, а также сравнение ошибок моделирования при использовании симметричной и несимметричной колоколообразных функций.
Подведем итоги проведенных численных исследований.
Во-первых, разработанный метод построения непараметрических моделей позволяет довольно эффективно проводить моделирование процессов и объектов в случае неравномерно распределенной выборки наблюдений входных и выходных переменных, что подтверждают численные исследования приведенные выше. Среднеквадратичная ошибка моделирования при использовании непараметрической оценки регрессии (6) с несимметричной колоколообразной функции в несколько раз меньше, чем при использовании оценки регрессии (1).
Во-вторых, применение несимметричной колоколообразной функции позволяет добиться большей согласованности модели и объекта, по сравнению с симметричной.
В-третьих, с увеличением помехи в каналах измерения выходной переменной ухудшается качество моделирования. Однако ошибка моделирования при использовании модифицированной оценки регрессии (6) все же остается в несколько раз меньше, чем при использовании стандартной оценки (1).
В-четвертых, применение вышеупомянутых оценок регрессии для моделирования на основе равномерной выборки наблюдений входных и выходных переменных объекта дает одинаково малые ошибки идентификации. Следовательно, модифицированную оценку регрессии можно применять не только на неравномерных или разреженных выборках, но и на равномерных.
В заключение стоит отметить, что при увеличении размерности входной переменной на единицу время расчета модели при использовании модифицированной непараметрической оценки регрессии с несимметричной колоколообразной функцией увеличивается в среднем в полтора раза при фиксированном объеме выборки наблюдений.
Библиографический список
1. Надарая Э.А. Замечания о непараметрических оценках плотности вероятности и кривой регрессии / Э.А. Надарая // Теория вероятности и ее применение.- Т. 15, вып. 1, 1970.-с. 139-142.
2. Парзен Е. (Parzen E.). On estimation of a probability density function and mode.—Ann. Math. Stat., 1962, v. 33, 1065— 1076.
3. Катковник В.Я. Непараметрическая идентификация и сглаживание данных / В.Я. Катковник М.: Наука, 1985. 427с.
