Анализ методов распознавания образов



Существует множество методов распознавания образов на изображениях. Понимание данных методов важно для решения различного рода задач.

Во-первых, важно понимание теории распознавания образов. Основными терминами являются:

Класс — множество объектов, имеющие общие свойства. Классов может быть неограниченное количество.

Классификация — процесс назначения меток класса объектам, согласно некоторому описанию свойств этих объектов.

Классификатор — устройство, которое в качестве входных данных получает набор признаков объекта, а в качестве результата выдающий метку класса.

Верификация — процесс сопоставления экземпляра объекта с одной моделью объекта или описанием класса.

Признак — количественное описание того или иного свойства исследуемого предмета или явления.

Пространство признаков — это N-мерное пространство, определенное для данной задачи распознавания, где N — фиксированное число измеряемых признаков для любых объектов. Вектор из пространства признаков x, соответствующий объекту задачи распознавания это N-мерный вектор с компонентами (x_1,x_2, …,x_N), которые являются значениями признаков для данного объекта.

Таким образом, вся задача распознавания сводится к выделению существенных признаков для каждого класса и, в конечном итоге, отнесение входных данных к одному из них посредством обнаружения ключевых признаков в исходном изображении. То есть распознавание образов можно разделить на несколько задач, таких, как:

1. Получение входных данных, с помощью сенсоров, камер видеонаблюдения, подборок данных.
2. Первичная обработка изображений такая, как нормализация данных, фильтрация шумов, выявление признаков.
3. Формирование векторов признаков, посредством выбора наиболее значимых признаков, с помощью которых можно выделить непересекающиеся множества классов.
4. Классификация или предсказание на основе полученных данных о классах.

Данные этапы представлены на рисунке 1.

Рис. 1. Этапы задачи распознавания.

Примерами задач классификации являются:

‒ распознавание символов;

‒ распознавание речи;

‒ установление медицинского диагноза;

‒ прогноз погоды;

‒ распознавание лиц

‒ классификация документов и др.

Например, рассмотрим 2 класса объектов: небоскреб и загородный дом. В качестве признаков можно выбрать высоту и материалы (дерево или стекло). Как следует из рисунка (x1-высота, х2-материалы), эти два класса образуют два непересекающихся множества. Однако не всегда удается выбрать правильные измеряемые параметры в качестве признаков классов. Например выбранные параметры не подойдут для создания непересекающихся классов офиса и жилого здания.

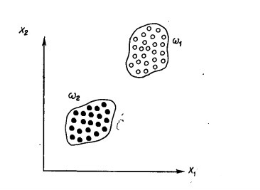
Рис. 2. Евклидово пространство признаков двух классов

Таким образом — первая проблема распознавания — нахождение таких признаков, которые четко разделяют пространство на классы.

Следующей задачей распознавания является исключение межклассовых признаков, которые не несут в себе никакой полезной информации для классификации и только создают избыточную нагрузку на вычислительные ресурсы.

Далее необходимо выявить оптимальную решающую процедуру. Так как на данном этапе мы имеем n классов и измерительные векторы для каждого из них, то задачу можно свести к построению границ, разделяющих классы.

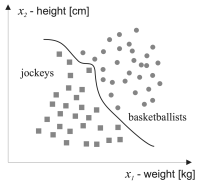
Рис. 3. Границы, разделяющие классы в евклидовом пространстве

Сравнение объектов можно производить на основе их представления в виде векторов измерений. Данные измерений удобно представлять в виде вещественных чисел. Тогда сходство векторов признаков двух объектов может быть описано с помощью евклидова расстояния.

Разделяют 3 группы методов распознавания образов:

‒ Сравнение с образцом. К этой группе относятся структурные методы и методы, использующие приближение и расстояние (классификации по ближайшему среднему и по расстоянию до ближайшего соседа.)

‒ Статистические методы. Примером этой группы служит байесовский метод принятия решения. Статистические методы основаны на вычислении вероятности.

‒ Нейронные сети. Отдельный класс методов распознавания. В отличие от других методов, нейронные сети способны обучаться уже в процессе распознавания и обладают хорошим потенциалом развития.

Далее рассмотрим различные методы, относящиеся к разным группам.

Метод 1. Классификация по ближайшему среднему значению

В классическом подходе к системам распознавания вектор признаков, характеризующий каждый класс, получается в следствие обучения системы и известен заранее или на основе каких-либо моделей предсказывается в режиме реального времени.

Один из самых простых алгоритмов классификации использует вектор математического ожидания класса (среднее значение).

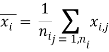
– j-й эталонный признак класса i, – количество эталонных векторов класса i.

Следовательно, неизвестный объект будет относиться к классу i, если он существенно ближе к вектору математического ожидания класса i, чем к векторам математических ожиданий других классов. Такой метод применим, когда точки признаков расположены очень кучно и далеко от точек других классов.

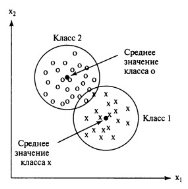
Рис. 4. Классификация по ближайшему среднему значению

Ниже приведен пример ситуации, когда данный метод не будет работать. Как видно, класс 2 разделен на два непересекающихся множества признаков, а класс 3 слишком вытянут, что приводит к ситуации, когда его удаленные точки ближе к среднему значению другого класса, нежели к его собственному среднему значению.

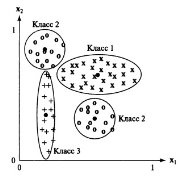
Рис. 5. Недостатки метода классификации по ближайшему среднему значению

Описанная проблема в некоторых случаях может быть решена изменением расчета расстояния.

Будем учитывать характеристику «разброса» значений класса –, вдоль каждого координатного направления i. Среднеквадратичное отклонение равно квадратному корню из дисперсии. Шкалированное евклидово расстояние между вектором x и вектором математического ожидания равно

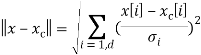
Эта формула расстояния позволяет уменьшить количество ошибок классификации, но на деле большинство задач не удается представить таким простым классом.

Метод 2. Классификация по расстоянию до ближайшего соседа

Этот метод относит неизвестный вектор признаков к классу, отдельные образцы которого находятся ближе всех. Такие образцы называются ближайшими соседями. При классификации по ближайшему соседу не требуется знать моделей распределения классов в пространстве, необходима только информация об эталонных образцах.

Принцип работы алгоритма построен на определении минимального расстояния до образца признака из базы данных. Так же решение можно улучшить, если искать среди соседей. Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции:

‒ Вычислить расстояние до каждого из объектов обучающей выборки

‒ Отобрать k объектов обучающей выборки, расстояние до которых минимально

‒ Класс классифицируемого объекта — это класс, наиболее часто встречающийся среди k ближайших соседей

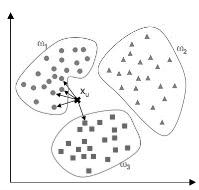
Рис. 6. Классификация по расстоянию до ближайшего соседа

Преимущества такого подхода очевидны:

‒ в любой момент можно добавить новые образцы в базу данных;

‒ древовидные и сеточные структуры данных позволяют сократить количество вычисляемых расстояний.

Данный алгоритм — один из простейших алгоритмов классификации, поэтому на реальных задачах он зачастую оказывается неэффективным. Помимо точности классификации, проблемой этого классификатора является скорость классификации: если в обучающей выборке N объектов, в тестовом выборе M объектов, а размерность пространства — K, то количество операций для классификации тестовой выборки может быть оценено как O(K*M*N).

Метод 3. Структурный.

Такой метод распознавания применяется для объектов, которые можно структурно разделить на составляющие. Так же важно, чтобы при распознавании система нашла такие признаки, которые точно позволяют сказать, что объект относится к этому классу и к никакому другому.

Как пример использования, можно привести задачу распознавания начертательных символов или фигур.

Второе название этого метода — синтаксический, так как он подразумевает использование языка описания образов, который структурно описывает каждый элемент и подэлемент, структурно разделяя образ на подобразы. Метод будет полезен для распознавания сложных образов, состоящих из многих образов более низкого, простого уровня.

На рисунке 7 показан пример структурного распознавания двух различных геометрических фигур. В рамках такого подхода распознавания образов считается, что они состоят из отдельных подобразов, соединенных различными способами.

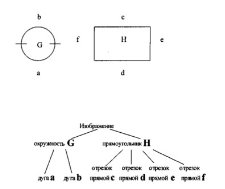
Рис. 7. Структурный метод распознавания

Таким образом круг состоит из двух дуг, а прямоугольник из четырех отрезком прямых. Данная классификация позволяет однозначно определить принадлежность объекта к одному из классов.

Метод 4. Байесовский подход к принятию решения

Данный метод основан на теореме Байеса и определении априорных вероятностей, то есть вероятность исходов или принадлежности объекта определенному классу изменяется после получения новых экспертных оценок (подтверждения наличия новых признаков).

Появление того или иного образа является случайным событием и вероятность этого события можно описать с помощью закона распределения вероятностей многомерной случайной величины ξ в той или иной форме. Зная элементы обучающей выборки можно восстановить вероятностные характеристики этой среды.

Байесовский классификатор на основе наблюдаемых признаков относит объект к классу, к которому этот объект принадлежит с наибольшей вероятностью. Как уже отмечалось, в основе метода лежит теорема Байеса. Предположим, что мы рассматриваем некоторую случайную величину X, которая имеет плотность вероятности p(x,w) с параметром w. Но нам нужно получить данные о другой случайной величине w, имеющей некоторое распределение вероятности τ(w). Пусть в результате наблюдений получены статистические данные x. Из определения условной вероятности следует:

Так же из этого же определения следует, что:

Подставив второе выражение в первое получим формулу Байеса

Для нашей задачи имеется m классов, т. е. m возможных переменных (…), соответственно формула Байеса примет вид:

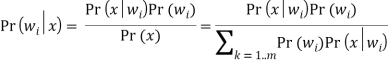
Распределение Pr(w) называют априорным распределением вероятностей возможных значений w. Данное распределение известно прежде, чем будут получены статистические данные, то есть новые признаки (экспертные оценки).

Распределение – апостериорное распределение значений w, при условии получения статистических данных. Здесь — гипотеза, а x — свидетельство, поддерживающее гипотезу. Если все классы характеризуются собственными несовместными вероятностями, охватывающими все возможные случаи, то можно применить правило Байеса для вычисления апостериорных вероятностей каждого класса по априорным вероятностям этих классов и распределениям условной вероятности для x.

На практике необходимо каким-то образом обеспечить вычисление . Эмпирический подход предполагает разбиение диапазона х, на интервалы, затем подсчет частот появления х среди значений каждого интервала и построение гистограммы на основе этих измерений.

Обычно используется распределения Пуассона, экспоненциальное и нормальное.

Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами μ и σ^2, если ее плотность вероятности имеет вид:

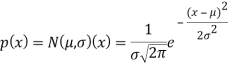
Пример распределения Гаусса для различных параметров µ и σ показан ниже

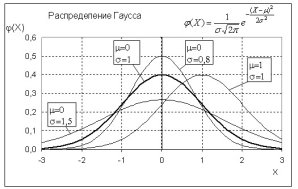
Рис. 8. Нормальное распределение Гаусса

Приведем пример использования теоремы Байеса для распознавания образов:

Предположим, что есть выборка апельсинов. Какова вероятность того, что m-й апельсин, который не принадлежит нашей выборке будет вкусным, при условии того, что мы измерили размер и цвет? В теории вероятностей данную предпосылку можно записать так, использую теорему Байеса:

В данной формуле Х — посылка, а Y — следствие. Переход от посылки к следствию подчиняется вероятностным законам, то есть принимает значения от 0 до 1. Рассмотрим правую часть этого выражения более подробно. — априорная вероятность, которая обозначает возможность встретить вкусный апельсин среди всех возможных. Априорная вероятность встретить невкусный апельсин — . Мы можем оценить априорную вероятность исходя из статистики, например нам известно, что по прошлому опыту 50 % апельсинов вкусные. — показывает, насколько вероятно получить конкретное значение цвета и размера для апельсина класса 1, данная вероятность может быть представлена в виде нормального закона распределения. Это выражение так же называется функцией правдоподобия. — знаменатель нужен для того, чтобы искомая вероятность изменялась в пределах 0 и 1.

Наше решение зависит от тех параметров, которые мы знаем. Например, мы можем знать только значения априорной вероятности, а остальные значения оценить невозможно. Тогда решающее правило будет такое — ставить всем апельсинам значение того класса, для которого априорная вероятность наибольшая. Таким образом, если мы знаем, что 80 % всех апельсинов в природе вкусные, то мы ставим всем апельсинам класс 1, наша вероятность ошибки будет 20 %. Если же мы все же сможем подсчитать значение функции правдоподобия, то и сможем найти значение искомой вероятности по формуле Байеса. Решение здесь будет таким — поставить метку того класса, для которого вероятность — максимальна.

Таким образом недостаток данного метода заключается в том, что в нашем случае мы представляем объект парой чисел — цвет и размер, но в более сложных задачах размерность признаков может быть в разы выше и для оценки вероятности многомерной случайной величины может не хватить числа наблюдений из списка с историческими данными.

Метод 5. Нейронные сети

Нейроные сети позволяют решать широкий круг задач и представляют из себя структуру из нескольких слоев — искусственных нейронов(вычислительных элементов) и связей между ними. Структура имитирует структуру и свойства организации нервной системы живых организмов. Нейросеть получает на вход набор сигналов и на выходе выдает соответствующий ответ (выходные сигналы), которые описывают решение некоторой задачи. Ниже представлена схема нейросети:

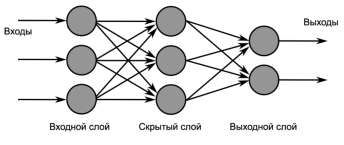
Рис. 9. Структура нейронной сети

Чтобы описать принцип работы сети, представим искусственный нейрон, схема которого изображена ниже:

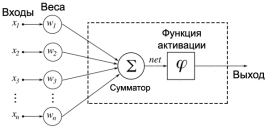
Рис. 10. Структура искусственного нейрона

Соответственно на каждый нейрон входного слоя поступает сигнал, который умножается на соответствующий ему вес. Функция активации представляет собой либо пороговое значение, передающее на выход единичный сигнал, либо сигмоидальной функцией, которая преобразовывает значение суммы всех пришедших сигналов, в число, находящееся в диапазоне от 0 до 1.

Таким образом на выходе сети получается вероятностное значение, похожее на результат метода Байеса.

По сравнению с линейными методами статистики, нейросети позволяют эффективно строить нелинейные зависимости, более точно описывающие наборы данных. Что же касается байесовского классификатора, строящего квадратичную разделяющую поверхность, нейронная сеть может построить поверхность более высокого порядка. Высокая нелинейность разделяющей поверхности наивного байесовского классификатора (он не использует ковариационные матрицы классов, как классический Байес, а анализирует локальные плотности вероятности) требует значительного суммарного числа примеров для возможности оценивания вероятностей при каждом сочетании интервалов значений переменных − тогда как нейросеть обучается на всей выборке данных, не фрагментируя её, что повышает адекватность настройки сети.

В данной статье были изучены методы, применяемые для распознавания изображений. Автор пришел к выводу, что выбор метода в первую очередь зависит от исходной задачи, однако нейронные сети являются наиболее перспективным направлением в данный момент и покрывают наибольшее количество задач.

Литература:

1. Местецкий Л. В. Математические методы распознавания образов. Курс лекций.. — М.:, 2004. — 85 с.
2. Пару слов о распознавании образов // Хабрахабр.
3. URL: https://habrahabr.ru/post/208090/.
4. Л. П. Попова, И. О. Датьев. Обзор существующих методов распознавания образов. — М.: Сборник научных трудов, 2007. — 11 с.
5. R. Polikar. Pattern Recognition. — Glassboro, New Jersey:,. — 21 с. R. Duin, E. Pekalska. Pattern Recognition