Алгоритм Лерча — Гроссмана и его реализация на центральном и графическом процессорах

ВВЕДЕНИЕ

Ограниченность минеральных и органических образований на нашей планете, их несоизмеримый период естественного воспроизводства относительно нарастающих темпов развития мировой промышленности, а так же современная проблема исчерпания природных ресурсов, привела к насущной потребности комплексного извлечения и рационального использования полезных ископаемых. [1]. Горные предприятия ориентированы на четком планировании горных работ, что прямым образом сказывается на максимизации получаемой прибыли конкретного месторождения.

Прикладная математика нашла ответы на непростые вопросы горнодобывающей отрасли, такие как моделирование месторождения на основании данных опробования, и нахождение предельных контуров открытого карьера. Для решения первого вопроса применяются методы пространственной интерполяции, а второго методы, основанные на теории графов. В данной статье приводится описание применения алгоритма нахождения оптимального карьера Лерча-Гроссмана, основанное на теории графов.

Проектирование открытого карьера, можно произвести разными методами, однако одним из наиболее результативных является алгоритм Лерча-Гроссмана. Единственным существенным недостатком алгоритма является время его работы. Тем не менее методы построения карьеров, которые акцентируют внимание на сокращении времени работы алгоритма, теряют точность вычислений. В соответствии с сложившейся ситуацией на рынке решений для горнодобывающей отрасли, алгоритм Лерча-Гроссмана является наиболее востребованным алгоритмом построения открытого карьера.

Альтернативные методы построения открытого карьера.

Проектирование открытого карьера можно рассматривать как процесс оптимизации, когда чистая приведенная стоимость месторождения увеличивается до максимально-возможного значения. Чистая приведенная стоимость — это показатель экономической эффективности вовлечения инвестиций в разработку месторождения. [2]. Процедура построения открытого карьера для месторождения, чистая приведенная стоимость которого равна максимально-возможному значению, происходит благодаря алгоритмам построения открытого карьера.

Пикард и Керан, предложили решение проблемы минимального разреза методом квадратичного программирования, которое оказало большое влияние в определении оптимального контура бортов открытого карьера.

Чжао и Ким, представили алгоритм, основанный на теории графов для определения оптимального открытого карьера, которому необходимо меньше компьютерных ресурсов относительно алгоритма Лерча-Гроссмана.

Хочбаум и Чэнь, рассматривали проблему нахождения оптимального открытого карьера, принимая во внимание подробные экономические данные и вопросы инженерного снабжения.

Лерч и Гроссман, создали первый метод оптимизации, который можно было применить в построении больших открытых карьеров за разумное время работы. Метод Лерча-Гроссмана широко используется в программном обеспечении для проектирования открытых карьеров, как промышленный стандарт. [3].

Определение предельного контура открытого карьера считается одной из основных проблем горнодобывающей отрасли. Данные предельного контура карьера предоставляют информацию, необходимую в оценке экономического потенциала месторождения полезных ископаемых, а также необходима для формирования долгосрочных, промежуточных и ближайших планов открытой разработки месторождения. Для решения этой задачи было предложен ряд математических методов, наиболее оптимальным среди которых является алгоритм Лерча-Гроссмана. Алгоритм Лерча-Гроссмана является полноценным алгоритмом, который производит процедуру нахождения предельного контура открытого карьера, начиная от блочной модели месторождения и заканчивая оптимальным открытым карьером, а также он не зависит от каких-либо других методов. [4].

Алгоритм Лерча-Гроссмана.

Алгоритм построения открытого карьера Лерча-Гроссмана — это первый подобный алгоритм, который начали применять в практике на больших месторождениях. Алгоритм основан на теории графов, и за разумные сроки по времени позволяет определить предельный контур открытого карьера. Цель алгоритма Лерча-Гроссмана заключается в процедуре разработки такого контура открытого карьера, который увеличивает разницу между общей стоимостью содержания полезного компонента в месторождении, и стоимостью добычи полезного и неполезного компонентов месторождения. [3]. В процессе работы алгоритма Лерча-Гроссмана создается граф модели месторождения и показывается, что оптимальное решение задачи нахождения предельного контура открытого карьера заключается в поиске конечного контура на графе модели месторождения.

Далее описано решение задачи определения максимального конечного контура открытого карьера, которая первоначально была предложена математиками Лерчем и Гроссманом.

Графу модели месторождения 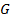, добавляется фиктивный узел 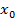, и фиктивные арки 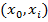. Узлу  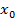присваивается отрицательный вес, для того чтобы он не входил в максимальный конечный контур. Дерево  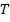с выделенным узлом  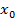(называемым корнем 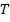), является корневым деревом. Работа алгоритма начинается с построения дерева  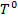в графе 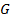. Построенное дерево в дальнейшем последовательно преобразуется в деревья 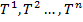, следуя установленным правилам, пока дальнейшее последовательное преобразование будет невозможным. В результате искомый максимальный конечный контур содержит хорошо определенные ветви полученного дерева. [5].

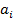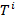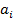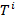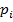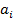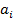Каждая арка  дерева определяет ветвь . Арка  поддерживает ветвь . Вес  ветви является суммой весов всех узлов ветви. Этот вес ассоциируется с , а  поддерживает вес 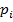. В дереве  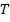с корнем 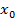, ветка  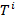характеризуется ориентацией арки  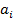относительно корня 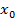. Арка  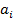называется p-аркой (положительной аркой), если она направлена в сторону 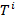, т. е. если конечный узел  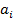является частью 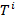. Тогда ветка  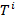называется p-веткой (положительной веткой). Если  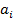направлена в противоположную сторону от 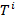, тогда она называется m-аркой (отрицательной аркой), а ветка называется m -веткой (отрицательной веткой).

P-арка (ветка) называется сильной, если она поддерживает положительный вес. M-арка (ветка) называется сильной, если она поддерживает вес, который равен нулю или отрицателен. Арки (ветви), которые являются не сильными, называются слабыми. Узел 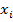 является сильным, если на пути следования к корню  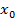дерева 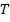, находится хотя бы одна сильная арка. Узлы, которые являются не сильными, называются слабыми. В итоге дерево называется нормализованным, если корень  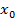является общим для всех сильных арок. Максимальный конечный контур, нормализованного дерева — это, набор сильных узлов.

Рис. 1. Граф модели месторождения, с добавленным фиктивным узлом

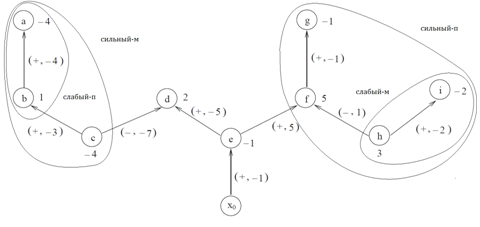
Рис. 2. Сильные и слабые ветви

Чтобы проиллюстрировать эти понятия, рассмотрим граф модели месторождения изображенный на рисунке 1. Значения, присвоенные каждому узлу, являются весом этого узла. Каждая арка помечена в формате 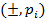 для определения состояния. Здесь знак 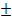, представляет p-арку или m-арку соответственно, и  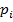это вес поддерживаемый аркой. При раскрытии метки арки, мы можем выяснить состояние (сильный или слабый). 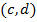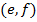Арки  и  являются сильными, а все остальные слабыми. 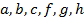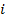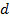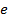Поэтому, узлы  и  являются сильными, когда  и  являются слабыми. Иллюстрация сильных и слабых веток показана на рисунке 2. На рисунке 3 представлено дерево, полученное после нормализации. Заметим, что все фиктивные арки являются p-арками, все сильные арки нормализованного дерева также должны быть p-арками.

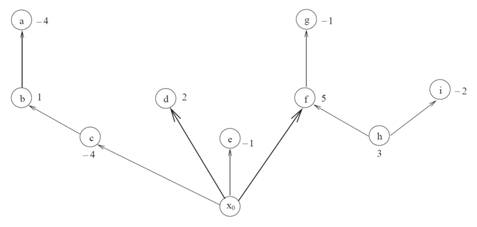
Рис. 3. Дерево, полученное после нормализации

Следом приведены шаги необходимые для нахождения максимального конечного контура [6].

Шаг 1 — Инициализация.

Построить нормализованное дерево .  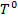берется в качестве связующего дерева (дерево максимального набора арок, которое не содержит циклов) набор арок, который 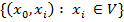. Определить набор  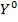сильных узлов  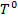(узлы, имеющие положительный вес). Установить 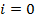, и перейти к шагу 2.

Шаг 2 — Тестирование оптимальности.

Поиск арки 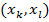 в графе  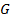такой, что  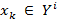и 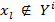 далее переходим к шагу 3. Если такой арки не будет найдено, необходимо остановить работу, следовательно,  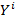является максимальным конечным контуром графа .

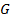Шаг 3 — Обновление.

Определить уникальный 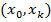 путь 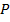, в ветви 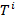. Пусть  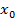связан с 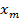, на пути 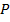. Построить дерево 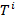, заменив  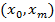ветки 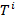 на арку 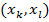, и перейти к шагу 4.

Шаг 4 — Нормализация.

Нормализовать дерево 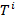. В результате получим дерево 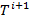. Определить набор  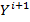сильных узлов дерева 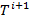, и перейти к шагу 2.

Отметим, что 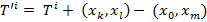. Нормализованное дерево 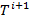, получается путем перемещения вдоль уникального  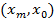пути, и если встретится сильный узел — он будет удален, а  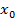переходит к корневой ветви дерева 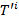. Таким образом, полученный максимальный конечный контур является предельным конечным контуром, что и является оптимальным открытым карьером.

Реализация алгоритма Лерча-Гроссмана

Рассмотрим более подробно реализацию алгоритма Лерча-Гроссмана на CPU и GPU. Блок-схема алгоритма Лерча-Гроссмана на CPU приведена на рисунке 4.

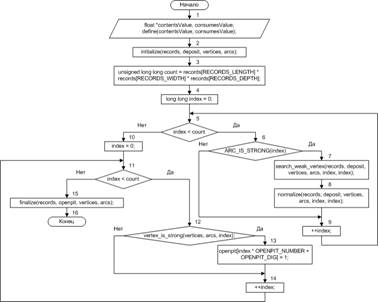
Рис. 4. Алгоритм Лерча-Гроссмана на CPU

Описание к блок-схеме алгоритма Лерча-Гроссмана на CPU:

1.         производится расчет весов всех вершин, входящих в модель месторождения;

2.         создаются две структуры: структура вершины, которая содержит значения рассчитанных весов, и структура арки, которая содержит знак («+» или «-») и вес, начало арки изначально находится в корневой вершине и конец арки, находящийся в текущей вершине;

3.         рассчитывается общее количество вершин, содержащихся в модели месторождения;

4.         производится инициализация переменной, указывающей на перебираемую вершину;

5.         проверка выхода за предел общего количества вершин, содержащихся в модели месторождения. Если условие верно, то переходим к пункту 6, если нет, к пункту 10;

6.         проверка, является ли арка перебираемой вершины сильной аркой. Если да, то переходим к пункту 7, если нет, к пункту 9;

7.         производится поиск слабой вершины, которая входит в конус, строящийся при извлечении текущей сильной вершины. Началу арки слабой вершины, которая была найдена, присваивается адрес текущей сильной вершины, а также производится перерасчет веса данной арки;

8.         производится процедура нормализации ветви, расположенной между текущей сильной вершиной и найденной слабой вершиной;

9.         производится переход к следующей вершине;

10.     производится инициализация переменной, указывающей на перебираемую вершину;

11.     проверка выхода за предел общего количества вершин, содержащихся в модели месторождения. Если условие верно, то переходим к пункту 12, если нет, к пункту 15;

12.     проверка, является ли перебираемая вершина сильной. Если да, то переходим к пункту 13, если нет, к пункту 14;

13.     отмечаем перебираемую вершину на извлечение;

14.     производится переход к следующей вершине;

15.     удаление структур, вершины и арки;

16.     все отмеченные на извлечение вершины, образуют предельный контур карьера.

Блок-схема алгоритма Лерча-Гроссмана на GPU приведена на рисунке 5.

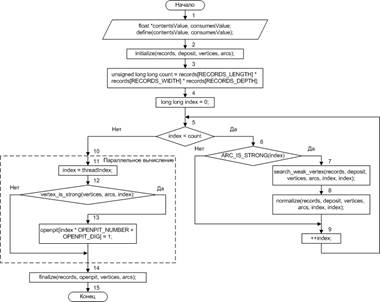
Рис. 5. Алгоритм Лерча-Гроссмана на GPU

Описание к блок-схеме алгоритма Лерча-Гроссмана на GPU:

1.         производится расчет весов всех вершин, входящих в модель месторождения;

2.         создаются две структуры: структура вершины, которая содержит значения рассчитанных весов, и структура арки, которая содержит знак («+» или «-») и вес, начало арки изначально находится в корневой вершине и конец арки, находящийся в текущей вершине;

3.         рассчитывается общее количество вершин, содержащихся в модели месторождения;

4.         производится инициализация переменной, указывающей на перебираемую вершину;

5.         проверка выхода за предел общего количества вершин, содержащихся в модели месторождения. Если условие верно, то переходим к пункту 6, если нет, к пункту 10;

6.         проверка, является ли арка перебираемой вершины сильной аркой. Если да, то переходим к пункту 7, если нет, к пункту 9;

7.         производится поиск слабой вершины, которая входит в конус, строящийся при извлечении текущей сильной вершины. Началу арки слабой вершины, которая была найдена, присваивается адрес текущей сильной вершины, а также производится перерасчет веса данной арки;

8.         производится процедура нормализации ветви, расположенной между текущей сильной вершиной и найденной слабой вершиной;

9.         производится переход к следующей вершине;

10.     начало параллельного участка кода;

11.     производится инициализация переменной, указывающей на рассматриваемую вершину;

12.     проверка, является ли рассматриваемая вершина сильной. Если да, то переходим к пункту 13, если нет, к пункту 14;

13.     отмечаем рассматриваемую вершину на извлечение;

14.     удаление структуры вершины, и структуры арки;

15.     отмеченные вершины составляют предельный контур карьера.

Вывод

Процедура оптимизации построения открытого карьера, может быть произведена методом целочисленного программирования. Однако реализация такого вида программирования имеет определенные трудности, влияющие на сложность реализации метода и на ограниченность количества блоков блочной модели месторождения участвующих в расчете. Принимая во внимание эти практические трудности, решение задачи нахождения предельного контура открытого карьера на большинстве горнодобывающих предприятиях разделяют на три основных этапа. Основополагающим этапом является генерирование оптимального предельного контура открытого карьера методом Лерча-Гроссмана, который описан в этой статье. Далее, в полученном ранее максимальном конечном контуре создаются вложенные конечные контуры, путем изменения потенциала арок между узлами графа, данный процесс называется параметризацией открытого карьера. На третьем этапе, вложенные предельные контуры комбинируются для получения проекта препятствий, а затем эта информация вносится в график производства горнодобывающего предприятия.

Литература:

1.                  Закон Республики Казахстан о недрах и недропользовании, статьи 107–115, 2010 год.

2.                  Чистая приведенная стоимость, статья из сайта Wikipedia, https://ru.wikipedia.org/wiki/ Чистая_приведенная_стоимость.

3.                  H. Amankwah, Mathematical optimization models and methods for Open-Pit Mining, страницы 12–15, 2011 год.

4.                  H. Lerchs и I. F. Grossmann, Optimum design of Open-Pit Mines, страницы 51–54, 1965 год.

5.                  L. Caccetta и L. M. Giannini, An application of discrete mathematics in the design of an Open-Pit Mine, страницы 9–13, 1988 год.

6.                  N. Stuart, An introduction of the theory of Open-Pit Optimization, статья из сайта Resource Dynamics, http://www.agt.net/public/nstuart/pan/main.htm