Распределение Хотеллинга и его применение
Автор: Матинян Арам Артурович
Рубрика: 1. Математика
Опубликовано в
X международная научная конференция «Исследования молодых ученых» (Казань, май 2020)
Дата публикации: 04.05.2020
Статья просмотрена: 1564 раза
Библиографическое описание:
Матинян, А. А. Распределение Хотеллинга и его применение / А. А. Матинян. — Текст : непосредственный // Исследования молодых ученых : материалы X Междунар. науч. конф. (г. Казань, май 2020 г.). — Казань : Молодой ученый, 2020. — С. 1-5. — URL: https://moluch.ru/conf/stud/archive/370/15815/ (дата обращения: 20.09.2024).
В статье представлено статистическое расстояние и ее отличие от Евклидова расстояния (по прямой линии). Далее представляется одномерная ![]() -статистика Стьюдента и ее обобщение — статистика
-статистика Стьюдента и ее обобщение — статистика ![]() Хотеллинга. В заключение показано ее применение на практическом примере.
Хотеллинга. В заключение показано ее применение на практическом примере.
Ключевые слова: статистика Хотеллинга, статистическое расстояние, ингридиенты, ![]() статистика.
статистика.
Введение
На практике часто возникают проблемы, связанные с контролем многомерных статистических процессов. Хотя одномерные процессы контроля широко используются, но они не применяются, когда имеются изначально многомерные процессы. Здесь возникает необходимость использовать методы, позволяющие контролировать связь, существующую между переменными, описывающими процесс. Для выполнения этого статистика ![]() Хотеллинга дает необходимые методы.
Хотеллинга дает необходимые методы.
Эта статистика основана на идее статистического расстояния. Она сгруппировывает информацию, полученную с многомерного наблюдения и превращает ее в значение, которое является статистическим расстоянием этого наблюдения от среднего значения.
Статистическое расстояние
Предположим, имеется какой-то процесс. Обозначим наблюдение, полученное из процесса, состоящего из ![]() переменных в векторной форме, следующим образом:
переменных в векторной форме, следующим образом:
![]()
Наша задача — обработать информацию, имеющуюся в каждой из указанных
Предположим, мы получаем наблюдения вида ![]() из процесса, где
из процесса, где ![]() и
и ![]() — нескорелированные случайные величины. Представим точки
— нескорелированные случайные величины. Представим точки ![]() и
и ![]() в системе координат Декарта. Мы хотим знать, как далеко фиксированная точка находится от средней точки всех точек. Рассмотрим расстояние прямой линией (Евклидову), которая измеряет расстояние между двумя точками в соответствии с количеством единиц, разделяющих эти точки. Расстояние между фиксированной точкой
в системе координат Декарта. Мы хотим знать, как далеко фиксированная точка находится от средней точки всех точек. Рассмотрим расстояние прямой линией (Евклидову), которая измеряет расстояние между двумя точками в соответствии с количеством единиц, разделяющих эти точки. Расстояние между фиксированной точкой ![]() и средней точкой всех полученных точек
и средней точкой всех полученных точек ![]() будет дано формулой
будет дано формулой ![]() .
.
![]()
Обратите внимание, что мы взяли какую-либо точку ![]() и заменили ее каким-то числом —
и заменили ее каким-то числом — ![]() , которое является расстоянием между этой точкой и средней точкой.
, которое является расстоянием между этой точкой и средней точкой.
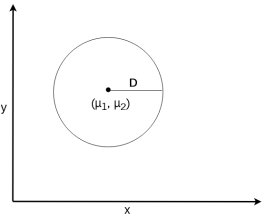
Если мы зафиксируем расстояние ![]() , то все точки, которые имеют расстояние
, то все точки, которые имеют расстояние ![]() от центра
от центра ![]() будут находиться на окружности с центром
будут находиться на окружности с центром ![]() и радиусом
и радиусом ![]() , а каждая точка, которая имеет меньшее расстояние от центра, чем
, а каждая точка, которая имеет меньшее расстояние от центра, чем ![]() , будет расположена внутри окружности (рис. 1).
, будет расположена внутри окружности (рис. 1).
![]()

Однако использование только Евклидова расстояния в большинстве статистических исследований недостаточно. Хотя каждая координата в равной степени участвует в определении расстояния по прямой линии, в этом случае изменение каждой из случайных величин в соответствии со стандартным отклонением ![]() не учитывается. Чтобы восполнить этот пробел, рассмотрим стандартизированные значения:
не учитывается. Чтобы восполнить этот пробел, рассмотрим стандартизированные значения:
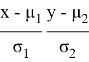
где ![]() и
и ![]() — соответственно стандартные отклонения
— соответственно стандартные отклонения ![]() и
и ![]() случайных величин. В случае таких значений формула расстояния примет вид
случайных величин. В случае таких значений формула расстояния примет вид ![]() .
.
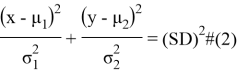
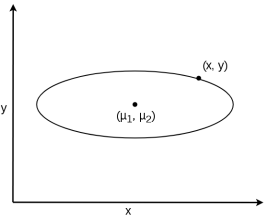
![]() называется статистическим расстоянием. Если мы зафиксируем
называется статистическим расстоянием. Если мы зафиксируем ![]() , то все точки, которые удовлетворяют уравнению
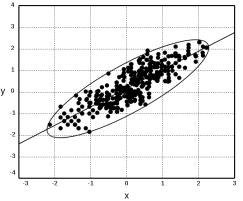
, то все точки, которые удовлетворяют уравнению ![]() , имеют одинаковое статистическое расстояние от заданного центра и у нас получается эллипс (рис. 2). Каждая точка в эллипсе имеет меньшее статистическое расстояние, чем
, имеют одинаковое статистическое расстояние от заданного центра и у нас получается эллипс (рис. 2). Каждая точка в эллипсе имеет меньшее статистическое расстояние, чем ![]() , и наоборот, каждая точка вне эллипса будет иметь статистическое расстояние больше, чем
, и наоборот, каждая точка вне эллипса будет иметь статистическое расстояние больше, чем ![]() .
.
Между прямой (Евклидовой) и статистическими расстояниями есть несколько важных различий. Давайте представим эти различия.
Первое отличие состоит в том, что случайные величины, используемые в формуле статистического расстояния, стандартизированы. Это важная особенность в многомерных процессах, так как случайные величины могут иметь разные единицы измерения. Следующее отличие состоит в том, что точки на эллипсе на рисунке 2 имеют одинаковое статистическое расстояние от центра, но могут иметь разные Евклидовы расстояния. В случае, если две переменные имеют равные дисперсии и они нескоррелированные, то статистические и Евклидовы расстояния равны с точностью до постоянного множителя, а в противном случае они отличаются друг от друга.
Основное различие между статистическими и Евклидовыми расстояниями состоит в том, что в противопоставление Евклидовому расстоянию каждая из случайных величин в статистическом расстоянии делится на свое стандартное отклонение. Следовательно, можно сделать вывод, что изменение случайной величины небольшого стандартного отклонения будет иметь большее влияние на значение статистического расстояния, чем изменение случайной величины большого стандартного отклонения. Другими словами, статистическое расстояние — это взвешенное расстояние по прямой линии, где наибольшее значение имеет случайная величина, которая имеет наименьшее стандартное отклонение, чтобы компенсировать расстояние от центра.


До сих пор предполагалось, что случайные величины нескоррелированные.
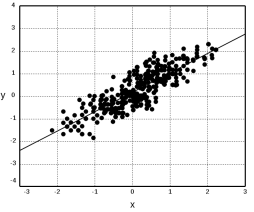
Теперь предположим, что это не так. На рисунке ![]() показан случай положительно скоррелированных случайных величин. Чтобы получить статистическое расстояние, давайте в этом случае обобщим формулу
показан случай положительно скоррелированных случайных величин. Чтобы получить статистическое расстояние, давайте в этом случае обобщим формулу ![]() . Мы знаем, что общее уравнение эллипса задается следующим образом:
. Мы знаем, что общее уравнение эллипса задается следующим образом:
![]()
где ![]() являются такими постоянными, которые удовлетворяют условию
являются такими постоянными, которые удовлетворяют условию
![]() , а
, а ![]() — фиксированное число.
— фиксированное число.
Выбрав правильные константы
Правильный выбор ![]() приведет к получению формулы для статистического расстояния, когда
приведет к получению формулы для статистического расстояния, когда ![]() и
и ![]() скоррелированы. Формула выглядит следующим образом:
скоррелированы. Формула выглядит следующим образом:
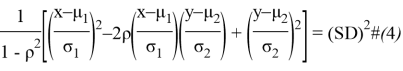
где ![]()
![]() является коэффициентом корреляции между
является коэффициентом корреляции между ![]() и
и ![]() .
.
Когда случайные величины ![]() и
и ![]() не скоррелированы, то есть
не скоррелированы, то есть ![]() , формула
, формула ![]() принимает вид
принимает вид ![]() , а полученный эллипс принимает вид что на рисунке
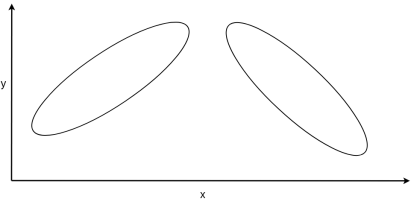
, а полученный эллипс принимает вид что на рисунке ![]() . Когда
. Когда ![]() , то полученный эллипс будет наклонен влево, а когда
, то полученный эллипс будет наклонен влево, а когда ![]() , то эллипс будет наклонен вправо (рис. 5).
, то эллипс будет наклонен вправо (рис. 5).
![]()
Формула ![]() может быть представлена в виде матрицы следующим образом:
может быть представлена в виде матрицы следующим образом:
![]()
где ![]() ,
, ![]() , а матрица
, а матрица ![]() является обратной матрицы
является обратной матрицы 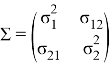 , где
, где ![]() является ковариацией между
является ковариацией между ![]() и
и ![]() . Матрицу
. Матрицу ![]() называют матрицей ковариацией случайных величин.
называют матрицей ковариацией случайных величин.
Полученную формулу ![]() можно обобщить для того случая, когда
можно обобщить для того случая, когда![]() является
является ![]() — мерным случайным вектором,
— мерным случайным вектором, ![]() вектором средних, а
вектором средних, а
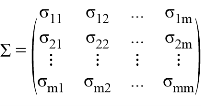
![]()
В дальнейшем мы увидим, что матричные виды ![]() и
и ![]() являются различными представлениями статистики Хотеллинга
являются различными представлениями статистики Хотеллинга ![]() .
. ![]()
Статистика ![]() стьюдента иее обобщение статистика
стьюдента иее обобщение статистика ![]() Хотеллинга
Хотеллинга
Статистика ![]() Стьюдента вычисляется для случайно выбранной
Стьюдента вычисляется для случайно выбранной ![]() выборки из нормально распределенной генеральной совокупности, которая имеет
выборки из нормально распределенной генеральной совокупности, которая имеет ![]() средную и
средную и ![]() дисперсии. Это статистика дана следующим образом:
дисперсии. Это статистика дана следующим образом:
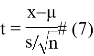
где
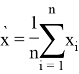
среднее значение выборок, а ՝
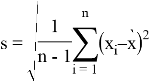
стандартные отклонения для выборок.
Квадрат
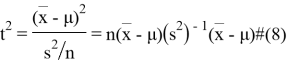
И полученное значение будет квадратом статистического расстояния между выборковым средним и средним генеральной совокупности.
В формуле ![]() числитель — это квадрат Евклидова расстояния между
числитель — это квадрат Евклидова расстояния между ![]() и
и ![]() , то есть это является величина близости среднего значения выборок и среднего значения генеральной совокупности. Когда
, то есть это является величина близости среднего значения выборок и среднего значения генеральной совокупности. Когда ![]() приближается к
приближается к ![]() , значение
, значение ![]() приближается к нулю. Разделив квадрат Евклидова расстояния на дисперсию
приближается к нулю. Разделив квадрат Евклидова расстояния на дисперсию ![]() , то есть на
, то есть на ![]() , мы получим квадрат упомянутого статистического расстояния. Хотеллинг обобщил одномерную
, мы получим квадрат упомянутого статистического расстояния. Хотеллинг обобщил одномерную ![]() статистику на многомерную
статистику на многомерную ![]() статистику, которая основана на значении, полученных из выборочных ковариационных матриц. Это выглядит так:
статистику, которая основана на значении, полученных из выборочных ковариационных матриц. Это выглядит так:
Предположим, у нас есть ![]() –ое количество выборок:
–ое количество выборок: ![]() где
где ![]() взяты из
взяты из ![]() -мерного нормального распределения, у которой есть
-мерного нормального распределения, у которой есть ![]() вектор средних и матрица ковариаций
вектор средних и матрица ковариаций ![]() . Многомерное обобщение статистики Стьюдента
. Многомерное обобщение статистики Стьюдента ![]() Хотеллинга имеeт следующий вид:
Хотеллинга имеeт следующий вид:
![]()
где ![]() и
и ![]() являются выброчними величинами
являются выброчними величинами ![]() и
и ![]() и имеют следующий вид:
и имеют следующий вид: ![]()
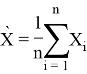
и
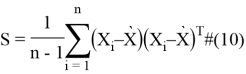
Для выборок ![]() матрица ковариаций может быть представлена также в следующем виде:
матрица ковариаций может быть представлена также в следующем виде:

где ![]() является
является ![]() -ой выборочной дисперсией случайной величины, а
-ой выборочной дисперсией случайной величины, а ![]() является выборочной ковариацией между
является выборочной ковариацией между ![]() -ой и
-ой и ![]() -ой случайными величинами.
-ой случайными величинами.
Применение
В следующем примере мы применим Хотеллинг T2. Предположим, что исследование было проведено среди ![]() человек в возрасте
человек в возрасте ![]() лет и были собраны данные об использовании следующих
лет и были собраны данные об использовании следующих ![]() ингридиентов в их ежедневном рационе: кальций, железо, протеин, витамин
ингридиентов в их ежедневном рационе: кальций, железо, протеин, витамин ![]() и витамин
и витамин ![]() . В таблице покажем суточное количество, необходимую норму для каждого ингридиента и полученные средние данные․
. В таблице покажем суточное количество, необходимую норму для каждого ингридиента и полученные средние данные․
|
Ингредиент |
Необходимая норма |
Среднее |
|
Кальций |
1000 мг |
624.0 мг |
|
Железо |
15 мг |
11.1 мг |
|
Протеин |
60 г |
65.8 г |
|
Витамин |
800 |
839.6 |
|
Витамин |
75 мг |
78.9 мг |
Таблица 1
Суточная необходимая норма иполученные средние данные для каждого ингридиента ![]()
Наша задача — выяснить, принимают ли люди необходимую суточную дозу или нет. Прежде чем делать расчеты, давайте представим следующие идеи.
Нулевая гипотеза — статистическая гипотеза согласно которому характеристика описивающий генеральную совокупность не меняется. ![]()
Альтернативная гипотеза — противоположное предположение нулевой гипотезе. ![]()
Случайная величина ![]() имеет
имеет ![]() -распределение по степени свободы
-распределение по степени свободы ![]() и
и ![]() , если ее функция плотности задана следующим образом:
, если ее функция плотности задана следующим образом:
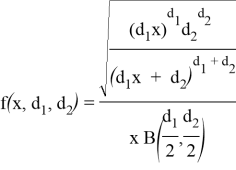
где
![]() статистика представляется
статистика представляется ![]() статистикой следующим образом.
статистикой следующим образом.
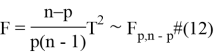
где ![]() и
и ![]() являются степенями свободы.
являются степенями свободы.
![]()
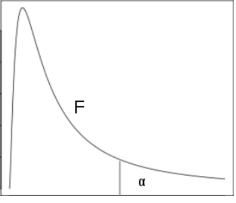
Рис.6. показывает значения распределения плотности ![]() в случаях разных степеней свободы. Значение, соответствующее
в случаях разных степеней свободы. Значение, соответствующее ![]() и выбранной степени свободы, представляет собой значение плотности распределения
и выбранной степени свободы, представляет собой значение плотности распределения ![]() , правая часть которого имеет поверхность
, правая часть которого имеет поверхность ![]() (рис. 6).
(рис. 6).
Мы отвергнем нулевую гипотезу ![]() на уровне
на уровне ![]() , если статистика
, если статистика ![]() больше критического значения в таблице
больше критического значения в таблице ![]() :
:
![]()
Давайте перейдем к расчетам. В нашем случае нулевая гипотеза состоит в том, что люди принимают все компоненты в необходимом количестве. Нулевая гипотеза будет опровергнута, если окажется, что люди не принимают один из компонентов в необходимом количестве. Математически нулевая гипотеза (![]() ) состоит в том, что вектор средних значений генеральной совокупности
) состоит в том, что вектор средних значений генеральной совокупности ![]() равен вектору средних, полученного из выборок —
равен вектору средних, полученного из выборок — ![]() а альтернативная гипотеза (
а альтернативная гипотеза (![]() ) состоит в том, что они не равны друг другу.
) состоит в том, что они не равны друг другу.
![]()
Для произведения расчетов давайте вспомним вид статистики Хотеллинга
![]()
где
Теперь давайте найдем матрицу ![]() для имеющихся данных,
для имеющихся данных,

Исходя из формулы ![]() статистика
статистика ![]() Хотеллинга будет:
Хотеллинга будет:
![]()
У нас есть степени свободы ![]()
![]() , следовательно, из формулы
, следовательно, из формулы ![]() получаем статистику
получаем статистику ![]() :
:
![]()
Если мы посмотрим на критическое значение для ![]() в таблице
в таблице ![]() , то увидим, что
, то увидим, что ![]() . Оказалось, что значение
. Оказалось, что значение ![]() больше критического значения. Следовательно, мы можем отрицать нулевую гипотезу, которая утверждает, что среднее значение соответствует необходимому рациону.
больше критического значения. Следовательно, мы можем отрицать нулевую гипотезу, которая утверждает, что среднее значение соответствует необходимому рациону.
Вывод: Среднесуточная доза из ![]() компонентов, отобранных для всех людей в возрасте
компонентов, отобранных для всех людей в возрасте ![]() лет, не соответствует желаемой дозе.
лет, не соответствует желаемой дозе.
Литература:
- R. L. Mason, J. C. Young, Multivariate statistical process control with industrial applications, Society for Industrial and Applied Mathematics, 2002
- R. S. Witte, J. S. Witte, Statistics, Eleventh Edition, 2017
- Health Survey // Penn State. URL: https://newonlinecourses.science.psu.edu/stat505/lesson/7/7.1/7.1.1 (дата обращения: 27.04.2020).
Ключевые слова
статистика Хотеллинга, статистическое расстояние, ингридиенты, t статистикаПохожие статьи
Шаблон Excel для проверки законов распределения данных...
В статье рассматривается процедура создания шаблона Excel и опыт его применения для автоматического построения гистограмм и кривых Гаусса по результатам данных экспериментальных наблюдений с одновременной оценкой согласия по критерию Пирсона в...
К вопросу о проверке параметрических статистических гипотез...
В формуле (1) — случайная величина. При условии правильности нулевой гипотезы статистика (1)
случайная величина имеет распределение.
Ключевые слова:выборка, генеральная совокупность, статистические критерии проверки гипотез, параметрические и...
Методы математической статистики в технических исследованиях
Средние величины, характеризуя частотный ряд одним числом, не учитывают разброса признака.
Для нормального распределения эти величины нулевые. Если асимметрия и эксцесс – небольшие величины, это свидетельствует о близости распределения к нормальному.
Проблемы применения статистических критериев проверки...
Ключевые слова:выборка, генеральная совокупность, статистические критерии проверки гипотез, параметрические и непараметрические критерии. Одной из важнейших задач математической статистики на сегодняшний день является разработка и применение...
Статистическая обработка результатов гидравлического...
Если в генеральной совокупности единицы располагаются случайным образом по
В формуле (1) — случайная величина. При условии правильности нулевой гипотезы
При условии правильности нулевой гипотезы статистика (1) имеет распределение, близкое к...
Вычисление статистических показателей с использованием...
При проведении экспериментов или опытов получаются случайные величины, появление которых предсказать невозможно, и они чаще всего подчиняются нормальному закону распределения (закону Гаусса).
Анализ методов распознавания образов | Статья в журнале...
Шкалированное евклидово расстояние между вектором x и вектором математического ожидания равно.
Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами μ и σ^2, если ее плотность вероятности имеет вид
Проверка статистических гипотез в психолого-педагогических...
если Т (статистика критерия) принадлежит области принятия нулевой гипотезы, то нулевая гипотеза принимается, а в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза. В зависимости от задач психолого-педагогического исследования...
Проверка нормальности распределения оценок параметров...
Введение. Работа посвящена применению методов математической статистики к исследованию данных эксперимента с полевыми эмиссионными катодами. Целью работы является проведение анализа оценок сигнала полевой электронной эмиссии с помощью...
Похожие статьи
Шаблон Excel для проверки законов распределения данных...
В статье рассматривается процедура создания шаблона Excel и опыт его применения для автоматического построения гистограмм и кривых Гаусса по результатам данных экспериментальных наблюдений с одновременной оценкой согласия по критерию Пирсона в...
К вопросу о проверке параметрических статистических гипотез...
В формуле (1) — случайная величина. При условии правильности нулевой гипотезы статистика (1)
случайная величина имеет распределение.
Ключевые слова:выборка, генеральная совокупность, статистические критерии проверки гипотез, параметрические и...
Методы математической статистики в технических исследованиях
Средние величины, характеризуя частотный ряд одним числом, не учитывают разброса признака.
Для нормального распределения эти величины нулевые. Если асимметрия и эксцесс – небольшие величины, это свидетельствует о близости распределения к нормальному.
Проблемы применения статистических критериев проверки...
Ключевые слова:выборка, генеральная совокупность, статистические критерии проверки гипотез, параметрические и непараметрические критерии. Одной из важнейших задач математической статистики на сегодняшний день является разработка и применение...
Статистическая обработка результатов гидравлического...
Если в генеральной совокупности единицы располагаются случайным образом по
В формуле (1) — случайная величина. При условии правильности нулевой гипотезы
При условии правильности нулевой гипотезы статистика (1) имеет распределение, близкое к...
Вычисление статистических показателей с использованием...
При проведении экспериментов или опытов получаются случайные величины, появление которых предсказать невозможно, и они чаще всего подчиняются нормальному закону распределения (закону Гаусса).
Анализ методов распознавания образов | Статья в журнале...
Шкалированное евклидово расстояние между вектором x и вектором математического ожидания равно.
Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами μ и σ^2, если ее плотность вероятности имеет вид
Проверка статистических гипотез в психолого-педагогических...
если Т (статистика критерия) принадлежит области принятия нулевой гипотезы, то нулевая гипотеза принимается, а в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза. В зависимости от задач психолого-педагогического исследования...
Проверка нормальности распределения оценок параметров...
Введение. Работа посвящена применению методов математической статистики к исследованию данных эксперимента с полевыми эмиссионными катодами. Целью работы является проведение анализа оценок сигнала полевой электронной эмиссии с помощью...











