В результате психолого-педагогического эксперимента можно получить три типа данных:
– количественные данные- данные получаемые при измерениях (данные о результатах тестирования, весе, размерах и т. п.);
– порядковые данные- данные соответствующие местам этих элементов в последовательности, полученной при их расположении в возрастающем или убывающем порядке;
– качественные данные — данные представляющие собой частоту встречаемости какого-либо свойства в исследуемой группе. (число людей имеющих высшее и средне- специальное образование, сильных и слабых и т. п.).
Задачей анализа полученных данных является изучение частоты встречаемости тех или иных значения признака в эксперименте. Эти данные дают предварительную информацию о виде распределения признака: о том, какие значения встречаются реже, а какие чаще, насколько выражена изменчивость признака. Существуют следующие виды распределения: Равномерное распределение (все значения встречаются одинаково часто), симметричное распределение (одинаково часто встречаются крайние значения), нормальное распределение (крайние значения встречаются редко и частота постепенно повышается от крайних к серединным значениям признака).
В психолого-психологических исследованиях чаще всего ссылаются на нормальное распределение.
Для математической обработки данных выдвигают гипотезы. Гипотезами в педагогических исследованиях является предположение, что одно из средств будет более эффективным, чем другие средства.
Для проверки гипотез выдвигается нулевая гипотеза — это проверяемое предположение. Примером нулевой гипотезы в педагогике является утверждение о том, что различие в результатах выполнения двумя группами учащихся одной и той же контрольной работы вызвано лишь случайными причинами.
Другое проверяемое предположение называется конкурирующей или альтернативной гипотезой.
Проверка нулевой гипотезы в общем случае включает следующие этапы:
- задается допустимая вероятность ошибки первого рода
- выбирается критерий (Т)
- по исходным данным вычисляется значение статистики Т
- если Т (статистика критерия) принадлежит области принятия нулевой гипотезы, то нулевая гипотеза принимается, а в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза.
В зависимости от задач психолого-педагогического исследования, могут быть использованы различные критерии. Классификация задач и методов решения рассмотрена в учебнике Сидоренко Е. В. В представленной ниже таблице представлены ограничения на применение некоторых критериев.
Ограничения критериев
|
Методы |
Ограничения |
||
|
По количеству испытуемых |
По шкале |
Дополнительные показатели |
|
|
G — критерий знаков |
+ |
+ |
|
|
L — критерий тенденций Пейджа. |
+ |
||
|
Однофакторный дисперсионный анализ Фишера. |
+ |
||
|
Q— критерий Розенбаума |
+ |
+ |
|
|
rs — коэффициент ранговой корреляции Спирмена. |
+ |
||
|
S — критерий тенденций Джонкира |
+ |
||
|
U — критерий Манна-Уитни |
+ |
||
|
χ2 — критерий Пирсона хи-квадрат |
+ |
+ |
+ |
|
χл2 — критерий Фридмана |
+ |
||
Часто при обработке данных используется t-критерий Стьюдента.
Исходя из представленной таблицы видно, что при использовании данного критерия необходимо учесть и дополнительные показатели. Таких ограничений два.
- Нормальность распределения количественного признака в обеих сравниваемых группах.
- Равенство генеральных дисперсий в этих группах.
Определить нормальность распределения признака можно с помощью:
1) построения кривой нормального распределения по эмпирическим данным;
2) проверки нормальности распределения результативного признака.
Второе условие, равенство дисперсий в двух группах можно проверить с помощью F критерия Фишера.
Рассмотрим применение критерия Стьюдента на примере:
Пример: В двух группах учащихся, в каждой из которых 16 человек (экспериментальной и контрольной) были получены следующие результаты тестирования по одному и тому же учебному предмету с одинаковым содержанием тестовых материалов (16 вопросов) Можно ли считать, что различие в результатах выполнения двумя группами учащихся тестов определяется влиянием экспериментального обучения?
Экспериментальная группа: 11, 13,12, 9, 10, 11, 8, 10, 15, 14, 8, 7,10,10,5,8
Контрольная группа: 6,10,11,11,10,7,7,5,10,12,8,10,5,5,5,14
Проверим возможности применения критерия Стьюдента:
Нормальность распределения признака для первой группы с помощью построения кривой нормального распределения по эмпирическим данным;
- Отсортируем данные по возрастанию (первый столбец таблицы).
- Подсчитаем частоту повторения каждого значения — m (второй столбец таблицы).
-
Рассчитаем
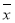 ,σ,
,σ,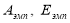 используя статистические функции ЕXCEL.
используя статистические функции ЕXCEL.
-
Находим нормированное отклонение каждого варианта от средней для этого предварительно найдем разность
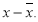 (третий столбец таблицы).
(третий столбец таблицы).
-
Четвертый столбец таблицы заполним с помощью формулы:

-
Для найденных t по определяем
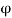 (t).(пятый столбец таблицы)
(t).(пятый столбец таблицы)
-
Рассчитаем константу, для этого найдем
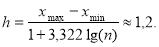
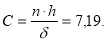
-
Найдем произведение
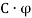 (t) (шестой столбец таблицы). Результаты умножения округлим.
(t) (шестой столбец таблицы). Результаты умножения округлим.
-
По данным
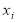 и
и  (первый и последний столбец) построим график.
(первый и последний столбец) построим график.
Таблица 1
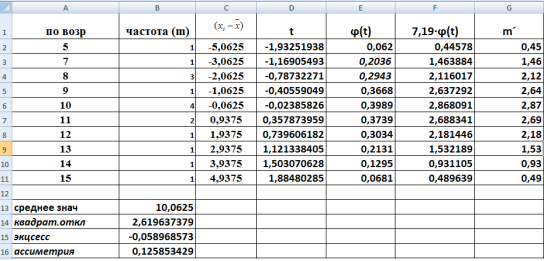
Построим кривую нормального распределения
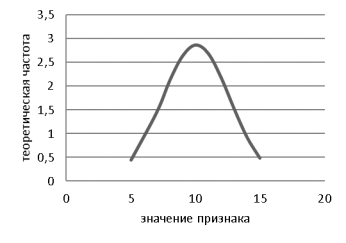
По полученному графику делаем вывод: распределение результативного признака контрольной группе не отличается от нормального.
Проверим нормальность распределения второй выборки с помощью результативного признака:
Рассчитаем характеристики положения:
Рассчитаем критические значения асимметрии и эксцесса по формулам Е. И. Пустыльника:
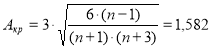
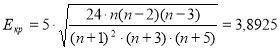
![]()
![]()
Так как эмпирические значения А и Е меньше критических значений, то можно сделать вывод: распределение результативного признака в экспериментальной группе не отличается от нормального.
Равенство генеральных дисперсий в этих группах проверим. с помощью критерия Фишера.
Рассчитав дисперсии для переменных для каждой группы получим:
![]()
![]() ,
, ![]()
По таблице приложений для F критерия при степенях свободы равных
k1 = k2=16–1=15 находим Fкрит=2,4 (>1,14), следовательно, можно утверждать, что Н0 (гипотеза о равенстве дисперсий) принимается на уровне 5 %.
Так как выполнены два условия применим критерий Стьюдента. Проверим гипотезу при уровне значимости Р = 5 %.
Выдвинем гипотезы:
Н0 — различие в результатах выполнения двумя группами учащихся тестов определяется влиянием экспериментального обучения
Н1:. различие в результатах выполнения двумя группами учащихся тестов вызвано лишь случайными причинами.
Вычислим эмпирическое значение критерия
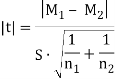 =0,225
=0,225 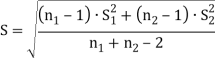 =3,03
=3,03
Определяем критическое значение критерия Стьюдента
![]()
Сопоставив эмпирическое и критическое значения критерия, получаем: ![]() . Нет оснований опровергнуть нулевую гипотезу т. е. различие в результатах выполнения двумя группами учащихся тестов определяется влиянием экспериментального обучения.
. Нет оснований опровергнуть нулевую гипотезу т. е. различие в результатах выполнения двумя группами учащихся тестов определяется влиянием экспериментального обучения.
Литература:
- Ермолаев О. Ю. Математическая статистика для психологов: Учебник / О. Ю. Ермолаев. 2-е изд., исп. М.: Московский психолого-социальный институт: Флинта, 2003. 336 с.
- Сидоренко Е. В. Методы математической обработки в психологии. — СПб.: ООО «Речь», 2003. — 350 с.







